Рассмотрим критерий нильпотентности групп и связь нильпотентной группы со своей подгруппой Фраттини.
Теорема 2.3 (Критерий нильпотентности). 


 .
.
Доказательство.
1) Необходимость. Пусть  ,
,  . Покажем, что
. Покажем, что  .
.
Так как  , то
, то  и
и 

 , а значит
, а значит 

 , следовательно
, следовательно  .
.
2) Достаточность. Пусть  ,
,  . Покажем, что
. Покажем, что  . Пусть
. Пусть 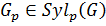 . Покажем, что
. Покажем, что 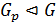 . Достаточно показать, что
. Достаточно показать, что 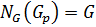 . Допустим, что
. Допустим, что  тогда существует
тогда существует 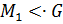 , такая, что
, такая, что  а по лемме 1.2.5 следует, что
а по лемме 1.2.5 следует, что  . Таким образом,
. Таким образом,  следовательно
следовательно  . Получено противоречие. Таким образом,
. Получено противоречие. Таким образом, 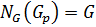 , а значит,
, а значит, 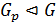 . Отсюда следует, что
. Отсюда следует, что  . Теорема доказана.
. Теорема доказана.
Определение 2.3. Нормальный ряд  группы G называется центральным, если
группы G называется центральным, если 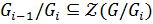 ,
,  .
.
Определение 2.4. Группа  называется нильпотентной, если
называется нильпотентной, если  обладает центральным рядом.
обладает центральным рядом.
Теорема 2.4. Конечная нильпотентная группа является разрешимой.
Доказательство.
Пусть 

 имеет нормальный ряд
имеет нормальный ряд  , где
, где 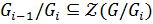 ,
,  . Покажем, что
. Покажем, что 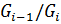 – абелева группа.
– абелева группа.
Так как 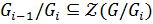 и
и 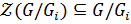 ,
, 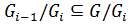 (6). Обозначим
(6). Обозначим 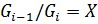 , а
, а  . С другой стороны, так как
. С другой стороны, так как 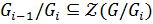 , то есть
, то есть 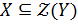 , то
, то  . Но по (6)
. Но по (6)  , значит
, значит  где
где  рассматривается как элемент из
рассматривается как элемент из  . Значит,
. Значит,  – абелева группа. По определению 1.1.22
– абелева группа. По определению 1.1.22  . Теорема доказана.
. Теорема доказана.
Теорема 2.5. (Фраттини). Подгруппа Фраттини конечной группы является нильпотентной.
Доказательство.
Пусть  – конечная группа. Покажем, что
– конечная группа. Покажем, что  . Пусть
. Пусть  .
.
Покажем, что  .
.
Так как  , то по лемме 1.2.4
, то по лемме 1.2.4  , а по теореме 1.2.5
, а по теореме 1.2.5  . По теореме 1.2.6
. По теореме 1.2.6  . По замечанию 1.2.2
. По замечанию 1.2.2  . Следовательно,
. Следовательно,  , а значит
, а значит  , отсюда следует, что
, отсюда следует, что  и
и  . Теорема доказана.
. Теорема доказана.
Теорема 2.6. 1. 

 .
.
2. 

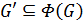 .
.
Теорема 2.7. 1. Пусть 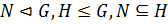 . Если
. Если  , то
, то  .
.
2. Если  , то
, то  .
.
3. Если  , то
, то  .
.
4. Если  , то
, то  .
.
5. Если  и
и  , то
, то  .
.
6. Если  – абелева группа.
– абелева группа.
7.  .
.
Определение 2.5. Пусть  – конечная группа. Наибольшая нормальная нильпотентная подгруппа группы
– конечная группа. Наибольшая нормальная нильпотентная подгруппа группы  называется подгруппой Фиттинга и обозначается
называется подгруппой Фиттинга и обозначается  .
.
Теорема 2.8. (Фиттинга). Пусть  – конечная группа. Тогда произведение всех нормальных нильпотентных подгрупп группы
– конечная группа. Тогда произведение всех нормальных нильпотентных подгрупп группы  является подгруппой Фиттинга то есть в конечных группах подгруппы Фиттинга существуют.
является подгруппой Фиттинга то есть в конечных группах подгруппы Фиттинга существуют.
Лемма 2.1. 1.  – наибольшая нормальная нильпотентная подгруппа группы G.
– наибольшая нормальная нильпотентная подгруппа группы G.
2.  .
.
3. 
Лемма 2.2. 1.  ; если
; если  разрешима и
разрешима и 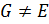 , то
, то  .
.
2.  =
=  .
.
3. Если 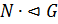 , то
, то  ; если, кроме того,
; если, кроме того, 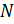 абелева, то
абелева, то  .
.
Теорема 2.9. 1. 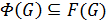 .
.
2. 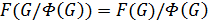 .
.
3. Если  , то
, то  .
.
4. Если 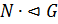 , то
, то  .
.
5.  , где
, где  пробегает все главные факторы группы
пробегает все главные факторы группы  .
.
Теорема 2.10. Пусть  . Если фактор-группа
. Если фактор-группа 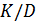 нильпотентна, то
нильпотентна, то  нильпотентна.
нильпотентна.
Теорема 2.11. Группа нильпотентна тогда и только тогда, когда ее коммутант содержится в подгруппе Фраттини.
Определение 2.6. Нильпотентной длиной разрешимой группы  называют наименьшее
называют наименьшее 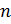 , для которого
, для которого 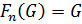 , и обозначают
, и обозначают  .
.
Лемма 2.3. 1. Если  – разрешимая группа, то длина любого нормального ряда группы
– разрешимая группа, то длина любого нормального ряда группы  с нильпотентными факторами не меньше, чем
с нильпотентными факторами не меньше, чем  .
.
2. Нильпотентная длина разрешимой группы совпадает с длиной самого короткого нормального ряда с нильпотентными факторами.
Метанильпотентные группы
Определение 2.7. Если фактор-группа  нильпотентна, то группу
нильпотентна, то группу  называют метанильпотентной.
называют метанильпотентной.
Теорема 2.12. 1. В разрешимой группе подгруппа Фиттинга совпадает с пересечением максимальных подгрупп, не содержащих подгруппу Фиттинга.
2. В разрешимой ненильпотентной группе пересечение максимальных подгрупп, содержащих подгруппу Фиттинга, метанильпотентно.
Доказательство.
Обозначим через  пересечение всех максимальных подгрупп группы
пересечение всех максимальных подгрупп группы  , не содержащих
, не содержащих  , а через
, а через  пересечение максимальных подгрупп группы
пересечение максимальных подгрупп группы  , содержащих
, содержащих  . Ясно, что подгруппы
. Ясно, что подгруппы  и
и  характеристические в группе
характеристические в группе  и
и  .
.
1. В фактор-группе  подгруппа Фиттинга
подгруппа Фиттинга 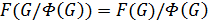 на основании леммы 2.2, поэтому
на основании леммы 2.2, поэтому 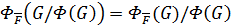 . Предположим, что
. Предположим, что  и
и  – минимальная нормальная подгруппа группы
– минимальная нормальная подгруппа группы  , содержащаяся в
, содержащаяся в  . Так как подгруппа
. Так как подгруппа  нормальна в группе
нормальна в группе  и фактор-группа
и фактор-группа  нильпотентна, то по теореме 2.7 подгруппа K нильпотентна и
нильпотентна, то по теореме 2.7 подгруппа K нильпотентна и  . Но теперь
. Но теперь  , то есть получили противоречие. Поэтому допущение неверно и
, то есть получили противоречие. Поэтому допущение неверно и  , то есть
, то есть 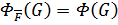 .
.
2. Пусть  – разрешимая нильпотентная группа. Ясно, что
– разрешимая нильпотентная группа. Ясно, что  и
и 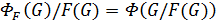 . Поэтому
. Поэтому  метанильпотентна.
метанильпотентна.
Заключение
В данном реферате были выполнены следующие задачи:
1. Рассмотрены определения нильпотентной группы, нильпотентной длины разрешимой группы, подгруппы Фиттинга, центрального ряда группы.
2. Изучены основные свойства нильпотентных групп. Рассмотрен критерий нильпотентности и связь нильпотентных групп с разрешимыми группами. Изучены свойства подгруппы Фитинга и свойство нильпотентности подгруппы Фраттини.
3. Исследована связь метанильпотентных групп с подгруппами Фиттинга конечных нильпотентых групп.
Список используемой литературы
1. Воробьев Н.Н. Алгебра классов конечных групп. Витебск: ВГУ имени П.М. Машерова, 2012.
2. Каргаполов М.И., Мерзляков Ю.И. Основы теории групп. - М.: Наука, 1982.
3. Кострикин А. И. Введение в алгебру. Часть 1. Основы алгебры. - М.: Физико-математическая литература, 2000.
4. Кострикин А.И. Введение в алгебру. Часть 2. Линейная алгебра. - М.: Физико-математическая литература, 2000.
5. Кострикин А.И. Введение в алгебру. Часть 3. Основные структуры алгебры. - М.: Физико-математическая литература, 2000.
6. Курош А.Г. Теория групп. – М.: Физико-математическая литература, 2011.
7. Монахов В.С. Введение в теорию конечных групп и их классов: учебное пособие. – Мн.: Вышэйшая школа, 2006.




