Определение 2.1. Конечная группа  называется нильпотентной, если каждая силовская подгруппа группы
называется нильпотентной, если каждая силовская подгруппа группы  нормальна в
нормальна в  .
.
Определение 2.2. Конечная группа  называется нильпотентной, если
называется нильпотентной, если  является прямым произведением своих силовских подгрупп.
является прямым произведением своих силовских подгрупп.
Через 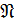 обозначается множество всех конечных нильпотентных групп.
обозначается множество всех конечных нильпотентных групп.
Теорема 2.1 (Свойства нильпотентных групп).
1. Если  ,
,  , то
, то 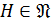 .
.
2. Если  ,
,  , то
, то 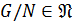 .
.
3. Если 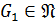 ,
, 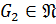 , то
, то 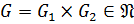 .
.
4. Если 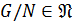 ,
, 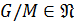 , то
, то 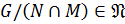 .
.
5. Если  ,
,  , то
, то 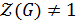 .
.
6. Если  ,
, 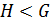 , то
, то 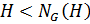 .
.
Доказательство.
1. Пусть  ,
,  . Покажем, что
. Покажем, что 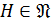 .
.
Пусть 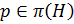

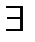
 . Покажем, что
. Покажем, что  . Пусть
. Пусть 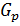 – силовская p -подгруппа в G. Так как
– силовская p -подгруппа в G. Так как  , то
, то 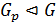 . Следовательно, по теореме 1.2.3(2),
. Следовательно, по теореме 1.2.3(2), 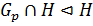 . Достаточно показать, что
. Достаточно показать, что 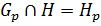 .
.
Так как  – p -подгруппа группы
– p -подгруппа группы 
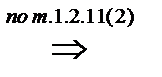
 содержится в некоторой силовской p -подгруппе группы
содержится в некоторой силовской p -подгруппе группы  . Покажем, что
. Покажем, что  Так как по условию теоремы
Так как по условию теоремы  , то
, то 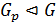 . Согласно определению 1.1.6.
. Согласно определению 1.1.6. 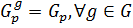 . С другой стороны, по теореме 1.2.11(3): любые две силовские p -подгруппы группы сопряжены, то есть, если
. С другой стороны, по теореме 1.2.11(3): любые две силовские p -подгруппы группы сопряжены, то есть, если 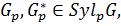 то
то 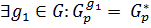 . Но
. Но 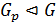 , а, следовательно,
, а, следовательно,  и
и 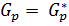 . Значит, если силовская p -подгруппа нормальна в группе, то она совпадает с любой силовской p -подгруппой данной группы. Можно сделать вывод, что нормальная силовская p -подгруппа единственна в группе. Тогда
. Значит, если силовская p -подгруппа нормальна в группе, то она совпадает с любой силовской p -подгруппой данной группы. Можно сделать вывод, что нормальная силовская p -подгруппа единственна в группе. Тогда 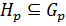 и
и 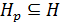
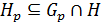 (1) и
(1) и  (2).
(2).
С другой стороны, так как 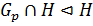 , то
, то 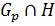 – группа
– группа 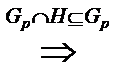
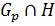 – подгруппа группы
– подгруппа группы 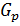 , а по теореме 1.2.1
, а по теореме 1.2.1 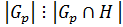 , где
, где 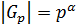
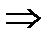
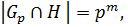 где
где 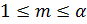
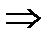
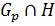 – p -подгруппа группы
– p -подгруппа группы 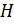 .
.
Таким образом, 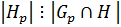 , но
, но  – силовская p -подгруппа
– силовская p -подгруппа 
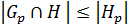
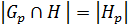 . А по (1)
. А по (1) 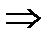
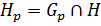 . Следовательно
. Следовательно  , и
, и 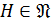 .
.
2. Пусть  ,
,  . Покажем, что то
. Покажем, что то 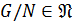
Пусть 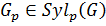 . Так как
. Так как  , то
, то 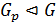
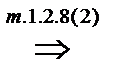
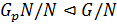 , причем по теореме 1.2.12(2)
, причем по теореме 1.2.12(2) 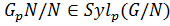 . Тогда
. Тогда 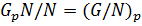
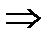
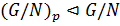
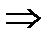
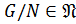 .
.
3. Пусть 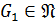 ,
, 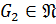 ,
, 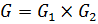 . Покажем, что
. Покажем, что  .
.
Пусть 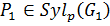 ,
, 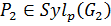 . Так как
. Так как 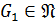 и
и 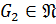 , то
, то  ,
, 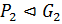 , причем
, причем 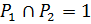 , так как
, так как  . Пусть
. Пусть 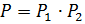 . Покажем, что
. Покажем, что 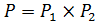 . Для этого необходимо показать, что
. Для этого необходимо показать, что 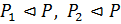 . Так как
. Так как 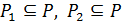 и
и 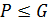 , то по теореме 1.2.3(3) достаточно показать, что
, то по теореме 1.2.3(3) достаточно показать, что 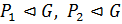 . Покажем, что
. Покажем, что 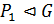 . То есть, покажем что
. То есть, покажем что 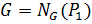 . Так как
. Так как 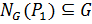 , достаточно показать, что
, достаточно показать, что 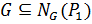 , где по определению 1.1.14
, где по определению 1.1.14 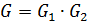 . Для этого достаточно показать, что
. Для этого достаточно показать, что 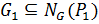 ,
, 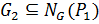 .
.
По условию теоремы 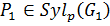 и
и 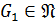
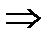

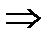
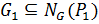 (4). По теореме 1.2.9(1)
(4). По теореме 1.2.9(1)  перестановочны поэлементно
перестановочны поэлементно 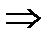
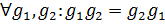 . Значит,
. Значит, 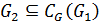 и так как
и так как 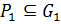 , то
, то 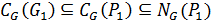 . Таким образом,
. Таким образом,  (5). Из (4) и (5)
(5). Из (4) и (5) 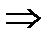
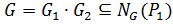
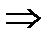
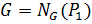 . Следовательно,
. Следовательно,  . Аналогично можно показать, что
. Аналогично можно показать, что 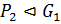 . Из доказанного следует, что
. Из доказанного следует, что 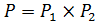 . По теореме 1.2.2
. По теореме 1.2.2  . Так как
. Так как 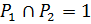
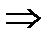
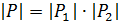 , где
, где  , поскольку
, поскольку 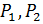 – силовские p -подгруппы. Значит
– силовские p -подгруппы. Значит 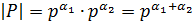
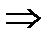
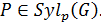 По доказанному,
По доказанному, 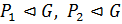
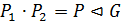
 .
.
4. Пусть 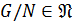 ,
, 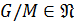 . Покажем, что
. Покажем, что 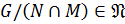 .
.
По теореме 1.2.10 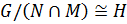 , где
, где 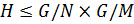 . Так как
. Так как 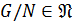 ,
, 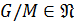
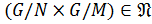
 , а по свойству изоморфных групп
, а по свойству изоморфных групп 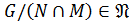 .
.
5. Пусть  ,
,  . Покажем, что
. Покажем, что 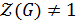 .
.
Пусть 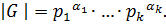 Так как
Так как  , то
, то 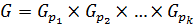

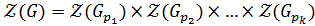 . Так как
. Так как 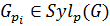 , то
, то  , где
, где 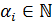 , а значит
, а значит 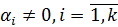 . Таким образом,
. Таким образом, 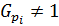 , а по лемме 1.2.2(1)
, а по лемме 1.2.2(1) 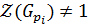 ,
, 
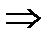
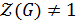 .
.
6. Пусть  ,
, 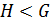 . Покажем, что
. Покажем, что 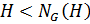 .
.
Допустим, что  – контрпример минимального порядка, то есть
– контрпример минимального порядка, то есть  ,
, 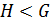 , но
, но 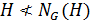 , причем
, причем  – группа наименьшего порядка с таким свойством.
– группа наименьшего порядка с таким свойством.
Рассмотрим 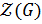 . Так как
. Так как  ,
,  , то
, то 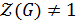 . Возможны 2 случая:
. Возможны 2 случая:
а) Пусть 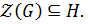 По лемме 1.2.1(1)
По лемме 1.2.1(1) 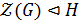 , а значит, существует
, а значит, существует 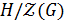 . Так как
. Так как 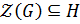 , то
, то 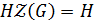 , то по теореме о соответствии
, то по теореме о соответствии 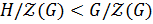 . По следствию 1.2.1
. По следствию 1.2.1 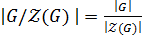 , но так как
, но так как 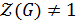 , то
, то 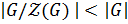


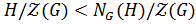
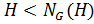 . Получено противоречие.
. Получено противоречие.
б) Пусть 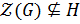 . Тогда,
. Тогда,  . По лемме 1.2.1 так как
. По лемме 1.2.1 так как  , то
, то 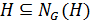 . Так как
. Так как 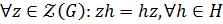 , то
, то 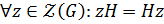
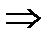
 . Таким образом,
. Таким образом, 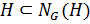 . По условию
. По условию 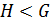 , а по доказанному
, а по доказанному 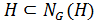
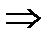
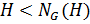 . Получено противоречие.
. Получено противоречие.
Из пунктов а) и б) следует, что контрпримера не существует. Следовательно, теорема верна для любой  .
.
Теорема 2.2. 1. Если  – неединичная нильпотентная группа, то центр
– неединичная нильпотентная группа, то центр 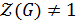 и
и 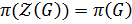 .
.
2. В нильпотентной группе каждая собственная подгруппа отличная от своего нормализатора.
3. В нильпотентной группе  – пересечение неединичной нормальной подгруппы
– пересечение неединичной нормальной подгруппы 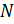 с центром группы отлично от единицы и
с центром группы отлично от единицы и 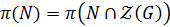 .
.






