Определение 1.1.1. Непустое множество  с определенной на ней бинарной алгебраической операцией
с определенной на ней бинарной алгебраической операцией  называется группой, если выполняются следующие аксиомы (аксиомы группы):
называется группой, если выполняются следующие аксиомы (аксиомы группы):
1) ассоциативность операции  на
на  ;
;
2) 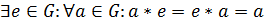 ;
;
3) 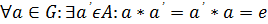 .
.
Определение 1.1.2.
1)Порядком конечной группы  называется число его элементов и обозначается
называется число его элементов и обозначается 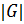 .
.
2)  совокупность всех простых делителей порядка группы
совокупность всех простых делителей порядка группы  , то есть
, то есть  .
.
Определение 1.1.3. Непустое подмножество 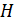 группы
группы  называется подгруппой группы
называется подгруппой группы  и обозначается
и обозначается  , если
, если 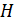 является группой относительно той же операции, что и группа
является группой относительно той же операции, что и группа  .
.
Определение 1.1.4. Пусть  – группа,
– группа,  . Индексом подгруппы
. Индексом подгруппы 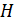 в группе
в группе  называется число смежных классов в разложении группы
называется число смежных классов в разложении группы  по подгруппе
по подгруппе 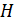 и обозначается
и обозначается  .
.
Определение 1.1.5. Подгруппа 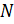 группы
группы  называется нормальной подгруппой и обозначается
называется нормальной подгруппой и обозначается  , если выполняется такое равенство
, если выполняется такое равенство  ,
, 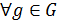 .
.
Определение 1.1.6. Подгруппа 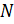 группы
группы  называется нормальной, если
называется нормальной, если 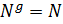 ,
, 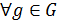 .
.
Определение 1.1.7. Нормальная подгруппа 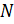 группы
группы  называется минимальной нормальной подгруппой, если
называется минимальной нормальной подгруппой, если 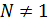 и
и 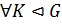 справедливо: если
справедливо: если  , то
, то  или
или 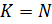 и обозначается
и обозначается 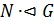 . Другими словами, не существует такой нормальной подгруппы
. Другими словами, не существует такой нормальной подгруппы  группы
группы  , чтобы
, чтобы  .
.
Определение 1.1.8. Пусть  группа,
группа,  . Подгруппой
. Подгруппой  порожденной множеством
порожденной множеством  , называется пересечение всех подгрупп группы
, называется пересечение всех подгрупп группы  , содержащих множество
, содержащих множество  , и обозначается
, и обозначается 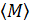 , то есть
, то есть 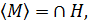 где
где 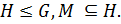
Определение 1.1.9. Подгруппа  группы
группы  называется максимальной подгруппой группы
называется максимальной подгруппой группы  и обозначается
и обозначается  , если
, если  и
и 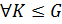 справедливо: если
справедливо: если 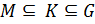 , то
, то  или
или 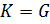 .
.
Другими словами,  , если
, если  и не существует такой подгруппы
и не существует такой подгруппы  группы
группы  , что
, что  .
.
Определение 1.1.10. Подгруппой Фраттини группы  называется пересечение всех максимальных подгрупп группы
называется пересечение всех максимальных подгрупп группы  , если они существуют, и сама группа
, если они существуют, и сама группа  в противном случае и обозначается
в противном случае и обозначается 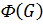 , то есть
, то есть 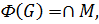 где
где  или
или  .
.
Определение 1.1.11. Пусть  группа,
группа, 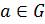 . Элемент
. Элемент 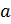 называется необразующим (непорождающим) элементом группы
называется необразующим (непорождающим) элементом группы  , если из
, если из  всегда следует, что
всегда следует, что  .
.
Определение 1.1.12. 1) Элемент 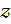 группы
группы  называется центральным элементом группы
называется центральным элементом группы  , если он перестановочен с каждым элементом группы
, если он перестановочен с каждым элементом группы  , то есть
, то есть  .
.
2) Центром группы  называется множество всех центральных элементом группы
называется множество всех центральных элементом группы  и обозначается
и обозначается  , то есть
, то есть 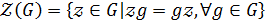 .
.
Определение 1.1.13. Пусть  – группы. Множество
– группы. Множество  относительно покоординатного умножения элементов является группой, которая называется внешним прямым произведением групп
относительно покоординатного умножения элементов является группой, которая называется внешним прямым произведением групп 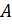 и
и 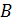 .
.
Определение 1.1.14. Группа  удовлетворяющая трём условиям:
удовлетворяющая трём условиям:
1) 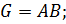
2) 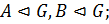
3) 
называется внутренним прямым произведением подгрупп 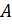 и
и 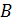 , и обозначается
, и обозначается
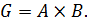
Определение 1.1.15. Пусть  – группа.
– группа.
1) Нормализатором подмножества 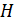 в группе
в группе  называется множество всех элементов группы
называется множество всех элементов группы  , перестановочных с
, перестановочных с 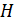 в целом и обозначается
в целом и обозначается  , то есть
, то есть 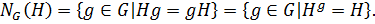
2) Централизатором подмножества 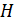 в группе
в группе  называется множество всех элементов группы
называется множество всех элементов группы  , перестановочных с
, перестановочных с 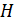 поэлементно и обозначается
поэлементно и обозначается 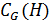 , то есть
, то есть 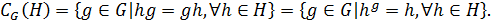
Определение 1.1.16. Группа  называется примарной, если её порядок равен степени некоторого простого числа.
называется примарной, если её порядок равен степени некоторого простого числа.
Определение 1.1.17. Пусть  Группа
Группа  называется -группой, если
называется -группой, если  , где
, где 
Определение 1.1.18. 1) Пусть 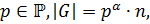 где
где 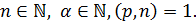 Подгруппа
Подгруппа  группы
группы  называется силовской -подгруппой группы
называется силовской -подгруппой группы  (
(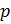 -силовской, силовой), если
-силовской, силовой), если 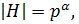 и обозначается
и обозначается 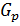 .
.
2)  - множество всех силовских -подгрупп группы
- множество всех силовских -подгрупп группы  .
.
Определение 1.1.19. 1) Конечная последовательность подгрупп группы  вида
вида  (1) называется рядом группы
(1) называется рядом группы  .
.
2) Конечная последовательность подгрупп группы  вида
вида 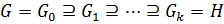 (2) называется цепью группы
(2) называется цепью группы  , соединяющей
, соединяющей  с
с 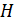 , или
, или  - цепью.
- цепью.
3) Число  называется длиной ряда (1) или цепи (2). Подгруппы
называется длиной ряда (1) или цепи (2). Подгруппы  называются членами ряда (1) или цепи (2).
называются членами ряда (1) или цепи (2).
Определение 1.1.20. 1) Ряд (цепь) группы  называется нормальным рядом (цепью), если
называется нормальным рядом (цепью), если  .
.
2) Ряд (цепь) группы  называется субнормальным рядом (цепью), если
называется субнормальным рядом (цепью), если  .
.
3) Факторгруппы 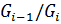 нормального (субнормального) ряда называются нормальными (субнормальными) факторами группы
нормального (субнормального) ряда называются нормальными (субнормальными) факторами группы  .
.
Определение 1.1.21. 1) Нормальный ряд группы  без повторений членов называется главным рядом группы
без повторений членов называется главным рядом группы  , если он не допускает дальнейшего уплотнения нормальными подгруппами, т.е.
, если он не допускает дальнейшего уплотнения нормальными подгруппами, т.е.  .
.
2) Субнормальный ряд группы  без повторений членов называется композиционным рядом группы
без повторений членов называется композиционным рядом группы  , если он не допускает дальнейшего уплотнения субнормальными подгруппами, т.е.
, если он не допускает дальнейшего уплотнения субнормальными подгруппами, т.е.  .
.
3) Фактор главного (композиционного ряда) называется главным (композиционным) фактором.
Определение 1.1.22. Конечная группа  называется разрешимой, если
называется разрешимой, если  обладает нормальным рядом с абелевыми факторами.
обладает нормальным рядом с абелевыми факторами.
Определение 1.1.23. Конечная группа  называется разрешимой, если
называется разрешимой, если  обладает главным рядом с абелевыми факторами.
обладает главным рядом с абелевыми факторами.
Определение 1.1.24. Конечная группа  называется разрешимой, если
называется разрешимой, если  обладает композиционным рядом с факторами простого порядка.
обладает композиционным рядом с факторами простого порядка.
Определение 1.1.25. 1) Группа  называется разрешимой, если
называется разрешимой, если 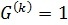 для некоторого
для некоторого 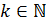 , то есть если ряд коммутантов группы
, то есть если ряд коммутантов группы  обрывается на единичной подгруппе.
обрывается на единичной подгруппе.
2) 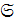 — множество всех разрешимых групп.
— множество всех разрешимых групп.
Используемые результаты
Теорема 1.2.1 (Лагранжа). Порядок подгруппы конечной группы делит порядок группы, то есть  – конечная группа,
– конечная группа,  , то
, то 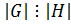 .
.
Следствие 1.2.1. Пусть 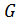 - конечная группа и
- конечная группа и 
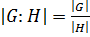 .
.
Теорема 1.2.2 (Теорема о мощности произведения подгрупп). Пусть  – конечная группа,
– конечная группа, 
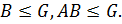 Тогда
Тогда 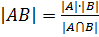 .
.
Теорема 1.2.3 (Свойства нормальных подгрупп).
Пусть  – группа, тогда справедливы следующие утверждения:
– группа, тогда справедливы следующие утверждения:
1) Если 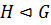 ,
, 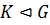 , то
, то  и
и 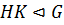 , то есть пересечение нормальных подгрупп есть нормальная подгруппа и произведение нормальных подгрупп есть нормальная подгруппа;
, то есть пересечение нормальных подгрупп есть нормальная подгруппа и произведение нормальных подгрупп есть нормальная подгруппа;
2) Если 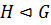 ,
,  , то
, то  , то есть пересечение нормальной подгруппы с произвольной нормальна в произвольной;
, то есть пересечение нормальной подгруппы с произвольной нормальна в произвольной;
3) Если 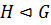 ,
,  и
и 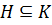 , то
, то 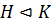 , то есть нормальная подгруппа является нормальной в любой подгруппе ее содержащей.
, то есть нормальная подгруппа является нормальной в любой подгруппе ее содержащей.
Теорема 1.2.4 (О факторгруппе). Пусть  – группа,
– группа,  . Совокупность
. Совокупность 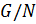 (читается
(читается  по
по 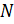 ) всех смежных классов группы
) всех смежных классов группы  по подгруппе
по подгруппе 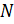 является мультипликативной группой относительно умножения, заданного по правилу:
является мультипликативной группой относительно умножения, заданного по правилу:  выполняется
выполняется 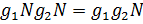 (1), которая называется факторгруппой группы
(1), которая называется факторгруппой группы  по подгруппе
по подгруппе 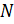 .
.
Замечание 1.2.1. 

 .
.
Теорема 1.2.5. Пусть  – группа,
– группа, 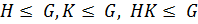 . Тогда
. Тогда 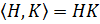 .
.
Теорема 1.2.6 (О строении подгруппы Фраттини). Подгруппа Фраттини группы  состоит из всех необразующих элементов группы
состоит из всех необразующих элементов группы  .
.
Замечание 1.2.2. Если  , то
, то  .
.
Теорема 1.2.7 (О соответствии). Пусть  – группа,
– группа, 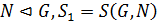 – совокупность всех подгрупп группы
– совокупность всех подгрупп группы  , содержащих
, содержащих 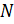 ,
, 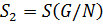 - совокупность всех подгрупп группы
- совокупность всех подгрупп группы 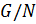 . Тогда между множествами
. Тогда между множествами  и
и 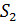 существует взаимно-однозначное соответствие (биекция), причём
существует взаимно-однозначное соответствие (биекция), причём  .
.
Теорема 1.2.8 (О соответствии). Пусть  . Тогда:
. Тогда:
1)  ;
;
2)  ;
;
3)  ;
;
4)  .
.
Теорема 1.2.9. Пусть 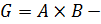 внутреннее прямое произведение.
внутреннее прямое произведение.
Тогда справедливы следующие утверждения:
1) Подгруппы 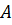 и
и  группы
группы  перестановочны поэлементно, то есть
перестановочны поэлементно, то есть 
2) Каждый элемент 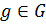 допускает единственное представление в виде
допускает единственное представление в виде
 , где
, где 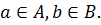
Теорема 1.2.10 (Ремака). Если группа  содержит нормальные подгруппы
содержит нормальные подгруппы  и
и 
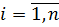 , то группа
, то группа  изоморфна подпрямому произведению групп
изоморфна подпрямому произведению групп 
Лемма 1.2.1. Пусть  – группа. Тогда справедливы следующие утверждения:
– группа. Тогда справедливы следующие утверждения:
1) 
2) 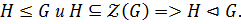
Теорема 1.2.11 (Силова). 1. Пусть  – группа,
– группа,  Тогда в
Тогда в  существуют силовские р -подгруппы.
существуют силовские р -подгруппы.
2. Тогда всякая р -подгруппа группы  содержится в некоторой силовской р -подгруппе группы
содержится в некоторой силовской р -подгруппе группы 
3. Любые 2 силовские p -подгруппы группы 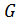 сопряжены в
сопряжены в 
4. Число силовских р -подгрупп группы  сравнимо с единицей по модулю
сравнимо с единицей по модулю 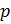 и делит
и делит 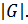
Лемма 1.2.2 (Свойства примарных групп). Пусть  – примарная группа.
– примарная группа.
1. Центр неединичной примарной группы отличен от 1, т.е. если 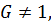 то
то 
2. Если  то
то  , то есть каждая собственная подгруппа примарной группы собственно содержится в своем нормализаторе.
, то есть каждая собственная подгруппа примарной группы собственно содержится в своем нормализаторе.
3. Если  , то
, то 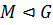 и
и 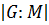 – простое число, то есть все максимальные подгруппы примарной группы нормальны в
– простое число, то есть все максимальные подгруппы примарной группы нормальны в  и имеют простые индексы.
и имеют простые индексы.
4. Если 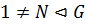 , то
, то  .
.
5. Если 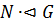 ,
, 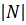 – простое число и
– простое число и 
Теорема 1.2.12. Пусть  Тогда справедливы следующие утверждения:
Тогда справедливы следующие утверждения:
1) 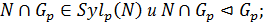
2) 
3) 
Лемма 1.2.3. Пусть  Если
Если  – абелева группа и
– абелева группа и 
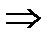
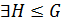 , такая что
, такая что  .
.
Лемма 1.2.4 (Фраттини). Пусть 
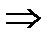

Лемма 1.2.5. Пусть  и
и 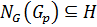
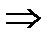

Лемма 1.2.6. Пусть  Тогда
Тогда 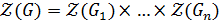 .
.
Лемма 1.2.7. Пусть  – группа,
– группа, 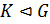 . Тогда
. Тогда 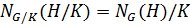 .
.






