Методы исследования устойчивости систем

Гипотеза прямых нормалей

 

В современном строительстве пластинчатые конструкции име­ют большое распространение. Элементами этих конструкций являются не стержни, а пластинки, которые могут работать как в своей плоскости, так и из плоскости. К пластинчатым конструкциям относятся перекрытия, стены, а также коробчатые системы, образующие основную несущую конструкцию здания, в которой стены и перекрытия работают как единая простран­ственная система. К пластинчатым конструкциям примыкают также системы, где элементами являются и стержни и пластинки, как, например, несущая конструкция каркасно-панельных зданий.

Элементом пластинчатых конструкций является пластинка, подчиняющаяся в своей работе гипотезе прямых нормалей. Эта гипотеза формулируется следующим образом: нормаль к перво­начально плоской срединной поверхности пластинки после дефор­мации последней переходит в нормаль к искривленной поверхности. Тем самым постулируется отсутствие сдвигов по плоскостям, параллельным срединной поверхности. Гипотеза прямых нор­малей сводит задачу расчета пластинки из трехмерной в двухмер­ную, так как, согласно этой гипотезе, все слои пластинки деформируются подобно срединной поверхности.

Ввиду симметрии относительно срединной поверхности работу пластинки можно разделить на две независимые части:

1) работу в своей плоскости, при которой происходят перемещения и и v, параллельные срединной плоскости, вдоль координатных осей х и у при отсутствии перемещений w вдоль оси z, нормальной к осям х и у;

2) работу пластинки из плоскости, когда точки срединной поверхности испытывают только перемещения w.

 

Основные положения теории оболочек

 

Большинство элементов инженерных конструкций в расчетной схеме, подлежащих расчету на прочность, как это уже было от­мечено, связаны с расчетом бруса, пластинок или оболочек.

Под оболочкой понимается тело, одно из измерений которого (толщина) значительно меньше двух других. Геометрическое место точек, равноотстоящих от обеих поверхностей оболочки, носит наз­вание срединной поверхности.

Если срединная поверхность оболочки является плоскостью, то такую оболочку называют пластиной.

Геометрическая форма объектов, которые могут быть причислены к оболочкам или пластинам, чрезвычайно разнообразна: в машино­строении — это корпуса всевозможных машин; в гражданском и промышленном строительстве — покрытия и перекрытия, навесы, карнизы; в кораблестроении — корпуса судов, сухих и плавучих до­ков; в авиастроении — фюзеляжи и крылья самолетов; в подвижном составе железнодорожного транспорта, кузова вагонов, цистерны, не­сущие конструкции локомотивов; в атомной энергетике — защитная конструкция атомных станций, корпуса реакторов и т.д.

Если срединная поверхность оболочки образует поверхность вращения в форме цилиндра, то оболочку называют цилиндриче­ской.

К схеме осесимметричной цилиндрической оболочки сво­дится очень много инженерных конструкций, в том числе котлов, баков, нефтепроводов, газопроводов, деталей машин и др.

Задача о расчете тонкостенных оболочек вращения наиболее просто решается в том случае, когда возможно принять, что напря­жения, возникающие в оболочке, постоянны по толщине и, следо­вательно, изгиб оболочки отсутствует.

Теория оболочек, построенная в этом предположении, называ­ется безмоментной теорией оболочек.

 

 

 

 

Если оболочка имеет резкий переход и жесткие защемления и, кроме того, нагружена сосредоточенной силой и моментами, то в местах крепежа оболочки, резких изменений формы, и в местах действия сосредоточенных сил и моментов возникают интенсивные напряжения, обусловленные изгибным эффектом. Учет изгибных эффектов можно получить в рамках моментной теории оболочек.

Следует отметить, что чем меньше отношение толщины h обо­лочки к ее радиусу R, тем точнее выполняется предположение о по­стоянстве напряжений по толщине и тем более точнее выполняются расчеты по безмоментной теории.

Отметим, что оболочка считается тонкой, если h / R< 1/20.

Следовательно, при расчете на прочность тонких оболочек в за­висимости от характера распределения внешних нагрузок, опорных закреплений, применяется или безмоментная или моментная тео­рия. При этом предполагается равномерное распределение на­пряжений по продольным и поперечным сечениям оболочек (от­сутствие в этих сечениях изгибающих, крутящих моментов и попе­речных сил).

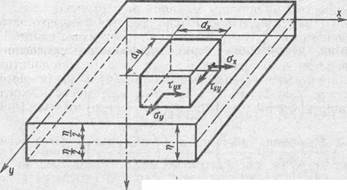
При осесимметричной нагрузке отсутствуют также сдвигающие силы. Определение усилий по безмоментной теории производится достаточно точно на расстоянии, превышающем величину (3 ÷ 5) 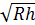от мест скачкообразного изменения формы или площади сечения, жестких контурных закреплений или от места приложения внешних сосредоточенных сил и моментов. Вблизи указанных мест возникают дополнительные напряжения от изгибного эффекта.

В моментной и безмоментной теории тонких оболочек или, так называемой, технической теории оболочек, состоящей в рез­ком различии их толщины и габаритных размеров, влечет за собой возможность упрощения теории путем некоторой схематизации действительной работы конструкций. Эта схематизация формирует­ся в используемых гипотезах, аналогичных гипотезам в теории стержней, т.е. гипотезам плоских сечений и гипотезам «ненадавли­вания» слоев оболочки друг на друга.

Эти гипотезы позволяют свести трехмерную задачу механики сплошной среды к двумерной, подобно тому, как в теории стержней трехмерная задача сведена к одномерной.

Далее в технической теории тонких оболочек пренебрегают членами h/R по сравнению с единицей.

Оболочки, к которым применимы упомянутые выше гипотезы, называются тонкими, а те, к которым эти гипотезы не примени­мы, называются толстыми.

Граница между тонкими и толстыми оболочками условна и оп­ределяется отношением .

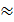
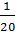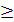
В тех случаях, когда 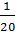для получения приемлемых результатов по точности применяется аппарат механики сплошной среды, в частности теории упругости или пластичности в зависи­мости от постановки задачи.

Рассмотрим расчет пластины постоянной толщины h при дейст­вии внешних сил, перпендикулярных срединной плоскости и сим­метрично расположенными относительно оси z

 

 

 

 

Рис. 1 Рис. 2

 

 

В данном случае функции деформации, перемещения и напря­жения, возникающие в пластине, будут также симметричны относи­тельно оси Z.

Прогиб пластины w и угол поворота нормали v = – dw/ dr являются функциями только от радиуса г (рис. 2).

Из деформированной схемы следует, что точки, распо­ложенные на нормали после изгиба образуют нормаль, совершая поворот на угол v.

Когда пластинка загружена в своей плоскости, все слои ее испытывают одинаковое напряженно-деформированное состояние. Если же пластинка нагружена обратносимметрично, т.е. из своей плоскости, то плоское напряженно-деформированное состояние слоев, оставаясь качественно неизменным, увеличивается пропорционально расстоянию от срединной поверхности. Это следует из гипотезы прямых нормалей.

Кроме изгибающих моментов и крутящих моментов в пластинке возникают поперечные силы, как следствие касательных напряжений.

Заметим, что гипотеза прямых нормалей постулирует отсутствие сдвигов по плоскостям действия этих напряжений. На самом деле эти сдвиги имеются, но они настолько малы, что их влиянием на остальные деформации и перемещения пластинки можно пренебречь. Для соблюдения строгости расчетной схемы следует положить, что мо­дуль сдвига пластинки в плоскостях xz и ху равен бесконечности. Тогда появление касательных напряжений при отсутствии сдвигов оказывается возможным. Точно так же в расчетной схеме пластинки считается, что модуль упругости материала в направлении оси z равен бесконечности, что обеспечивает неизменяемость рас­стояний между слоями пластинки по ее толщине.

 

 

 

Рис. 3

 

 

Таким образом, в технической теории расчета пласти­нок материал считается не изотропным, а обла­дающим в определен­ных направлениях бес­конечно большей жест­костью. В этом отноше­нии теория расчета пла­стинок идентична технической теории рас­чета балок, где наличие касательных напряже­ний в сечении сочетается с гипотезой плоских сечении, исключающей наличие сдвигов.

Необходимость касательных напряжений при составлении условий равновесия бесконечно малого элемента пластинки dxdу, когда приходится вводить поперечные силы Q_x и Q_y на срезах пластинки (рис. 3).

-