Элементы теории устойчивости
Общие положения
Устойчивость сжатых стержней рассматривалась в курсе сопротивления материалов. Там были получены формулы для критической нагрузки сжатого стержня при различных вариантах закрепления его концов.

Рис. 1
При μ =1 Ркр = 
μ =2 Ркр = 
μ =0,7 Ркр = 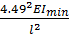
μ =0,5 Ркр = 
Общая формула для критической нагрузки сжатого стержня
Как видно, можно записать общую формулу для критической нагрузки:
Ркр =  ,
,
где v – параметр устойчивости.
Эта формула применяется при расчете рам на устойчивость.
Основные допущения, принимаемые при расчете рам на устойчивость:
1. Действующая на раму нагрузка является узловой.
2. Стержни рамы являются нерастяжимыми и несжимаемыми.
3. Считается, что расстояние между концами стержня при его изгибе не меняется.
Расчет рам на устойчивость удобнее производить методом перемещений.
Основная система и канонические уравнения
Метода перемещений при расчете рам на устойчивость
Основная система метода перемещений при расчете на устойчивость образуется так же, как и при расчете на прочность: сначала определяется степень кинематической неопределимости рамы, а затем ставятся дополнительные связи, число которых равно степени кинематической неопределимости.

Действующая узловая нагрузка не вызывает изгиба стержней рамы. При увеличении нагрузки в некоторый момент произойдет потеря устойчивости: стержни рамы изогнутся, а ее жесткие узлы переместятся.
Линейные и угловые перемещения жестких узлов рамы при потере устойчивости принимаются за неизвестные при расчете на устойчивость методом перемещений.
Канонические уравнения метода перемещений при расчете на устойчивость записываются так же, как и при расчете на прочность, но с одним отличием.
Узловая нагрузка не вызывает реакции в дополнительных связях, поэтому свободные члены канонических уравнений будут равны нулю.
Канонические уравнения метода перемещений при расчете на устойчивость:
r11Z1 + r12Z2 +... + rlnZn = 0
r21Z1 + r22Z2 +... + r2nZn = 0
......................
rn1Z1 + rn2Z2 +... + rnnZn = 0
Определение коэффициентов канонических уравнений с помощью специальных таблиц
Коэффициенты канонических уравнений определяются в общем так же, как и при расчете на прочность. Предварительно должны быть построены единичные эпюры. Эти эпюры строятся с помощью специальных таблиц. В этих таблицах приведены эпюры изгибающих моментов и опорные реакции для сжато-изогнутых стержней.
Эпюры изгибающих моментов будут криволинейными – следствие влияния сжимающей продольной силы на изгибающий момент.
𝜑1(v) учитывает влияние сжимающей продольной силы. Значение этой и других функций приведены в таблице метода перемещений при расчете на устойчивость.
rij = rji.






