Для обработки первичных данных был применен метод математической обработки коэффициента ранговой корреляции Ч.Э. Спирмена с целью доказательства связи между эмоциональным интеллектом и показателем по шкале поддержки теста «САТ». Коэффициент ранговой корреляции Спирмена – это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами чисел.
Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы:
1) Ранжирование значений А и В. Их ранги занесены в колонки «Ранг А» и «Ранг В»;
2) Произвести подсчет разности между рангами А и В (колонка d);
3) Возведение каждой разности d в квадрат (колонка d2);
4) Подсчитать сумма квадратов;
5) Произвести расчет коэффициента ранговой корреляции rs по формуле:
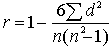(1)
где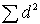 
- сумма квадратов разностей рангов, а 
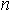- количество испытуемых.
6) Определить критические значения. Если эмпирическое значение превышает критическое значение или равно ему, корреляция достоверно отличается от нуля.
При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками,
- считая значения коэффициента равные 0,64 и менее, показателями слабой тесноты связи;
- значения более 0,64, но менее 0,79– показателями умеренной тесноты связи, а - значения 0,79 и более – показателями высокой тесноты связи.
Посмотрим «ось значимости», зная, что n=10 Рис.5.
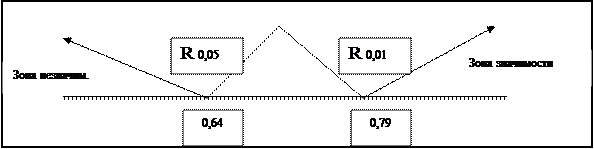
Рис. 5. Ось значимости по критерию Спирмена для выборки n=10.
Критические значения выборочного коэффициента корреляции рангов для 10 испытуемых представлены на Рис.6.
| N | p | |
| 0.05 | 0.01 | |
| 0.64 | 0.79 |
Рис.6. Критические значения выборочного коэффициента корреляции рангов.
Нами исследовалась корреляционная связь между шкалами теста Холла и показателем по шкале поддержки по методике «САТ». Подробные расчеты приведены в Таблицах 3 и 4:
Таблица 3
Результаты статистической обработки ранговых корреляций между шкалой поддержки САТ и шкалой интегративного уровня по тесту Холла
| № | Aсат | Rсат | Вхолл | Rхолл | d | d² |
| 0 | ||||||
| 0 | ||||||
| 7,5 | -0,5 | 0,25 | ||||
| -2 | 4 | |||||
| 1 | ||||||
| 0 | ||||||
| 0 | ||||||
| 4 | ||||||
| 7,5 | -2,5 | 6,25 | ||||
| Сумма | 17,5 |
Подсчет коэффициента ранговых корреляций осуществлялся по формуле (1) с учетом поправок на одинаковые ранги, которые считаем по формулам
Ta =∑(а³- а) / 12 (2)
Тb =∑(b³- b) /12 (3)
Где а – объем каждой группы одинаковых рангов в ранговом ряду Rсат;
b - объем каждой группы одинаковых рангов в ранговом ряду Rхолл
rs = 1- 6*17,5+0,5 / 10*(10²- 1) = 0,8934
Результаты статистической обработки ранговых корреляций между шкалой поддержки САТ и отдельными шкалами по тесту Холла приведены в Таблицах с 4 по 8 в Приложении 3.
Сводные результаты статистической обработки приведены в Таблице 9.
Таблица 9
Сводные результаты статистической обработки корреляционной связи между шкалами эмоционального интеллекта и шкалой поддержки САТ
| Эмоциональная осведомленность | Управление своими эмоциями | Самомотивация | Эмпатия | Распознавание эмоций других людей | Интегративный уровень | |
| Шкала поддержки САТ | 0,94** | 0,86** | 0,79* | 0,74* | 0,55 | 0,89** |
** - р≤ 0,01
* - р≤ 0,05
