На практиці часто результати прямих вимірювань бувають взаємозалежними. Це звичайно буває місце при вимірюванні двох і більш однорідних величин. Наприклад, смугу пропускання знаходять як різницю двох частот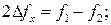 
ємність визначають методом зміщення з виразу 
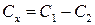тощо.
Відліки цих однорідних величин лежать, як правило, на близькій відстані один від одного по шкалі. Відліки при таких вимірюваннях роблять один за іншим через невеликі проміжки часу. Тому варто очікувати, що вплив деяких факторів, наприклад зовнішньої температури, нестабільності джерел живлення та ін., що впливають на похибку, буде майже однаковим. При розрахунку різниці результатів прямих вимірювань частина похибок (випадкових і систематичних), обумовлені цими факторами, компенсується. Залишаться в основному похибки, обумовлені тими факторами, що встигли між замірюваннями змінитися. Цей зв’язок не функціональний, тому що при багаторазових вимірюваннях похибки будуть різними. Отже, буде мати місце імовірнісний зв’язок між похибками, тобто вони будуть корельовані. Коефіцієнт кореляції може приймати значення 
, і для розрахунку похибки варто користуватися формулою(2.5) чи (2.6), а для розрахунку коефіцієнта кореляції – формулою (2.4). Слід зазначити, що ці формули справедливі для великих 
. При замінюванні істинного значення величин 
і 
на їх середнє арифметичне й при великих формула (2.4) вимагає корекції. Корекція її здійснюється таким же самим чином, як і формула дисперсії при прямих вимірюваннях.
З урахуванням цього формула для розраховування коефіцієнта кореляції буде
(2.9)
або
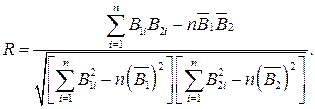
Формула для розраховування загальної середньоквадратичної похибки буде
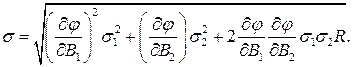
Якщо функціональна залежність між результатами прямих вимірювань має формулу, зручну для логарифмування, і у формулу входять різнорідні фізичні величини, наприклад 
, то зручно користуватися відносними середньоквадратичними похибками. У цьому випадку, відносна середньоквадратична похибка результату непрямого вимірювання буде визначатися за формулою
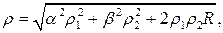
де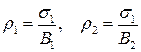 
– відносні середньоквадратичні похибки прямих вимірювань.
На практиці часто роблять вимірювання двох однорідних величин, а потім обчислюють їхню різницю. Наприклад, при методі зміщення, при вимірюванні смуги пропускання тощо. У цьому випадку
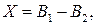
і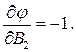 
Отже,
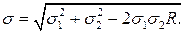
Таким чином, ми завершили розгляд найбільше розповсюджених випадків опрацювання результатів непрямих вимірювань.
Література
1. Бурдун Г.Д., Марков Б.Н. Основы метрологии. – М.: Изд Стандартов, 1975, 335с.
2. Грановский В.А., Сирая Т.Н. Методы обработки экспериментальных данных при измерениях. – Л.: Энергоатомиздат, 1990, 228с.
3. Поліщук Є.С., Дорожовець М.М., Яцук В.О. Метрологія та вимірювальна техніка. Львів: Бескід Біт, 2003, 544с.
