Результат непрямих вимірювань визначається шляхом розрахунку за якою небудь формулою. Величини, що підставляються у формулу, виходять із прямих вимірювань. Ці величини містять відомі похибки. Отже, і отриманий результат буде містити помилку. Це положення справедливе й для випадкових, і для систематичних похибок.
Варто врахувати, що при непрямих вимірюваннях у кінцеву формулу можуть входити:
а) наближені величини, що є ірраціональними числами. Наприклад, 
тощо. Ці величини можуть бути взяті з будь-яким ступенем точності, і тому їх можна вважати постійними;
б) наближені значення різних фізичних сталих. Наприклад, 
- швидкість світла; 
- постійна Больцмана; 
- заряд і маса електрона тощо. Ці величини отримані в результаті численних і складних вимірювань і мають більш високий ступінь точності в порівнянні з точністю звичайних вимірювань. Тому ці фізичні величини можна вважати практично точними;
в) наближені значення фізичних величин, отримані в результаті прямих вимірювань. Ці значення й містять як систематичні, так і випадкові похибки.
Розгляньмо методику визначення випадкових похибок при непрямих вимірюваннях. Будемо вважати, що систематичні похибки величин, отримані в результаті прямих вимірювань, виключені.
Нехай шукана величина 
залежить від двох вхідних у її розрахункову формулу величин 
і 
, тобто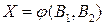 
.Величини й отримані в результаті багаторазових вимірювань, і їх середні арифметичні значення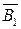 
і 
, а також їхні похибки відомі.
Якщо і одержали приріст 
і 
, то величина одержить приріст 
:
.
Розкладімо праву частину цієї рівності в ряд Тейлора
Виконуючи лінійну інтерполяцію (зневажаючи похідними вище першої), одержимо
. (2.1)
Слід зазначити, що в деяких випадках функціональна залежність між 
і може бути така, що частинна похідна при визначених значеннях аргументу дорівнює нескінченності. Наприклад:
Отже в околі цих крапок користуватися формулою (2.1) не можна. У цьому випадку необхідно робити параболічну апроксимацію, тобто враховувати і другі похідні.
Визначімо похибку результату непрямого вимірювання для випадку лінійної апроксимації. Для цього зробімо 
вимірювань величин і .
Похибка для 
-го вимірювання буде дорівнювати
Піднесімо цей вираз у квадрат:
Просумуймо цю рівність по усім :
Розділивши праву і ліву частини на , одержуємо:
З огляду на що:
тоді
(2.2)
Розгляньмо співмножник 
останнього доданка, виразивши збільшення через залишкові похибки,
(2.3)
З теорії ймовірності відомо, що коефіцієнт кореляції
При великих математичне сподівання буде:
З урахуванням цих виразів коефіцієнт кореляції можна записати у вигляді:
при 
,
а з урахуванням (2.3)
(2.4)
З (2.4) випливає, що
Тоді (2.2) запишімо як
(2.5)
У загальному випадку
(2.6)
Тут
- коефіцієнт кореляції величин 
і 
;
Знак 
у формулі (2.6) визначає, що підсумовування поширюється на всі різні парні комбінації величин 
. За цією формулою розраховують середньоквадратичну похибку результату непрямого вимірювання згідно з відомою функціональною залежністю й відомими середньоквадратичними похибками прямих вимірювань.
Варто розрізняти два випадки. Перший випадок, коли і незалежні, другий випадок, коли і залежні.
