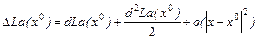Введение.
Мы будем рассматривать функции 
, где 
будет меняться по некоторой области пространства 
. Основным понятием, которое мы использовали для получения результатов для функций одной переменной, было понятие предела функции в точке и всё, с ним связанное. При доказательствах теорем о пределах использовались свойства модуля действительных чисел, а именно следующие: (1) 
;
(2) 
; (3) 
. Сейчас мы введём понятие, аналогичное понятию модуля, для точек из . Это можно сделать разными способами. Приведём три из них, хотя существуют и другие.
1(Евклидова метрика).
Положим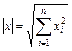 
.Легко проверить первые два свойства, проверим третье (неравенство треугольника). Нужно доказать, что
.
Возведя в квадрат, получим 
.
Это неравенство верно, если левая часть отрицательна или равна нулю. Если она положительна, рассмотрим квадратный трёхчлен
. В силу последнего неравенства, его дискриминант неположителен,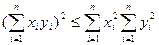 
,что и требовалось доказать.
2(Кубическая метрика).
Положим 
. Все свойства легко проверяются.
3(Октаэдрическая метрика). Положим 
. Опять все свойства проверяются легко.
Любая из этих метрик позволяет определить понятие предела, сходимости, непрерывности, окрестности, предельной точки. В дальнейшем, в зависимости от рассматриваемых задач, будут использоваться первые две метрики. С точки зрения сходимости и непрерывности они приводят к одинаковым результатам, поскольку в любой окрестности с точки зрения метрики 1 содержится окрестность с точки зрения метрики 2 и наоборот.
Операция 
называется введением нормы, если она удовлетворяет требованиям(1)-(3).
Расстояние с помощью нормы определяется как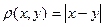 
(это, собственно, и есть метрика!). Проверяется, что обычные свойства расстояния на плоскости выполняются (проверяются так же, как для нормы).
1. Некоторые подмножества в
окрестностью точки 
называется множество точек 
, для которых 
.Обозначение – старое: 
.
Было бы полезно для читающего построить окрестности какой-нибудь точки плоскости в трёх приведённых метриках.
Определение 1.1. Множество 
называется открытым, если любая его точка принадлежит ему вместе с некоторой своей окрестностью.
Определение 1.2. Точка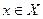 
называется предельной точкой этого множества, если в любой окрестности точки содержится бесконечномного точек множества 
.
Определение 1.3. Множество называется замкнутым, если оно содержит все свои предельные точки.
Множества 
одновременно замкнуты и открыты.
Определение 1.4. Множество 
называется дополнением множества .
Очевидно,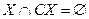 
.
Теорема 1.1 (о дополнении). Дополнение к открытому множеству замкнуто, дополнение к замкнутому – открыто.
Доказательство. 1.Пусть - открытое множество. Нужно доказать, что 
замкнутое. Пусть 
- предельная точка множества 
. Тогда в любой окрестности точки есть элементы множества .Следовательно, не может принадлежать , которое состоит из точек, входящих в него вместе с некоторой окрестностью. Значит,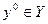 
.
2.Пусть - замкнутое множество. Нужно доказать, что открыто. Если это не так, найдётся точка 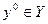, в любой окрестности которой есть элементы из . Но тогда она – предельная для , и, следовательно, должна принадлежать .Противоречие. Теорема доказана.
Теорема 1.2 (о замкнутости и открытости пересечений и объединений множеств). Имеют место следующие утверждения:1)Объединение любого количества (конечного или бесконечного) открытых множеств открыто;2)Объединение конечного числа замкнутых множеств замкнуто;3)Пересечение любого числа замкнутых множеств замкнуто;4)Пересечение конечного числа открытых множеств открыто.
Доказательство. 1) Любая точка объединения принадлежит хотя бы одному из множеств объединения, в которое (они все – открытые!) она входит вместе с некоторой окрестностью; но тогда эта окрестность содержится и в объединении.2) Пусть 
- сходящаяся последовательность из конечного объединения замкнутых множеств. Тогда у неё есть подпоследовательность, целиком состоящая из элементов одного из этих множеств. Поскольку подпоследовательность сходится к той же точке, а множество замкнуто, должна принадлежать тому же множеству; но тогда она принадлежит и объединению. 3) Предельная точка пересечения замкнутых множеств является предельной для любого из них и, следовательно, принадлежит всем им, т.е., пересечению. 4) Следует из того, что пересечение окрестностей – окрестность. Теорема доказана.
Задача: показать, что если в 2) и 4) отбросить требование конечности числа множеств, утверждения станут неверными.
Теорема 1.3(для особо любопытных) 
.
Определение 1.5. Непрерывной кривой, соединяющей точки 
, называется векторная функция 
, где 
, 
и 
.
Вместо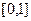 
может быть любой отрезок. Определение означает, что при переходе от одной точки к другой координаты меняются непрерывно.
Определение 1.6. Множество называется связным, если любые две его точки можно соединить непрерывной кривой, состоящей из точек множества .
Определение 1.7. Множество называется ограниченным, если его можно поместить в некоторую окрестность одной из его точек(можно определять это понятие и иначе).
Определение 1.8. (Полярные координаты) На плоскости можно ввести систему координат следующим способом. Выберем какую-нибудь точку, 
, и произвольную полупрямую с началом в этой точке (полярную ось). На полупрямой выберем единичный отрезок. Тогда любой точке плоскости можно сопоставить две координаты: расстояние от до этой точки, 
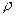, и угол 
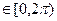отсчитываемый против часовой стрелки от полупрямой до направления на выбранную точку. Если на той же плоскости введены декартовы координаты, начало которых совпадает с точкой , а ось Ох совпадает с полярной осью и единичные отрезки одинаковы, то имеем: 
, и 
. Аналогичную конструкцию можно соорудить для пространства большего числа измерений, но пока она нам не понадобится.
2. Пределы и непрерывность функций
2.1.Определение предела функции ничем не отличается внешне от определения предела для функций одной переменной:
, или аналогичное определение в окрестностях. Поэтому все утверждения, доказанные с использованием свойств модуля, остаются верными и для функций нескольких переменных. Точно так же, остаётся верным утверждение о том, что определение предела по Коши эквивалентно определению предела по Гейне.
Геометрически предел функции при 
означает, что вся окрестность точки стягивается к этой точке. На плоскости можно ввести полярные координаты, для которых начальной точкой будет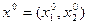 
; тогда, если полярная ось параллельна оси Ох, а угол отсчитывается от неё до направления на точку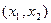 
, будем иметь 
, где 
; предел функции с точки зрения координат 
- это предел при 
и , меняющемся произвольно.
Примечание. Есть разница между 
и 
; второй из этих пределов называется повторным; в нём сначала берётся внутренний предел от функции одной переменной 
, а потом – внешний предел по переменной 
.Может существовать 
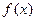, а оба повторных(или один из них) не существовать, могут существовать оба повторных, но не существовать общий предел.
Примеры:1. 
; 2. 
при 
.
2.2.Определение непрерывной функции ничем не отличается от аналогичного определения для функций одной переменной. Доказательства свойств остаются точно такими же. Пример функции 
показывает, что функция, непрерывная в точке по каждой из переменных, может не быть непрерывной как функция двух (или большего числа) переменных.
2.3.Теоремы Коши, Вейерштрасса и Кантора.
Теоремы Вейерштрасса, объединённые в одну, для функций многих переменных выглядят так.
Теорема Вейерштрасса. Пусть функция 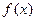непрерывна на замкнутом ограниченном множестве. Тогда она достигает на этом множестве своих максимума и минимума.
Доказательство может быть получено точно таким же способом, как для одномерного случая (от противного, с использованием аналога леммы о стягивающихся отрезках (леммы о стягивающихся кубах), либо самой этой леммы с помощью проекции на оси координат).
Теорема Коши. Пусть функция 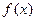непрерывна на связном множестве , пусть 
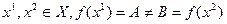. Тогда 
, такой, что 
.
Доказательство получается почти автоматически, если соединить точки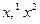 
непрерывной кривой. Вдоль этой кривой функция 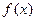будет непрерывной функцией одной переменной, для которой теорема Коши уже доказана.
Теорема Кантора. Функция, непрерывная на ограниченном замкнутом множестве, равномерно непрерывна на нём.
Доказательство – такое же, как для функций одной переменной.
3.Дифференцируемость функций нескольких переменных.
Определение 3.1. Функция 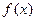называется дифференцируемой в точке , если она определена в некоторой окрестности этой точки, , и её приращение в этой точке может быть представлено в виде
, где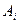 
- константы, зависящие только от точки , а 
.
Следствие 3.1. Функция, дифференцируемая в точке, непрерывна в этой точке.
3.2.Частные производные.(Определение 3.2)
Пусть все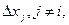 
равны 0. Тогда функция 
, и
, где 
- бесконечномалая при 
. Иными словами, 
, и 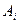- её производная в точке 
. Эта производная называется частной производной функции 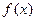в точке по переменной 
.
Следствие 3.2. Если функция дифференцируема в точке, то все её частные производные в этой точке существуют.
Определение 3.3. Выражение
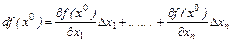для дифференцируемой функции называется дифференциалом этой функцией в точке или главной (линейной) частью её приращения в этой точке. Вектор 
называется градиентом функции в точке .
Следствие 3.3.(Необходимое условие локального экстремума) В точке локального экстремума дифференцируемой функции градиент равен нуль-вектору.
Доказательство. Если зафиксировать все координаты, кроме одной, то получится функция одной переменной. Если исходная функция нескольких переменных имеет в точке локальный экстремум, то наша функция одной переменной имеет там локальный экстремум, значит, её производная там должна равняться 0.
Как показывает пример функции 
, наличие частных производных не является гарантией даже непрерывности. Далее будет приведено достаточное условие дифференцируемости, но сначала разберёмся с разностью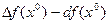 
. Положим 
. Тогда 
для дифференцируемой функции и обратно (т.е., эти записи остаточного члена эквивалентны). В одну сторону доказательство очевидно: 
, и сумма является бесконечномалой при , так как все дроби не превосходят 1. С другой стороны, если разность между приращением и дифференциалом может быть представлена в виде 
, то 
.
Очевидно, что выражения в скобках стремятся к 0 при .
Теорема 3.3.1. Если частные производные функции 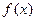в точке непрерывны, то функция в этой точке дифференцируема.
Доказательство. Предположим, что условия теоремы выполнены. Имеем
Теорема доказана.
Можно несколько ослабить условия, потребовав непрерывности всех частных производных, кроме одной. Но вообще условия теоремы не являются необходимыми.
Функция может быть дифференцируемой в точке, не будучи непрерывной ни в какой её окрестности, например 
, где 
- функция Дирихле от 
.
3.4. Производная вдоль вектора или по направлению
Определение 3.4.1. Пусть функция 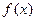определена в некоторой окрестности 
точки и пусть 
- некоторый вектор. Производной вдоль вектора 
функции 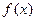и точке называется, если он существует, предел
; если вектор - единичный, получившаяся производная называется производной по направлению.
Теорема 3.4.1. Если функция дифференцируема в точке , то 
.
Доказательство. Запишем приращение вдоль вектора
Поделив на 
и взяв предел при 
получим доказательство, т.к. все 
.
3.5.Геометрический смысл дифференцируемости
Как и для случая одной переменной, дифференцируемость функции в точке эквивалентна наличию касательной плоскости (невертикальной) к графику функции в этой точке.
Определение касательной плоскости к графику функции аналогично случаю функции одной переменной.
3.6.Замена переменных и инвариантность формы первого дифференциала
Пусть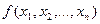 
определена в некоторой окрестности точки 
, и пусть 
. Функции 
предполагаются дифференцируемыми. Мы докажем, что при этих условиях функция 
будет дифференцируема в точке 
и получим формулы для вычисления её частных производных.
Имеем
При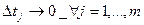 
обе суммы слева будут 
, так как 
.
Следовательно, 
и форма дифференциала не зависит от того, будут независимыми 
или нет. Мы доказали инвариантность формы первого дифференциала.
Имеем, далее
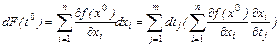. Выражение при 
- это производная 
.
Понятно, что инвариантности второго дифференциала и старших дифференциалов не будет (её нет для частного случая – функций одной переменной). Но сначала их надо определить.
3.7. Дифференциалы старших порядков.
3.7.1. Будем считать, что - независимые переменные. Частные производные могут быть дифференцируемыми функциями от 
, и в этом случае можно определить второй дифференциал 
. Вообще, если 
уже определён и является дифференцируемой функцией, то 
.Для наших целей в основном требуется второй дифференциал.
Если вычислять его непосредственно, получится примерно вот что (ограничимся случаем двух переменных, чтобы формулы выглядели проще).
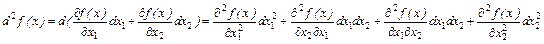
Два средних члена этой суммы называются смешанными производными. Пример функции
показывает, что они могут быть различными. Однако для «хороших» функций значение смешанных производных не зависит от порядка дифференцирования.
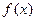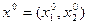Теорема 3.7.1. Пусть функция определена в некоторой окрестности точки и 
. Пусть смешанные вторые частные производные, 
существуют и непрерывны в той же окрестности. Тогда 
.
Доказательство. Рассмотрим дробь
, где 
выбраны так, чтобы точки оставались внутри . Пусть 
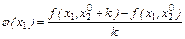. Тогда
.Функция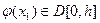 
, по теореме Лагранжа получим 
.
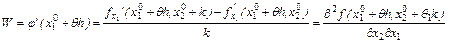Преобразуя 
другим способом, получим
.Устремляя к 0 и пользуясь непрерывностью вторых смешанных производных, получим нужное равенство. Теорема доказана.
Другой вариант условий, при которых смешанные производные не зависят от порядка дифференцирования, - потребовать, чтобы 
. По индукции можно доказать следующий результат: значение смешанных производных любого порядка не зависит от порядка дифференцирования, если эти производные непрерывны в исследуемой точке.
3.7.2. Рассмотрим теперь случай когда 
.
Имеем
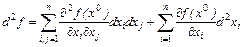. Есть один случай, когда вторая сумма равна нулю: так будет, если для всех 
, т.е. если замена линейная. Если она имеет вид 
, старшие дифференциалы заведомо будут инвариантны при такой замене.
4.Формула Тэйлора
Теорема 4.1. Пусть функция 
. Тогда
Доказательство. Пусть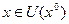 
. Тогда точку отрезка 
можно записать в виде
. На указанном отрезке 
будет функцией одной переменной, . Для функции
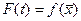имеет место формула Тэйлора
, где 
. Далее,
так как 
- константа. Аналогично, 
, 
.Вспомним теперь, что нас интересует 
. В этом случае 
, и теорема доказана.
5. Достаточное условие локального безусловного экстремума
Теорема 5.1. Пусть 
и - точка, в которой выполнено необходимое условие локального экстремума. Тогда, если 
, в точке минимум, если 
, в точке максимум, если второй дифференциал меняет знак, то в точке нет экстремума; если второй дифференциал полуопределён, требуется дополнительное исследование.
Доказательство. Формула Тэйлора в стационарной точке выглядит так
Доказательство. Разберём один случай, так как все они исследуются одинаково, кроме последнего, в котором существенно поведение 
. Пусть
, где коэффициенты – вторые производные в точке .
Сумма, на которую умножается 
, определена на единичной сфере и по теореме Вейерштрасса достигает там максимума и минимума. Если она положительно определена, то минимум 
не может быть отрицательным или равным нулю. В этом случае поведение несущественно. Тот же вывод имеет место, если она отрицательно определена или меняет знак.
Если же квадратичная форма полуопределена, то можно привести разнообразные примеры (как в случае функций одной переменной при равном нулю втором дифференциале). Теорема доказана.
Теорема о неявной функции
Теорема о неявной функции является одной из важнейших теорем математического анализа. Она рассматривает задачу о разрешимости уравнения f(x,y)=0 относительно y; в разных её вариантах x,f,y могут быть скалярами или векторами. Следствия из неё широко используются, в частности, в теории условного экстремума и в экономических приложениях. Далее эта теорема, вместе с некоторыми приложениями, будет изложена в различных вариантах.
1.Рассмотрим функцию u = f (x,y), имеющую непрерывные частные производные в некоторой окрестности U(a,b) точки (a,b).
Теорема 1. Пусть производная по y функции f (x,y) в точке (a,b) отлична от 0, f(a,b)=0.
Тогда найдётся окрестность U0(a,b), в которой y можно представить как функцию от x, y=w(x), такую, что b=w(a), w является дифференцируемой функцией от x, и w ′= - f ′x/f ′y.
Доказательство. Для определённости, пусть производная по y в точке a положительна. Тогда функция f(a,y) монотонно возрастает в точке b и, значит, для y>b f (a,y)>0, а для y<b f(a,y)<0. Рассмотрим теперь две функции, f(x,b-e) и f(x,b+e), выбрав e так, чтобы мы не вышли за U(a,b). Поскольку f(x,y) имеет непрерывные частные производные в U(a,b), она там дифференцируема и, значит, непрерывна; следовательно, функции f(x,b-e), f(x,b+e) непрерывны в некоторой общей для них окрестности точки a, (a-s,a+s). Согласно лемме об устойчивости знака, s можно выбрать так, чтобы во всей этой окрестности выполнялись неравенства f(x,b-e)<0, f(b+e)>0.
Рассмотрим теперь окрестность (a - s,a + s). Для всякого x из этой окрестности функция F(y)=f(x,y) монотонно возрастает как функция от y и непрерывна; по теореме Коши о промежуточном значении, найдётся точка y из (b-e,b+e), в которой F(y)=0, и в силу монотонности F такая точка только одна. Мы доказали, что в окрестности V(a,b) для всякого x из (a-s,a+s) найдётся единственный y из (b-e,b+e), для которого f(x,y)=0. Положим y=w(x). Тогда f(x,w(x))=0 по определению w(x) для всех x из (a-s,a+s).
Докажем теперь, что w(x) непрерывна в (a-s,a+s). Для точки a непрерывность очевидна: мы по e выбрали s, такое, что как только x попадает в s-окрестность точки a, y попадает в е - окрестность точки b, Если взять любую другую точку (x1,y1), x1 из (a‑s,a+s), y1 из (b-e,b+e), такую, что f(x1,y1)=0, то для неё будут выполнены те же условия, что для (a,b). Значит, у неё найдётся окрестность, в которой y=w1(x) и w1 непрерывна в x1. Но w1(x)=w(x), так как условие f(x,w(x))=0 однозначно определяет функцию w(x).Следовательно, y=w(x) непрерывна для всех x из (a-s,a+s).
Докажем, что w(x) дифференцируема.
Как было отмечено выше, f(x,y) дифференцируема в U(a,b). Рассмотрим приращение f(x,w(x))-f(a,b)=0=f 
(a,b)*(x-a)+f′y(a,b)*(w(x)-b) + 
*(x – a) + 
*(w(x) –b), где и бесконечно-малые. Выберем такую окрестность точки (a,b) чтобы f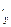 
+ 
0. Это можно сделать, потому что бесконечно малая. Эта окрестность и есть U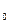 
(a,b). Имеем
= 
При x стремящемся к a w(x) стремится к b, и - к 0. Получаем
w 
= - 
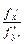
Если рассмотреть другую точку из U 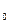(a,b), то, рассуждая как при доказательстве непрерывности w(x), получим, что w(x) дифференцируема для всех (x,w(x)) из U 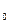(a,b).
Теорема доказана.
Примечания. 1. Для доказательства существования w(x) достаточно потребовать непрерывность f(x,y) и её монотонность по y.
2.Требование неравенства 0 производной по y (или по x) не является необходимым. Уравнение (y-x) 
=0 однозначно разрешимо, хотя обе частные производные равны 0.
2. Теорема 2. Пусть функция u=f(x1,x2,…..,xn,y) =f(x,y) определена и непрерывна вместе со своими частными производными в некоторой окрестности 
точки 
, причём 
, и имеет ненулевую частную производную по y в самой точке . Тогда существует окрестность 
, в которой y=w(x)=w(x1,x2,…..,xn), функция w(x) непрерывна вместе со своими частными производными в окрестности , 
и
= - 
Доказательство этой теоремы совершенно аналогично доказательству Теоремы 1.
Следствие 1. (Уравнение касательной к неявной функции) Пусть выполнены условия Теоремы 2. Тогда уравнение касательной к функции y=w(x) в точке может быть записано в виде
Действительно, уравнение касательной к y=w(x) в указанной точке имеет вид
Умножив его на 
и перенеся всё в левую часть, получим, что требовалось доказать.
Легко получить тот же результат из геометрических соображений. Действительно, если уравнение касательной к графику функции u=f(x,y) в точке имеет вид
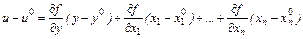
то при сечении графика плоскостью u=u 
из графика высекается множество уровня, а из касательной плоскости к графику – касательная к множеству уровня.
Следствие 2. Пусть в условиях Теоремы 2 рассматривается уравнение f(x,y)=c,где c – некоторая константа, и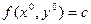 
. Рассмотрев функцию u 
=f(x,y)-c, мы увидим, что она удовлетворяет условиям Теоремы 2. По Следствию 1, получим касательную к соответствующей неявной функции в виде
С другой стороны, уравнение f(x,y)=c представляет множество уровня функции f. Теорема 2 показывает, что множество уровня является некоторой поверхностью, касательная к неявной функции w(x) в точке – касательной к этой поверхности, а уравнение касательной, которое мы получили, - что градиент функции f в точке ортогонален поверхности уровня функции f
Формулировка Следствия 2. Пусть функция u=f(x,y) определена в некоторой окрестности точки , пусть её частные производные непрерывны в этой точке, производная по y в этой точке отлична от нуля и 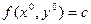. Тогда в некоторой окрестности точки множество уровня f=c является поверхностью, и градиент функции f ортогонален этой поверхности уровня в точке .
3. Теорема 3 (о векторной неявной функции). Пусть функции f1(x1,x2,….,xn,xn+1,…xn+m), …..,fm(x1,x2,….,xn,xn+1,…xn+m) непрерывно дифференцируемы в некоторой окрестности точки , пусть
,
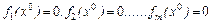и пусть определитель 
,
отличен от нуля. Тогда найдётся окрестность 
точки , в которой
xn+1=w1(x1,x2,….,xn),…,xn+m= wm(x1,x2,….,xn), причём функции w1,…,wm
непрерывно дифференцируемы и
f1(x1,…,xn,w1,…,wm)=0,…,fm(x1,…,xn,w1,…,wm)=0.
Теорема утверждает, что, если выполнены её условия, последние координаты точки 
в некоторой окрестности точки 
можно выразить как непрерывно-дифференцируемые функции первых.
Доказательство (индукция по числу уравнений).
Если m=1, то мы находимся в условиях Теоремы 2, и всё доказано.
Пусть m>1. Предположим, что теорема уже доказана для всех k<m, в частности, для k=m-1. Рассмотрим последнее уравнение. Поскольку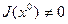 
, и поскольку частные производные, из которых он составлен, непрерывны, по лемме об устойчивости знака найдётся окрестность точки , 
, в которой он будет всё ещё отличным от нуля. В этой окрестности хотя бы один из элементов его последней строки будет отличен от нуля. Пусть, для определённости, это будет её последний элемент, 
. Тогда, по Теореме 2, найдётся окрестность 
, в которой xn+m можно будет выразить в виде функции w0(x1,…,xn+m-1). В окрестности система уравнений, данная в условиях Теоремы 3, будет эквивалентна системе
……………………
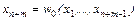
Рассмотрим теперь систему из последних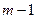 
уравнений. Если мы докажем, что в некоторой окрестности точки x0 определитель
не равен нулю, то, используя предположение индукции, мы выразим xn+1,…,xn+m-1 как функции от x1,…,xn, которые будут непрерывно-дифференцируемыми. Подставив эти функции в w0, получим выражение для xn+m в виде непрерывно-дифференцируемой функции от x1,…,xn, и Теорема 3 будет доказана.
Докажем, что 
отличен от нуля. Для этого в определителе J к 
тому,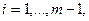 
столбцу прибавим последний, умноженный на 
; получим 
Определитель размерности (m-1), стоящий в левом верхнем углу, есть просто В нижней строке
Получаем 
Значит, 
, и Теорема 3 доказана.
Примечания. 1. Теорема 3 не утверждает, что, при отличном от нуля якобиане на всей области определения функций f1,…,fm, последние координаты однозначно во всей области определяются по первым. Для системы 
якобиан всюду отличен от нуля при >0 (он равен x), но однозначной разрешимости относительно u и v не будет.
2.Легко сообразить, что Теорема 3 утверждает следующее. Если градиенты функций f1,…,fm линейно-независимы в точке , то в некоторой окрестности точки m её координат можно рассматривать как функции от остальных.
Теория локального условного экстремума
В этом разделе будет рассматриваться следующая задача:
Найти экстремумы функции u=f(x)=f(x1,…,xn) при условиях f1(x)=0,….,fm(x)=0, m<n; все функции предполагаются непрерывными вместе с первыми или, по потребности, со вторыми частными производными, а градиенты функций f1,….,fm – линейно-независимыми. Мы будем, кроме того, предполагать, что все рассматриваемые точки содержатся в области определения функции f(x) вместе с некоторой окрестностью (открытой) и что пересечение этой окрестности с множеством точек, удовлетворяющих условиям f1(x)=0,…,fm(x)=0 не пусто. Сами условия обычно называются уравнениями связей.
Точка удовлетворяющая уравнениям связей, называется точкой локального условного экстремума функции f(x), если значение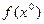 
является самым большим или самым маленьким среди значений f(x) для точек x, удовлетворяющих уравнениям связей (соответственно, получается локальный условный максимум или локальный условный минимум).
Необходимое условие локального условного экстремума.
1). Разберёмся сначала с геометрией. Пусть удовлетворяет системе уравнений f1=0,…,fm=0. Множество векторов 
, касательных в точке к гладкой поверхности 
, которую, согласно Теореме 3, порождают точки, удовлетворяющие этой системе, является множеством решений системы
,
где 
- градиенты к поверхностям, высекаемым из общей области допустимых x-ов отдельными ограничениями. Это множество называется касательным многообразием 
в точке к поверхности . Если градиент функции f в точке имеет ненулевую проекцию на , то на есть направление, в котором функция f возрастает, и, значит, на есть точки x, в которых значение f(x)>f(x0), и, точно так же, есть точки x, в которых значение f(x)<f(x0). В этом случае точка не может быть точкой локального условного экстремума. Значит, необходимым условием того, чтобы точка была точкой локального условного экстремума, является равенство нулю проекции градиента на , что означает, что сам градиент функции f в точке лежит в ортогональном дополнении к . В свою очередь, ортогональное дополнение к порождается градиентами ограничений, взятыми в точке , которые у нас, по условию, линейно-независимы. Мы получили следующее необходимое условие: точка может быть точкой локального условного экстремума функции f при условиях f1=0,…,fm=0 только в том случае, если градиент функции f в точке есть линейная комбинация градиентов ограничений, то есть
…..+ 
* 
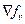2). То же самое условие можно получить иначе. Рассмотрим функцию
La(x1,x2,…,xn;y1,…,ym) = f +(y1)*f1 + (y2)*f2 + …+ (ym)* fm.
Ясно,что при любых y,при условиях
f =0,…., 
экстремумы функций f и La совпадают. Подберём y так, чтобы условный экстремум функции f совпадал с безусловным экстремумом функции La. Приравняем нулю частные производные функции Лагранжа. Получим
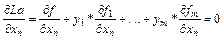
Пусть - точка условного экстремума функции f при заданных условиях. Частные производные функции Лагранжа по переменным y задают ровно эти самые условия. Рассмотрим теперь систему уравнений
в точке . В этой точке определитель, стоящий при переменных y, отличен от нуля по предположению о линейной независимости градиентов ограничений.. Следовательно, можно найти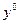 
, являющиеся решением данной системы. Рассматривая далее функцию Лагранжа с коэффициентами 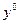, мы видим, что её дифференциал будет равен нулю в том, и только в том случае, если будет выполняться система уравнений
так как 
независимы. Следовательно, с одной стороны, мы получаем, что градиент функции f является линейной комбинацией градиентов ограничений,а с другой стороны, что точки локального условного экстремума
функции f можно искать как точки обычного локального экстремума функции Лагранжа, что и требовалось.
Теорема 4. Для того, чтобы точка была точкой локального условного экстремума, необходимо, чтобы градиент целевой функции был линейной комбинацией градиентов ограничений.
Достаточные условия локального условного экстремума.
Пусть – точка, подозреваемая на условный локальный экстремум, 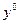– соответствующие множители Лагранжа. Как уже отмечалось, при условиях
экстремумы функций f и La совпадают, равно как и значения в точках, удовлетворяющих условиям. Значит, исследование на наличие экстремума можно проводить с помощью функции Лагранжа. Рассмотрим приращение функции Лагранжа в точке
