Положим  .Тогда определение дифференцируемости в точке
.Тогда определение дифференцируемости в точке 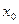 можно записать в виде
можно записать в виде  .Видно, что функция
.Видно, что функция  , дифференцируемая в точке
, дифференцируемая в точке 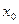 , непрерывна в этой точке, поскольку при
, непрерывна в этой точке, поскольку при  имеем
имеем  . Поделим наше равенство на
. Поделим наше равенство на 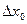 . Получим
. Получим

Следовательно,  Этот предел называется производной функции
Этот предел называется производной функции  в точке
в точке 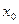 и обозначается одним из следующих символов:
и обозначается одним из следующих символов:  или
или  .Верно и обратное: если у функции
.Верно и обратное: если у функции  в точке
в точке 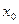 существует производная, то функция в этой точке дифференцируема. Действительно, если производная существует, то
существует производная, то функция в этой точке дифференцируема. Действительно, если производная существует, то  , где
, где  - б.м. при
- б.м. при  . Следовательно,
. Следовательно,  , что и требовалось. Сформулируем доказанное как отдельную теорему.
, что и требовалось. Сформулируем доказанное как отдельную теорему.
Теорема 5.1. Для того, чтобы функция  была дифференцируемой в точке
была дифференцируемой в точке 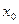 , необходимо и достаточно, чтобы она имела там производную.
, необходимо и достаточно, чтобы она имела там производную.
Определение 5.2. Дифференциалом функции  в точке
в точке 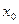 называется произведение
называется произведение  .
.
Если  - независимая переменная, полагают
- независимая переменная, полагают 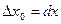 ;
;  не зависит от точки
не зависит от точки 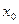 .Дифференциал
.Дифференциал  линейно зависит от
линейно зависит от  . Его называют главной линейной частью приращения функции
. Его называют главной линейной частью приращения функции  в точке
в точке 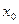 .(Главной, потому что при
.(Главной, потому что при 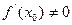 оставшаяся часть приращения функции, равная
оставшаяся часть приращения функции, равная  стремится к 0 быстрее дифференциала).
стремится к 0 быстрее дифференциала).
Теорема 5.2. Пусть  и
и  дифференцируемы в точке
дифференцируемы в точке 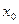 . Тогда
. Тогда

(Последняя формула верна при  ).
).
Доказательство. Докажем последнее утверждение; остальные доказать ещё проще, а схема доказательства сохраняется. Имеем
 .
.
Заметим, что мы имеем право писать  в знаменателе, так как согласно с леммой о сохранении знака
в знаменателе, так как согласно с леммой о сохранении знака 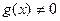 в некоторой окрестности точки
в некоторой окрестности точки 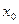 , и можем переходить к пределу в сумме (в числителе) и дроби по свойствам функций, имеющих в
, и можем переходить к пределу в сумме (в числителе) и дроби по свойствам функций, имеющих в 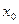 предел.
предел.
Теорема доказана.
Теорема 5.2’. В условиях теоремы 5.2 имеем

Доказательство. Умножим равенства предыдущей теоремы на  .
.
Теорема 5.3(о дифференцируемости сложной функции). Пусть  определена в некоторой окрестности точки
определена в некоторой окрестности точки 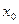 ,
,  , и дифференцируема в самой точке
, и дифференцируема в самой точке 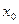 , а функция
, а функция  определена в окрестности
определена в окрестности  точки
точки  , причём (а)
, причём (а)  ,
,  ,и(б) при
,и(б) при  . Тогда сложная функция,
. Тогда сложная функция,  и
и  .
.
Следует заметить, что  и
и  меняются в разных пространствах вещественных чисел!
меняются в разных пространствах вещественных чисел!
Доказательство. Поскольку 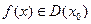 , имеем
, имеем  ,где
,где  - б.м. при
- б.м. при  . Аналогично, поскольку
. Аналогично, поскольку  , имеем
, имеем  , где
, где  - б.м. при
- б.м. при  .Объединяя эти результаты, получим
.Объединяя эти результаты, получим
 При
При  ,так как
,так как 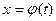
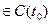 . Значит выражение в скобках при
. Значит выражение в скобках при  является б.м.
является б.м.  Теорема доказана.
Теорема доказана.
Рассмотрим дифференциал функции  в точке
в точке  . По определению, он равен
. По определению, он равен  . Но
. Но  .В этом случае
.В этом случае  , но всё равно имеем
, но всё равно имеем  , т.е. дифференциал функции
, т.е. дифференциал функции  как функции от
как функции от  ищется по той же формуле, что и дифференциал функции
ищется по той же формуле, что и дифференциал функции  как функции от
как функции от  .Это свойство
.Это свойство  называется инвариантностью формы первого дифференциала при замене переменной.
называется инвариантностью формы первого дифференциала при замене переменной.
Теорема 5.3’. Первый дифференциал функции  вычисляется по формуле
вычисляется по формуле 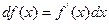 независимо от того, будет
независимо от того, будет  независимой переменной или нет.
независимой переменной или нет.
Это свойство очень важно при при вычислении интегралов. Оно не имеет места для дифференциалов высших порядков в общем случае.
6.Теоремы о дифференцируемых функциях.
Определение 6.1. Функция  называется дифференцируемой на множестве
называется дифференцируемой на множестве  ,если она дифференцируема
,если она дифференцируема  .Это обозначается так:
.Это обозначается так: 
Производная  для
для 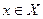 в этом случае является функцией от
в этом случае является функцией от  . Если эта функция является дифференцируемой на
. Если эта функция является дифференцируемой на  , то её производная называется второй производной функции
, то её производная называется второй производной функции  .Обозначение:
.Обозначение:  . Вообще
. Вообще
Определение 6.2. Если  , то, по определению,
, то, по определению,  .Для
.Для  в этом случае пишут
в этом случае пишут  .
.
Определение 6.3. Если  , то
, то  .
.
Рассмотрим теперь вопрос об инвариантности.Если  - независимая переменная, то
- независимая переменная, то  - не зависит от
- не зависит от  , и
, и  (и вообще,
(и вообще,  ).Если
).Если 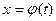 , то
, то  .Значит, если
.Значит, если 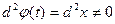 , инвариантности нет.
, инвариантности нет.
Теорема 6.1. Дифференциалы высших порядков не инвариантны, вообще говоря, относительно замены переменной.
Определение 6.4 Пусть функция  определена на интервале
определена на интервале 
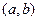 . Точка
. Точка 
 называется точкой локального максимума функции
называется точкой локального максимума функции  , если существует окрестность
, если существует окрестность 
 , для всех точек которой
, для всех точек которой  .Точка
.Точка 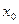 называется точкой строгого локального максимума, если для всех точек окрестности
называется точкой строгого локального максимума, если для всех точек окрестности 
 .
.
Определение 6.5. При тех же условиях на функцию 
 , точка
, точка 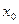 называется точкой локального минимума функции
называется точкой локального минимума функции  , если для всех точек некоторой окрестности выполняется неравенство
, если для всех точек некоторой окрестности выполняется неравенство 
 , и точкой строгого локального минимума, если последнее неравенство – строгое.
, и точкой строгого локального минимума, если последнее неравенство – строгое.
Определение 6.6. Точки локального максимума или минимума называются точками локального экстремума.
Теорема 6.2.(Ферма). Пусть функция 
 определена и дифференцируема на интервале
определена и дифференцируема на интервале 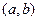 и
и 
 - точка экстремума для
- точка экстремума для 
 . Тогда
. Тогда  = 0.
= 0.
Доказательство.  Предположим для определённости, что
Предположим для определённости, что 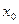 - точка локального максимума. Пусть
- точка локального максимума. Пусть  .Имеем
.Имеем
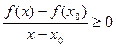 .Значит,
.Значит,  . Пусть теперь
. Пусть теперь  .Рассматривая то же отношение, получим
.Рассматривая то же отношение, получим  .Следовательно,
.Следовательно, 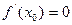 . Теорема доказана.
. Теорема доказана.
Теорема 6.3 (Ролля). Пусть 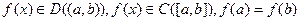 .Существует
.Существует  такая, что
такая, что 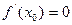 .
.
Доказательство. 1.Если  - константа, то
- константа, то  , и теорема верна. 2.Если функция -не константа, то,во всяком случае, она непрерывна на
, и теорема верна. 2.Если функция -не константа, то,во всяком случае, она непрерывна на  (поскольку дифференцируема).Но тогда она достигает где-то на
(поскольку дифференцируема).Но тогда она достигает где-то на  своего максимума и минимума. Хотя бы одна из этих точек не будет совпадать ни с
своего максимума и минимума. Хотя бы одна из этих точек не будет совпадать ни с  ,ни с
,ни с 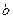 , и потому расположена на
, и потому расположена на 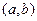 .Значит, она будет точкой локального экстремума, и производная в ней будет равна нулю. Теорема доказана.
.Значит, она будет точкой локального экстремума, и производная в ней будет равна нулю. Теорема доказана.
Теорема 6.4(Коши). Пусть  . Тогда существует точка
. Тогда существует точка  , для которой
, для которой
 .
.
Доказательство. 1.Заметим, что 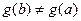 , так как в противном случае по теореме Ролля нашлась бы точка
, так как в противном случае по теореме Ролля нашлась бы точка  , в которой
, в которой  .2. Для функции
.2. Для функции

на  выполнены все условия теоремы Ролля. Найдётся по этой теореме точка
выполнены все условия теоремы Ролля. Найдётся по этой теореме точка  , в которой
, в которой  .Имеем
.Имеем
 ; поделив на
; поделив на  ,получим что требовалось доказать.
,получим что требовалось доказать.
Следствие 6.4.1.(Теорема Лагранжа). Пусть  .Существует
.Существует  , для которой
, для которой
 .
.
Доказательство. Достаточно взять  в предыдущей теореме.
в предыдущей теореме.
Следствие 6.4.2.(«Простое» правило Лопиталя). Пусть функции 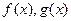 определены в проколотой(и может быть односторонней) окрестности точки
определены в проколотой(и может быть односторонней) окрестности точки 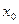 и (1)
и (1)  ;(2)
;(2)  определены в той же окрестности, и (3)
определены в той же окрестности, и (3)  ;(4)пусть существует
;(4)пусть существует  .Тогда
.Тогда  .
.
Доказательство. Пусть 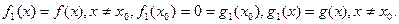
Функции  удовлетворяют условиям теоремы Коши.Значит,
удовлетворяют условиям теоремы Коши.Значит,
 для некоторой точки
для некоторой точки  .При
.При  функции
функции  и
и  совпадают, так что полученное равенство можно переписать как
совпадают, так что полученное равенство можно переписать как
 . При
. При  имеем
имеем 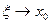 , теорема доказана.
, теорема доказана.
Аналогичная теорема верна для неопределённости  , но её мы доказывать не будем. Желающие могут найти её в 1-ом томе «толстого» Фихтенгольца.
, но её мы доказывать не будем. Желающие могут найти её в 1-ом томе «толстого» Фихтенгольца.
Следствие 6.4.3(Формула Тэйлора с остаточным членом в форме Пеано). Пусть функция  имеет производные всех порядков до (
имеет производные всех порядков до ( )-го включительно в некоторой окрестности
)-го включительно в некоторой окрестности  и производную
и производную  в самой точке
в самой точке 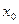 . Тогда для
. Тогда для 

Доказательство. Вычислим предел:
 (Легко видеть, что к данной дроби применимо правило Лопиталя. Применяя его (
(Легко видеть, что к данной дроби применимо правило Лопиталя. Применяя его ( ) раз, получим)
) раз, получим)

(Функция  ,значит
,значит  ,где
,где  - б.м.;)
- б.м.;)
 .
.
Теорема доказана.
Разность 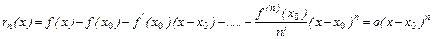
называется остаточным членом формулы Тэйлора в форме Пеано. Ниже, при более жёстких ограничениях на функцию  , мы получим форму остаточного члена, более удобную в приложениях.
, мы получим форму остаточного члена, более удобную в приложениях.
6.5.Остаточный член в форме Шлёмильха – Роша и его варианты.
Пусть функция  определена на отрезке
определена на отрезке  и имеет там непрерывные производные порядков до
и имеет там непрерывные производные порядков до  включительно, и пусть в интервале
включительно, и пусть в интервале  у неё есть конечная
у неё есть конечная  . Пусть
. Пусть  - некоторая точка этого интервала Рассмотрим функцию
- некоторая точка этого интервала Рассмотрим функцию
 ,
,  .
.
Эта функция непрерывна на  и имеет внутри него конечную производную. Кроме того,
и имеет внутри него конечную производную. Кроме того,  .Если вычислить производную в точке
.Если вычислить производную в точке  , получим
, получим
 .
.
Пусть теперь 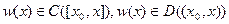 - любая функция, для которой
- любая функция, для которой  при
при  .По теореме Коши, для
.По теореме Коши, для  имеем
имеем
 ,где
,где  или, что то же самое,
или, что то же самое,  ,
,  .Подставляя в эту формулу
.Подставляя в эту формулу  , после умножения на
, после умножения на  , получим
, получим
 .
.
Полагая  , получим
, получим
 .
.
Такая форма остаточного члена называется формой Шлёмильха – Роша.
Если известны какие-нибудь ограничения на модуль производных независимо от их порядка, такая форма позволяет оценивать величину остаточного члена для конкретных 
Особенно употребительны два частных случая. При  получаем остаточный член в форме Лагранжа
получаем остаточный член в форме Лагранжа
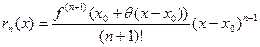 .
.
При  получаем остаточный член в форме Коши
получаем остаточный член в форме Коши
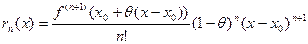 .
.
Полученные формы остаточного члена позволяют более точно оценивать разность  , если известно,например, что модуль производных ограничен какой-либо константой.
, если известно,например, что модуль производных ограничен какой-либо константой.
Теорема 6.6. Если функция  , то обратная функция
, то обратная функция 
Доказательство. При рассмотрении непрерывных функций было доказано, что если на отрезке задана строго монотонная функция, то на области её значений определена однозначно обратная к ней функция, которая будет строго монотонной и непрерывной. Из условий теоремы 6.6 следует, что  строго монотонна. Поэтому существование и непрерывность
строго монотонна. Поэтому существование и непрерывность 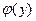 доказывать не нужно. Имеем
доказывать не нужно. Имеем






