Одним из методов выявления взаимосвязей является корреляционно-регрессионный анализ.
Корреляционно–регрессионный анализ включает решение задач двух видов:
- задача корреляционного анализа сводится к измерению тесноты связи между варьирующими признаками;
- задача регрессионного анализа состотт в установлении формы зависимости, определении уравнения регрессии.
Рассмотрим применение приемов корреляционного анализа на конкретном примере (табл. 1).
Таблица 1
Товарооборот и издержки обращения десяти предприятий, млн р.
| Товарооборот | ||||||||||
| Издержки обращения | 0,8 | 1,0 | 0,2 | 0,4 | 0,3 | 0,7 | 0,6 | 0,9 | 0,6 | 0,9 |
При рассмотрении вопросов подбора формы связи особое внимание уделяется глубокому теоретическому анализу изучаемого процесса, установлению причинно–следственных связей. Наиболее распространенным приемом выявления формы связи являются графические изображения.
Графический анализ исходных данных (рис. 1) показывает, что с увеличением товарооборота растут и издержки обращения.
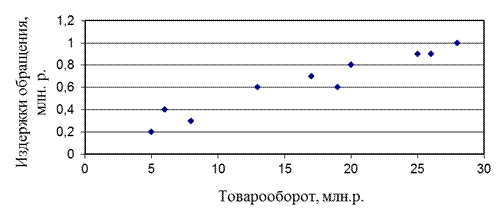
Рис. 1. Зависимость издержек обращения от товарооборота
После того как будет установлено, что зависимость между признаками есть, нужно установить теоретическую форму связи, т. е. вид математической функции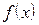 
, которая наилучшим образом описывает поведение изучаемого признака.
Допустим, что между рассматриваемыми показателями существует линейная связь.
Уравнение линейной связи в общем виде можно записать так:
.
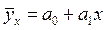Это уравнение, выражающее зависимость y от x, называется уравнением регрессии.
Найти уравнение регрессии означает определить параметры а1 и а0. Их оценивают при помощи метода наименьших квадратов, который дает следующую систему нормальных уравнений:
где х – значения факторного признака, в нашем примере суммы товарооборота (табл. 1, строка 1);
у – значения результативного признака – суммы издержек обращения (табл. 1, строка 2);
n – число парных значений факторного и результативного при–
знаков.
Для составления и решения системы линейных уравнений, т. е. определения параметров, воспользуемся данными табл. 2, в которой рассчитаем необходимые компоненты åх, åу, åх2, åху, исходные данные предварительно ранжируем (располагаем по возрастанию значений факторного признака – товарооборота) и заносим в таблицу 2.
Таблица 2
Расчетная таблица параметров уравнения регрессии
| Номер предприятия | Товарооборот, млн р. (х) | Издержки обращения, млн р. (у) | х2 | ху |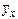 
| у2 |
| А | ||||||
| 0,2 | 1,0 | 0,28 | 0,04 | |||
| А | ||||||
| 0,4 | 2,4 | 0,31 | 0,16 | |||
| 0,3 | 2,4 | 0,37 | 0,09 | |||
| 0,6 | 7,8 | 0,52 | 0,36 | |||
| 0,7 | 11,9 | 0,65 | 0,49 | |||
| 0,6 | 11,4 | 0,71 | 0,36 | |||
| 0,8 | 16,0 | 0,74 | 0,64 | |||
| 0,9 | 22,5 | 0,90 | 0,81 | |||
| 0,9 | 23,4 | 0,93 | 0,81 | |||
| 1,0 | 28,0 | 0,99 | 1,00 | |||
| Итого | 6,4 | 126,8 | 6,40 | 4,76 |
В гр. 3 таблицы 2 вносим квадраты переменных х2 (52, 62, 82 и т.д.), в гр.4 – произведение х на у (5´0,2; 6´0,4; и т.д.).
Итоговые показатели граф (1–4) подставляем в систему нормальных уравнений:
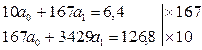
Чтобы уравнять коэффициент при 
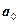каждый член первого уравнения умножаем на 167, второго – на 10 и из второго вычитаем первое:
Параметр а1 =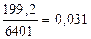 
. Подставим его значение в первое уравнение и найдем параметр аo:
10ао+ 0,031´167 = 6,4,
10ао+ 5,177 = 6,4,
ао =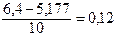 
.
Уравнение регрессии примет вид: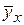 
= 0,12 + 0,031х. Подставляя в него значения х, найдем выравненные, или теоретические значения, 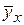. Так, при товарообороте 5 млн р. (х1) теоретическое значение суммы издержек составит: 
= 0,12 + 0,031´5 = 0,28. При товарообороте 6 млн. р.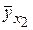 
= 0,12 + 0,031 ´6 = 0,31 и т.д.
Теоретические значения помещены в гр. 5 таблицы 2. Сумма выравненных значений должна быть равна сумме фактических значений результативного признака (
); 6,4 = 6,4. Если такого равенства нет, то следует проверить правильность всех предшествующих расчетов.
Экономический смысл имеет параметр а1, который называется коэффициентом регрессии. Коэффициент регрессии показывает, на сколько единиц в среднем изменится у при увеличении х на единицу. В рассмотренном примере увеличение товарооборота на 1 млн р. ведет в среднем к росту издержек обращения на 0,031 млн р.
В случае установления линейной зависимости между факторным (x) и результативным (y) признаками для оценки тесноты связи между ними рассчитывают линейный коэффициент корреляции:
.
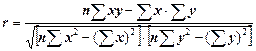Линейный коэффициент корреляции может принимать любые значения от –1 до +1. Чем ближе значение этого коэффициента к 
1, тем более тесная связь предполагается между признаками х и у. Если rху = 0, то это не всегда говорит об отсутствии связи вообще – часто это означает отсутствие линейной связи. В таком случае нужно использовать нелинейные зависимости (уравнение гиперболы, уравнение логарифмической кривой, экспоненциальную зависимость и др.).
Для качественной оценки тесноты связи между признаками используется шкала Чэддока (табл. 3).
Таблица 3
Оценка тесноты связи по шкале Чэддока
| Показатели тесноты связи | 0,1 – 0,3 | 0,3 – 0,5 | 0,5 – 0,7 | 0,7 – 0,9 | 0,9 – 0,99 |
| Характеристика тесноты связи | Слабая | Умеренная | Заметная | Высокая | Очень высокая |
Знак при линейном коэффициенте корреляции указывает направление связи: «+» – прямая связь; «–» – обратная связь.
Рассчитаем линейный коэффициент корреляции для рассмотренного примера, для этого воспользуемся данными итоговой строки таблицы 2:
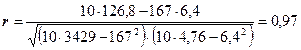
Согласно таблице Чэддока, при r = 0,97 зависимость результативного признака от факторного очень высокая. Следовательно, найденное уравнение регрессии 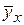= 0,12 + 0,031х можно использовать для прогноза суммы издержек при наличии данных об изменении суммы товарооборота.
