Система индексов в исследовании факторов динамики объемных показателей

ИНДЕКСЫ

План

Индивидуальные и общие индексы. Построение агрегатных индексов.

2. Система индексов в исследовании факторов динамики объемных показателей.

3. Средние индексы из индивидуальных.

 

Индивидуальные и общие индексы. Построение агрегатных индексов

 

Индексы сочетают элементы относительных и средних величин. Их используют в анализе динамики, выполнения задания и сравнения по объектам или территориям как правило сложных совокупностей, состоящих из непосредственно не суммарных элементов.

Динамические индивидуальные (одноэлементные) индексы характеризуют изменение уровня признака у отдельных единиц совокупности.

В них сравнивают цены (р), себестоимость единицы продукции(z), урожайность с 1 га (у), количество реализованной продукции одного вида (q), посевную площадь по каждой сельскохозяйственной культуре (П) за отчетный (1) и базисный (0) периоды.

Индивидуальные индексы в исследовании динамики явления определяют по формулам:

; ; ; ; .

 

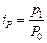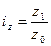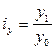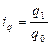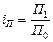Так, по данным таблицы 1 индексы цены и количества проданного товара А равны: ; .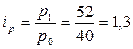

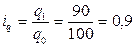Следовательно, цена товара выросла в 1,3 раза или на 30 % (1,3 * 100 = 130 %,

130 % – 100 % = +30 %), а объем его продажи уменьшился на 10 % (0,9 * 100 = 90 %,

90 % – 100 % = –10 %).

В расчете общих индексов используется вес (соизмеритель), с помощью которого преодолевается несуммарность элементов. В качестве веса выступает показатель, экономически связанный с индексируемым, т. е. их произведение дает величину, имеющую экономический смысл. Вес берется одинаковым (неизменным) в числителе и знаменателе индекса, индексируемая величина изменяется.

Так, в агрегатном индексе цен 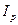изменяемой (индексируемой) величиной будет цена (Р₁ и Р₀), а весом будет количество товара, которое фиксируется на уровне отчетного периода времени (q₁):

.

По данным таблицы 1, 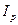равен:

 

 

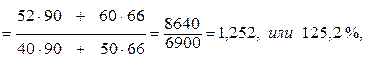
т. е. цены на товары А и Б выросли в 1,252 раза или на 25,2 % (1,252 * 100 = 125,2 %; 125,2 % – 100 % = 25,2 %).

Таблица 1

Показатели для расчета индексов цен и товарооборота в фактических и сопоставимых ценах

 

Товар	Цена за 1 кг (р.) за период	Продано за период (тыс. кг)	Индивидуальные индексы	Товарооборот за период (тыс. р.)
базисный, ро	отчетный, р1	базисный, q0	отчетный, q1	цен, iр	количества, iq	базисный, роqо	отчетный, p1q1	отчетный по базисным ценам, p0q1
А						0,9
Б					1,2	1,1
Итого	–	–	–	–	–	–

 

В агрегатном индексе физического объема (оборота в сопоставимых ценах) индексируемой величиной явлется количество товара (q₁ и q₀), весом (соизмерителем) – цена базисного периода :

По данным таблицы 1, он равен:

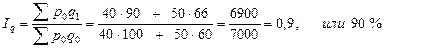
Следовательно, физическая масса проданных товаров в отчетном периоде в сравнении с базисным уменьшилась на 10 % (; 100 % – 90 % = –10 %).

 

Система индексов в исследовании факторов динамики объемных показателей

Индексы цен и физического объема применяют в факторном анализе динамики товарооборота во взаимосвязи с третьим индексом системы – индексом товарооборота в действующих ценах :

.

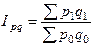По данным таблицы 1 индекс оборота (стоимости проданных товаров) в действующих ценах составляет:

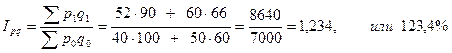
Следовательно, в отчетном периоде в сравнении с базисным оборот в действующих ценах увеличился на 23,4 %.

Система индексов имеет вид: 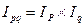, то есть 1,234 = 1,252 ´ 0,9. Ее используют для проверки правильности расчетов, а также для нахождения одного из индексов системы по двум известным. Так, индекс цен можно найти, поделив индекс товарооборота в действующих ценах на индекс физического объема (то есть товарооборота в сопоставимых ценах):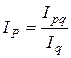 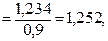а индекс физического объема – поделив индекс товарооборота в действующих ценах на индекс цен:

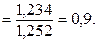
Индексную систему используют и для разложения абсолютных сумм прироста (уменьшения) исследуемого объемного показателя. Для этого из числителя каждого индекса вычитают его знаменатель.

Общий прирост товарооборота (Dрq) определяется по формуле:

Dрq = .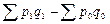

в том числе за счет

изменения цен: Dрq_(p) =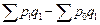

динамики физической массы: Dpq(_q)= .

По данным таблицы 1, они равны:

Dpq= );

Dpq(р)= ;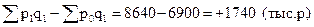

Dpq(q) =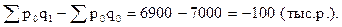

Следовательно, общий прирост товарооборота 1640 тыс. р. вызван ростом цен на 1740 тыс. р. и уменьшением физической массы проданных товаров на 100 тыс. р.

Общий прирост оборота равен сумме двух приростов: + 1640 = + 1740 + (–100)

или Dрq = Dpq(p) + Dpq(q).

Одновременно разность между числителем и знаменателем индекса цен показывает сумму экономии (переплат) населения за счет снижения (роста) цен. Так, в нашем примере население переплатило 1740 тыс. р., купив продукцию по более высоким ценам.

Таким образом, при построении индексной системы использованы правила:

Какова взаимосвязь между показателями, такова и связь между их индексами: ; .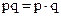

2. Веса сопряженных индексов берутся на уровне противоположных периодов времени.

Так, в индексе цен вес отчетного периода (q₁), а в индексе физического объема – базисного (р_о): . Только при таком взвешивании произведение этих индексов дает индекс товарооборота.

или .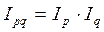

3. При разложении абсолютных разностей обязательно из числителя соответствующего индекса вычитается его знаменатель.

Аналогично строятся индексные системы других показателей. Например, индексная система затрат на производство продукции:

,

где I_zq– индекс общих затрат на производство,

z₀; z₁– себестоимость единицы продукции в базисном и отчетном периодах;

q₀; q₁ – количество продукции в базисном и отчетном периодах;

z₀q₀; z₁q₁ – затраты на производство продукции в базисном и отчетном периодах;

z₀q₁ – затраты отчетного периода при базисной себестоимости.

– общий индекс себестоимости;

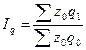– общий индекс физического объема продукции;

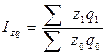– общий индекс затрат на производство.

Абсолютное изменение затрат на производство продукции рассчитывается как разность между числителем и знаменателем соответствующих индексов:

общее изменение затрат: Dzq = ,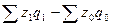

в том числе за счет изменения себестоимости:

Dzq(z)=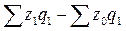

за счет динамики физического объема продукции:

Dzq(q) = .

Таким образом, Dzq = Dzq(z) + Dzq(q)