Проблема достоверности наших представлений об окружающем мире, т.е. проблема соответствия модели объекта и реального объекта, является ключевой проблемой в теории познания.
В настоящее время общепринято, что критерием истинности наших знаний является опыт. Модель адекватна объекту, если результаты теоретических исследований (расчёт) совпадают с результатами опыта (измерений) в пределах погрешности последнего.
Погрешности имеют место не только при измерениях, но и при теоретическом моделировании.
Для теоретических моделей, в соответствии с природой возникновения, будем различать:
– погрешности, возникающие при разработке физической модели;
– погрешности, связанные с приближениями при составлении математической модели;
– погрешности метода анализа математической модели;
– погрешности, связанные с конечным числом разрядов чисел при вычислениях.
Приведем пример: число 
в рамках символической записи как отношение длины окружности к диаметру представляет собой точное число, но попытка записать его в численном виде 
вызывает погрешность, связанную с конечным числом разрядов.
Эти перечисленные погрешности называются методическими. При измерениях методические погрешности проявляют себя как систематические.
Рассмотрим возможные погрешности математической модели на следующем примере:
Предположим, что физическая модель маятника такова:
– нить – невесома, нерастяжима;
– тело (масса) – материальная точка.
Тогда в рамках выбранной физической модели математическая модель маятника – уравнение движения маятника (рисунок 3.1) – будет иметь следующий вид:
(3.8)
При 
обычно считают, что 
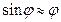, и тогда уравнение движения записывается:
(3.9)
Рисунок 3.7 – Графическая интерпретация физической модели маятника
Его решение имеет вид:
, (3.10)
где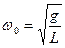 
Но при более точном решении (разложение в ряд Тейлора) предыдущего уравнения получим ω=ω0(1- φ02/16 +…).
Отсюда следует, что период колебаний маятника зависит от амплитуды колебаний.
Проблема построения и анализа математической модели с заданной точностью, а также оценка погрешности численных расчётов в ряде случаев очень сложна. Требуется высокая математическая культура исследователя, необходим тщательный математический анализ и самой модели, и применяемых методов решения.
Например, не имеет смысла требование решения уравнения с точностью, существенно превышающей точность построения физической модели.
Применение ЭВМ значительно увеличило возможности построения и исследования математических моделей в технике, однако не следует думать, что совершенное знание математики, численных методов и языков программирования позволит решить любую физическую и прикладную задачу. Дело в том, что даже самые изящные и точные методы расчетов не могут исправить ошибки, допущенные при построении физической модели.
