.
Пример 3-1. Определить среднее значение коэффициента теплоотдачи и количество передаваемой теплоты при течении воды вгоризонтальной трубке внутренним диаметром d = 3 мм и длиной ℓ = 0,5 м, если скорость воды
w = 0,3 м/с, средняя по длине трубы температура воды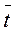 
ж = 60 0С и средняя температура стенки 
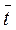= 20°С.
При 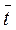=60 °C имеем: теплопроводность воды λж = 0,659 Вт/(м°C); кинематическая вязкость v ж = 0.478 . 10-6 м2/с; число Прантля Рrж = 2,98; при 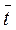c = 20°C число Прантля Ргс = 7,02.
Расчет проводим в следующей последовательности:
Критериальное уравнение
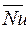dж = 1,4 (Redж d/ℓ)0.4 Рrж0.33 (Рrж / Ргс )0.25
Примечание :подстрочные индексы означают, что входящие в критерий физические свойства берутся при температуре жидкости «ж» или стенки»с», а характерный размер – диаметр «d»
Входящие в него сомножители
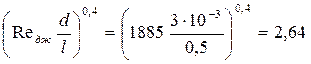
Рrж0.33 = 1,42 (Рrж / Ргс )0.25 = (2,98/7,02)0,25 = 0,81
Откуда:
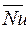dж = 1,4. 2,64.1,42.0,81=4,24
Коэффициент теплоотдачи
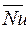= dж (λж/d) = 4,24 . (0,659 / 3.10-3 ) = 928 Вт/(м. 0С)
Количество передаваемой теплоты
Q=πdℓ ∆t= 3,14.3.10-3.0,5.928.40= 175 Вт.
Пример 3-2.
По трубе диаметром d = 60 мм и длиной ℓ = 2,1 м протекает воздух со скоростью w = 5 м/с. Определить значение среднего коэффициента теплоотдачи, если средняя температура воздуха 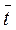ж = 100°С.
При 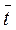ж= 100°С теплопроводность воздуха и его вязкость имеют следующие значения: λж = 0,0321 Вт/(м 0С), vж = 23,13 . 10-6 м 2/с
Число Рейнольдса
Redж = ωd/v= 5.0,06 / 23,13.10-6 = 12970
Redж 0.8 = 1955
Подставляя эти значения в критериальное уравнение, получаем:
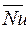dж = 0,018. 1955=35,2
откуда
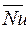= dж (λж /d) = 35,2 . (0,0321/0,06)=18,8 Вт/(м. 0С)
Так как ℓ/d = 2,1/0,06 = 35 < 50, то для короткой трубы необходимо ввести поправку на теплообмен во входном участке έℓ; из таблицы έℓ=1,04
Тогда окончательно получим
= έℓ = 18,8 . 1,04 = 19,5 Вт/(м 2. 0С)
Пример 3-3.
Через трубу теплообменника диаметром d = 50 мм и длинойℓ=3 м со скоростью w =0,8 м/с протекает вода. Определить средний коэффициент теплоотдачи, если средняя температура воды 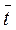ж = 50 0С, а температура стенки
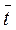с = 70 0С.
При 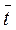ж = 50° С λж = 0,648 Вт/(м . °С); кинематическая вязкость
v ж = 5,56 . 10-7 м2/с и критерий (число) Прантля Ргж = 3.54
При 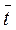c = 70 ° СРгс= 2,55;
Redж = (wd)/vж = (0,8. 0,05)/5,56 . 10-7 =7,2. 102; Redж0,8=7,7. 103
Рrж0.43 = 1,72; (Рrж / Ргс )0.25 = (3,54/2,55)0,25=1,09
Так как l/d = 60 > 50, то поправка на влияние длины трубыέℓ = 1. Подставляя сомножители в критериальное уравнение получаем:
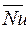dж =0,021 .7,7 .103.1,72 .1,09 .1=303
откуда
3920 Вт/(м 2. 0С)
Пример 3-4
Решением «сопряженной» задачи теплообмена получена зависимость теплового потока от толщины изоляции, выполненной из двух материалов с различной теплопроводностью (сопряженной называется задача, в которой тепловой поток, подводимый к стенке или отводимый от неё, находится совместно с решением уравнения теплопроводности для стенки). Из представленных в таблице и на рисунке данных видно, что увеличение толщины теплоизоляции не всегда приводит к уменьшению тепловых потерь (кривая 2). Это объясняется увеличением теплового потока, отбираемого с наружной поверхности теплоизоляции за счёт увеличения её поверхности с ростом наружного диаметра.
Таблица 1 Зависимость, теплового потока от толщины изоляции
δиз / .R2
δизм мм 
| 0.05 | 0,1 | 0,15 | 0,2 | 0,28 | 0,3 | 0,4 | 0,5 | 0,8 | 1,0 | ||
| 0,625 | 1,25 | 1,875 | 2,5 | 3,5 | 3,75 | 6,25 | 12,5 | |||||
| Qиз./Q | Асбест | 1,01 | 1,017 | 1,0217 | 1,0249 | 1,0266 | 1,026 | 1,024 | 1,017 | 0,986 | 0,960 | |
| Стекловата | 1 | 0,905 | 0,829 | 0,776 | 0,713 | 0,644 | 0,629 | 0,566 | 0,517 | 0,418 | 0,3 75 |
Рис, 8.10. Зависимость теплового потока от толщины цилиндрической изоляции:
а - цилиндрическая стенка с изоляцией; б - зависимость относительного теплового потока
Q из / Q от толщины изоляции 1- "хорошая" изоляция (стекловата);
2 - "плохая" изоляция (асбест)
