Теплопроводность цилиндрической стенки

I.. Однородная стенка. Рассмотрим однородную ци­линдрическую стенку (трубу) длиной ℓ, с внутренним радиусом r₁ и внешним r₂ . Коэффициент теплопроводности материала λ постоя­нен. Внутренняя и внешняя поверхности поддерживаются при по­стоянных температурах t₁ и t₂, причем t₁ > t₂, (рис. 1-11) и темпе­ратура изменяется только в радиальном направлении r. Следова­тельно, температурное поле здесь будет одномерным, а изотермиче­ские поверхности цилиндрическими, имеющими с трубой общую ось. Выделим внутри стенки кольцевой слой радиусом г и толщи­ной dr, ограниченный изотермическими поверхностями. Согласно закону Фурье, количество теплоты, проходящее в единицу времени через этот слой, равно:

 

Разделив переменные, имеем:

 

(б)

 

После интегрирования уравнения (б) находим:

 

(в)

Подставляя значения переменных на границах стенки (при r = r₁ t=t₁ и при r = r₂ t=t₂) и исключая постоянную С, полу­чаем следующую расчетную формулу:

 

 

(1-10)

Следовательно, количество теплоты, переданное в единицу вре­мени через стенку трубы, прямо пропорционально коэффициенту теплопроводности λ, длине ℓ и температурному напору ∆t = t₁ - t₂ и обратно пропорционально натуральному логарифму отношения внешнего диаметра трубы d2 к внутреннему d1. Формула (1-10) справедлива и для случая, когда t₁ < t₂, т. е. когда тепловой по­ток направлен от наружной поверхности к внутренней.

Количество теплоты, проходящее через стенку трубы, может быть отнесено либо к единице длины ℓ, либо к единице внутренней F1 пли внешней F2 поверхности трубы. При этом расчетные фор­мулы соответственно принимают следующий вид:

 

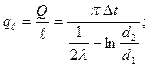(1-11)

 

(1-12)

 

 

 

 

(1-13)

 

 

Так как площади внутренней и внешней поверхностей трубы различны, то различными получаются и значения плотностей теп­ловых потоков q1 иq 2. Взаимная связь между ними определяется соотношением

или

Уравнение температурной кривой внутри однородной цилин­дрической стенки выводится из уравнения (в). Подставляя сюда значения Q и С имеем:

 

(1-14)

Следовательно, в этом случае при постоянном значении коэффи­циента теплопроводности λ температура изменяется по логарифмической кривой (рис. 1-11). С учетом зависимости коэффициента теплопроводности от температуры λ= λ_о (1 + bt ) уравнениетем­пературной кривой принимает следующий вид:

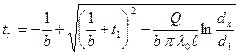(1-15)

 

2. М и о г о с л о й н а я с т е н к а. Пусть цилиндрическая стенка состоит из трех разнородных слоев. Диаметры и коэффици­ентытеплопроводности отдельных слоев известны, их обозначения см. на рис. 1-12. Кроме того, известны температуры внутренней

 

 

Рис. 1-11. Однородная цилиндрическая стенка. Рис. 1-12. Многослойная цилиндрическая стенка

 

! и внешней поверхностей многослойной стенки t₁ и t₄. В местах же соприкосновения слоев температуры неизвестны, обозначим их через t₁ и t₃.

При стационарном тепловом режиме через все слои проходит одно и то же количество теплоты. Поэтому на основании уравнения (1-11) можно написать:

 

(г)

 

Из этих уравнений определяется температурный напор вкаж­дом слое:

(д)

Сумма этих температурных напоров составляет полный темпера­турный напор. Складывая отдельно левые и правые части системы уравнении (д), имеем:

(е)

из этого уравнения определяем значение линейной плотности теп­лового потока q_ℓ:

(1-16)

 

По аналогии с этим сразу можно написать расчетную формулу для n-слойной стенки

 

(1-17)

 

 

Значения неизвестных температур t₂ и t₃ поверхностей сопри­косновения слоев определяются из системы уравнений (д):

(1-18)

 

 

Согласно уравнению (1-14), внутри каждого слоя температура изменяетсяпо логарифмическому закону, а для многослойной стенки в целом температурная кривая представляет собой лома­нуюкривую (рис. 1-12).

 

 

Конвективный теплообмен.

Физическая картина и определяющие параметры.

Конвективный теплообмен обусловлен движением жидкости около твердой поверхности. Различают свободную конвекцию, обусловленную гравитационными силами и вынужденную конвекцию, обусловленную перепадом давления.

Область, где имеется существенное изменение скорости динамики нагруженного слоя. Область температуры – температурный пограничный слой. Передача температуры в ламинарном потоке осуществляется механизмом теплопроводности, а в турбулентном – механизмом конвекции: . Толщина (d) зависит от текучести жидкости, её вязкости, температуры стенки, размеров и формы обтекания тела, практически не поддается расчету:

- формула Ньютона. a - удельный тепловой коэффициент потока в стенку при разности температур в 1°. .

 

 

Теория подобия.

Основные определения и понятия.

 

Теория подобия – отрасль знаний, позволяющая описывать одинаковыми уравнениями различные физические явления (например: перенос тепла, массы, электроэнергии).

Различают подобия:

_- Геометрическое, т.е. изучаемы объекты должны иметь одинаковую форму.

, где r – радиус изгиба, k_L – константа геометрического подобия (характерный линейный размер).

_- Кинематическое, характеризуется равным отношением скоростей в сходственных точках и равными углами между векторами скорости и направлением координат.

_- Динамическое, характеризуется постоянными константами сил, движущихся в сходственных точках, равными углами между векторами сил и координатными осями.

_- Тепловое, характеризуется равными температурными излучениями и одинаковым расположением изотерм. Теория подобия неразделима от теории размерности – все переменные делятся на размерные и безразмерные, а размерные делятся на первичные (масса, длина, время, температура) и производные (скорость, ускорение, работа, сила). Теория подобия оперирует комплексами размерных переменных, число которых может быть два и более. Эти комплексы имеют нулевую размерность. Если количество входящих три и более величин – критерий подобия. Критерии подобия могут быть получены главным образом с использованием системы уравнений сохранение массы и количества энергии, движения, описывающие физическое явление. Пример: используем уравнение Бернули.

 

 

Теплообмен в режиме вынужденной конвекции.

Обтекание плоской пластины.

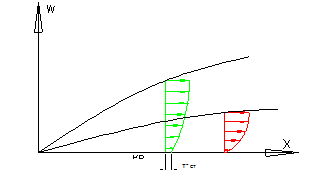Расчет теплообмена начинается с расчета задачи о пограничном слое.

 

Профиль скорости при решении задачи обычно задается w(y). Для ламинарного – это всегда степенная зависимость, а для турбулентного – степенная или логарифмическая зависимость.

 

При расчете теплообменников встречается задача об обтекании трубы или пучка труб.

Расположение труб:

_- Рядовое –

 

_- Шахматное -

 

 

Существует критериальное уравнение для обтекания одиночной трубы. Оно может быть использовано для обтекания первого ряда. Поскольку при обтекании первого ряда происходит турбулизация потока жидкости, то для второго ряда теплообмен усиливается. При обтекании третьего ряда ещё несколько усиливается.

S – поправочный коэффициент, y - коэффициент, учитывающий наклон трубы к вектору скорости потока (на рисунке они перпендикулярны).

 

Внутреннее обтекание тел.

Движение жидкости в круглых трубах. Наиболее часто встречается движение жидкости – турбулентное.

Толщина динамического и конвективного слоев практически равна.

 

Теплообмен излучением.

Характерен для теплозащитного покрытия двигателей. В производстве в тех. процессах роль теплообмена излучением велика там, где велика температура заготовок, сырья (металлургия, прокат, ковка, штамповка). Теплообмен излучением происходит без непосредственного контакта, между двумя телами, в том числе через вакуум. В зависимости от длины волны излучение может быть: рентгеновское, ультрафиолетовое, световое, инфракрасное (тепловое). Количество энергии, излучаемое с единицы поверхности тела в единицу времени называется его излучательной способностью.

Изобразим баланс энергий, где из всего падающего излучения часть отражается, часть поглощается, а часть проходит.

.

Если A=1,а R=0 и D=0 – тело называется абсолютно белым.

Если R=1, а A=0 и D=0 – тело называется абсолютно черным.

Если D=1, а A=0 и R=0 – тело называется абсолютно прозрачным.

Все тела в природе являются серыми 0<R<1. Пример: абсолютно черного тела – шар с маленьким отверстием, абсолютно белого – полированная металлическая поверхность, абсолютно прозрачного – одно и двух атомные газы. , где e - степень черноты тела – это отношение излучаемой энергии к энергии излучения абсолютно черного тела. e = 0,05 – полированный алюминий, а если произойдет окисление алюминия, то e = 0,8. Увеличение шероховатости поверхности ведет к увеличению черноты.

Наиболее важным для расчета излучения является закон Стефана-Больцмана, который связывает скорость потока энергии с температурой тела.

 

 

Т₁ > Т₂

- А – площадь пластины, e_ПР – приведенная степень черноты двух пластин.

 

 

Использование тепловых экранов.

Тепловые экраны применяется для снижения потерь тепла и для защиты элементов систем отнегативного воздействия повышенных температур

 

 

Знаменатель решим как сумму двух сопротивлений:

1) сопротивление поглощение первой стенки;

2) сопротивление испусканию этой стенкой. Каждый экран будет добавлять в знаменатель два слагаемых. Если предложить, что степень черноты экранов и стенок одинакова, то:

n – число экранов. Большое количество экранов использовать не рационально (1 - 2), они должны быть выполнены из материала с малой степенью черноты.

 

Теплообменные аппараты.

Классификация и типы теплообменных аппаратов.

1) рекуперативные (более частые);

2) регенеративные;

3) контактные (смесительные);

Теплообменный аппарат – аппарат, который служит для передачи тепла и характеризуется двумя и более теплоносителями.

I. Рекуперативные. Теплоносители не контактируют между собой непосредственно, а обмен теплом осуществляется через стенку, которая называется рабочей поверхностью. Например – кожух трубный – рекуперативный теплообменник.

Между трубами есть зазор, по которому циркулирует второй теплоноситель. В зависимости от направления движения теплоносителей теплообменники могут быть:

- с попутным движением;

- с противотоком;

- с перекрестным движением;

- со смешанным движением.

По конструкции рабочей поверхности:

- трубчатые;

- пластинчатые.

Трубы могут иметь ребрение. В рекуперативных теплообменниках может существовать промежуточный теплоноситель, циркулирующий по замкнутому контуру. Подобная схема, к примеру, применяется на АЭС, где теплоноситель, проходящий через активную зону реактора, нагревает сначала теплоноситель первого контура, который в свою очередьнагревает теплоноситель второго контура, непосредственно вращающий турбину.

II. Регенеративные. Одна и та же поверхность поочередно обматывается то горячим, то холодным теплоносителем. Рассмотрим схему регенеративного теплообменника с вращающимся насадком.

1 – корпус,

2 – вращающийся насадок,

3 – перегородка, разделяющая полости для горячего и холодного теплоносителя.

 

 

III. Смесительные. Теплообмен идет при непосредственном контакте двух теплоносителей, находящихся в различных агрегатных состояний. Парагазагенератор: пар-газ смешивается с водой, испаряет её, образуя рабочее тело, обладает большой работоспособностью. Проектная задача заключается в получении парогаза на возможно более коротком пути.

Вода под давлением форсунки подается в реактивное пространство, капли воды увлекаются газовым потоком и испаряются в нём, что позволяет уменьшить объем реактивного пространства.

 

Тепловой расчет рекуперативного теплообменника.

Существует два вида расчета: проектный и проверочный. Цель проектного расчета: определение рабочей площади при известных температурах и расходах теплоносителей. Цель проверочного расчета: определение температуры холодного теплоносителя при известных расходах температуры на входе.

 

 

Dt^’=t’₁ – t’₂ Dt”=t”₁ – t”₂ t”₂ ® t”₁ t”₂ < t”₁

 

В схеме с противотоком тепловой напор может быть реализован по сравнению со схемой 1 (попутное движение).

Тепловой процесс описывается: уравнением теплового баланса и уравнением теплопередачи.

Уравнение теплового баланса:

Уравнение теплопередачи:

Формула справедлива для схем 1,2

Для более сложных схем вводится поправочный коэффициент. Для схем теплообменников, где условия теплообмена существенно отличаются по площади: .

 

Гидравлический расчет для рекуперативного теплообменника.

Цель: определение мощности насоса или вентилятора, необходимой для подачи теплоносителя.

Dp = Dp_ж + Dр_труб +Dр_{теплообм}.

 

Используется для газообразных теплоносителей.

- скоростной тепловой напор.

 

Контрольное задание заочникам и примеры задач

Термодинамика

1.1. Изобразите все известные вам термодинамические процессы в p-V и T-S координатах, Сведите в таблицу формулы для расчёта внутренней энергии, энтальпии, технической работы и энтропии для каждого из процессов. Укажите площади под кривыми процессов, соответствующие подведённому теплу, технической работе, работе расширения, изменению внутренней энергии.

1.2. Изобразите в координатах p-V и T-S диаграмму получения перегретого водяного пара с указанием количества затраченного тепла на всех этапах его получения.

 

Теплопроводность

Разберите приведённые ниже примеры решения задач, решите задачи № 2.1 и 2.3 для исходных данных, соответствующих номеру вашего варианта.