Индивидуалные задания первого уровня

Условия к заданиям:

1. A, B - некоторые множества, ય - универсальное множество. Найдите AÇB, AÈB, A\B, B\A, A¢, B¢, A¢DB.

2. На диаграмме Эйлера отметьте области, соответствующие данному множеству X.

3. Упростите теоретико-множественные выражения, данные в задаче 2.

4. Высказывание задано формулой F. Удалите все возможные скобки так, чтобы получилось высказывание, равносильное исходному. Затем расставьте приоритет выполнения операций и постройте таблицу истинности данного высказывания.

5. Упростите данную формулу исчисления высказываний.

6. P(x), T(x,y) - предикаты, определенные на множестве A. Найдите области истинности данных предикатов.

7. Найдите область истинности предиката P(x), определенного на множестве действительных чисел.

8. F - соответствие из A в B. Проверьте выполнимость свойств соответствия (всюду определенность, однозначность, соответствие «на», разнозначность). Выясните, является ли данное соответствие отображением.

9. F - отображение из A в B. Проверьте выполнимость свойств отображения (сюръективность, инъективность, биективность).

10. r - бинарное отношение, определенное на множестве M. Проверьте выполнимость свойств бинарного отношения (рефлексивность, симметричность, транзитивность, антирефлексивность, антисимметричность, линейность) r.

Вариант 1

1. 1) A = {2, 5, 4, 6, 7, 1}, B = {1, 4, 8, 9, 5}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (-2; 9), B = (-¥; 0], ય = R.

2. 1) X = (A\B)¢ÇA; 2) X = ((A¢ \(C\B)¢)Ç(B\C).

3. См. пункт 2.

4. (((ù X) ® (ù (Z ® (ù Y)))) & (X ® Y))

5. X & ù Z ® (X «ù Y)

6. A = {0, -1, 3, 5, 4, 1}; P(x) = «x ³ 3»; T(x,y) = «x - натуральный делитель числа y».

7. P(x) = «».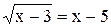

8. 1) A = {2, 5, 4, 6}, B = {1, 8, 9, 5}, F = {(5,5), (4,1), (6,8), (2,9)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç x-y - четное число}.

9. A = N (множество натуральных чисел); B = R (множество действительных чисел); "xÎA F(x) = 7x²-2x+1.

10. M = Z (множество целых чисел). Бинарное отношение r задано по правилу: a r b Û (a + 1)b кратно 10.

Вариант 2

1. 1) A = {1, 5, 3, 7, 8}, B = {4, 8, 1, 6}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = [12; +¥), B = (-3; 20], ય = R.

2. 1) X = AÇ(B\AÈB); 2) X = (AÈB¢)¢ È(C¢ \B)¢.

3. См. пункт 2.

4. (((Y & (ù X)) ® (ù Z)) ® (Y ® Z))

5. (X & ù Z ® Z V ù Y) ® X

6. A = {2, 1, 0, 4, 5}; P(x) = «x - простое число»; T(x,y) = «x+2y - делится на 3».

7. P(x) = «2çx-1ç+çx+3ç=10».

8. 1) A = {1, 3, 6, 8}, B = {4, 1, 6}, F = {(3,4), (1,6), (8,1), (6,4)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç x - делитель числа y}.

9. A = B = Q (множество рациональных чисел); "xÎA F(x) = ÷ x+2÷-4.

10. M - множество точек плоскости. На плоскости задана фиксированная окружность a. Бинарное отношение r задано по правилу: A r B Û через точки A и B можно провести прямую, пересекающую a.

Вариант 3

1. 1) A = {3, 4, 7, 2}, B = {9, 1, 2, 5, 3}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = [-13; -1), B = (-10; 10), ય = R.

2. 1) X = A¢\B È(BÇA)¢; 2) X = (CÇB)\(AÈB¢ \C)¢.

3. См. пункт 2.

4. (X ® (ù ((X V Z) ® (ù Y))))

5. ù (ù X V ù Y) ® ù (X & Z ® ù Y)

6. A = {1, 3, 7, 2}; P(x) = «x²-5x > 0»; T(x,y) = «x-y - положительное четное число».

7. P(x) = «».

8. 1) A = {4, 3, 9, 6}, B = {8, 6, 4, 3, 5}, F = {(3,5), (9,8), (4,4), (6,3)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç x - остаток от деления y на 3}.

9. A = Q⁺ (множество положительных рациональных чисел); B = R (множество действительных чисел); "xÎA F(x) = ln x+5.

10. M = N (множество натуральных чисел). Бинарное отношение r задано по правилу: a r b Û каждая цифра числа a меньше всех цифр числа b.

 

Вариант 4

1. 1) A = {2, 4, 6, 7, 9}, B = {1, 4}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (-¥; 9), B = (-3; +¥), ય = R.

2. 1) X = ((A¢ÇB)\A¢)¢; 2) X = AÈ((BÈC)ÇC¢)ÇB.

3. См. пункт 2.

4. (((X & (Y ® Z)) V Y) ® (ù X))

5. (X «ù Y) & Z ® ù X

6. A = {2, 1, 5}; P(x) = «3x+5 делится на 4»; T(x,y) = «xy - простое число».

7. P(x) = «2ç3x-1ç<4».

8. 1) A = {1, 3, 4, 9}, B = {4, 9, 1, 6}, F = {(3,1), (1,6), (9,6), (4,1)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç x - произведение первой и последней цифр числа y}.

9. A = B = R (множество действительных чисел); "xÎA F(x) = 3+2e^x+4.

10. M = Z (множество целых чисел). Бинарное отношение r задано по правилу: a r b Û |a + b| = b².

Вариант 5

1. 1) A = {3, 2, 4, 6, 8}, B = {2, 8, 1, 9, 4, 3}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (-7; 92], B = [-1; 100), ય = R.

2. 1) X = (A\B¢)¢ È(AÇB); 2) X = BÈ(CÈA¢)Ç(A\B)¢.

3. См. пункт 2.

4. (((X ® Y) ® Z) ® (ù Y))

5. X & Y ® (X V Z) ® ù Y

6. A = {4, 3, 0}; P(x) = «sin x > 0»; T(x,y) = «x²-3y = 0».

7. P(x) = «».

8. 1) A = {4, 3, 5, 9}, B = {5, 9, 3, 7, 4}, F = {(4,4), (5,7), (9,3), (5,9), (3,5)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç y = 2x-3}.

9. A = Q⁺ (множество положительных рациональных чисел); B = R (множество действительных чисел); "xÎA F(x) = .

10. M - множество точек плоскости. На плоскости заданы две фиксированные точки О₁ и О₂. Бинарное отношение r задано по правилу: A r B Û AO₁ = BO₂.

Вариант 6

1. 1) A = {3, 9, 4, 6, 1}, B = {1, 8, 9, 5, 7}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = [2; 22], B = (-¥; 10), ય = R.

2. 1) X = A¢È(AÇB\A); 2) X = (CÇA)È(B¢ \C)ÇA\C.

3. См. пункт 2.

4. ((Y & Z) «(((ù X) V Z) V (ù Y)))

5. X & ù Y V Z ® (Y ® Z)

6. A = {0, 2, 4, -4}; P(x) = «x-2 > 0»; T(x,y) = «Точка M(x,y) лежит внутри круга с центром в точке (0,0) радиуса 4».

7. P(x) = «ç2x+1ç-2çx-4ç=1».

8. 1) A = {4, 1, 5, 8}, B = {5, 1, 4}, F = {(4,4), (5,1), (8,4), (5,5), (1,5)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç x²+y² = 9}.

9. A = N (множество натуральных чисел); B = R (множество действительных чисел); "xÎA F(x) = 4+sin(x+2).

10. M = N (множество натуральных чисел). Бинарное отношение r задано по правилу: a r b Û a кратно b².

Вариант 7

1. 1) A = {2, 7, 1}, B = {1, 8, 4, 6, 7, 9, 5}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (-¥; 34], B = [20; +¥), ય = R.

2. 1) X = BÈ(AÈ(BÇA))¢; 2) X = (C\B)ÇA¢ È(A\C)¢.

3. См. пункт 2.

4. ((ù (Z ® X)) ® (ù (Y & X)))

5. ù Y® X & ù Z ® ù X V Y

6. A = {4, 0, -2, 3}; P(x) = «(x+2)(x-3) ¹ 0»; T(x,y) = «x кратно 2y».

7. P(x) = «».

8. 1) A = {3, 1, 2, 9}, B = {3, 5, 8, 7, 2, 4}, F = {(1,4), (9,5), (2,7), (3,3), (1,8)};

2) A = B = N (множество натуральных чисел); F = {(x,y) çесли x>5, то y = x, иначе y = 4x-1}.

9. A = Z⁺ (множество положительных целых чисел); B = R (множество действительных чисел); "xÎA F(x) = .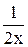

10. M - множество точек плоскости. На плоскости задана фиксированная прямая a. Бинарное отношение r задано по правилу: A r B Û через точки A и B можно провести прямую перпендикулярную a.

Вариант 8

1. 1) A = {1, 2, 6, 4, 7}, B = {4, 8, 2, 5}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (-11; +¥), B = [-22; 30], ય = R.

2. 1) X = A\BÇ(BÇA¢)ÈA; 2) X = ((CÈB)ÇA¢)¢ ÈC\B.

3. См. пункт 2.

4. ((ù (Y ®ù Z)) V (ù (Y & X)))

5. ù (X®ù Z)® ((X V Z) & ù Y)

6. A = {0, -3, -2, -4}; P(x) = «x³+8 < 0»; T(x,y) = «x+yÎ[-2; 0]».

7. P(x) = «4ç3-2xç>2».

8. 1) A = {4, 2, 8, 7}, B = {1, 4, 2, 5}, F = {(7,4), (2,5), (2,4), (4,2), (8,2)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç x делится на y}.

9. A = Z (множество целых чисел); B = R (множество действительных чисел); "xÎA F(x) = 3x²-x+3.

10. M = N (множество натуральных чисел). Бинарное отношение r задано по правилу: a r b Û каждая цифра числа a равна некоторой цифре числа b.

Вариант 9

1. 1) A = {9, 8, 5, 7, 1}, B = {1, 8, 4, 5, 6, 7}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = [-2; +¥), B = [7; 10), ય = R.

2. 1) X = B¢ È(A\B)¢ÇA; 2) X = A¢ \(AÇB)Ç(CÈB)¢.

3. См. пункт 2.

4. ((((ù X) V (ù Y)) & (ù X)) ® (ù Z))

5. (X ® ù (Y V Z)) ® ù X

6. A = {0, 4, -4}; P(x) = «x - корень уравнения a²-4a+4 = 0 (a - переменная)»; T(x,y) = «Точка M(x,y) принадлежит окружности с центром (-1, 0) радиуса 3».

7. P(x) = «».

8. 1) A = {3, 4, 2, 9, 8, 1}, B = {1, 7, 2, 6}, F = {(4,1), (2,7), (9,6), (8,2)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç 2x+y - нечетное число}.

9. A = Z (множество целых чисел); B = Q (множество рациональных чисел); "xÎA F(x) = ÷ x-2÷/4.

10. M = N (множество натуральных чисел). Бинарное отношение r задано по правилу: a r b Û a² + b² = 50.

Вариант 10

1. 1) A = {5, 7, 9, 3}, B = {1, 7, 9, 4, 8, 2}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = [-32; 48), B = [5; 60], ય = R.

2. 1) X = A\(B¢ÇA)ÈA; 2) X = (AÇC¢)¢È(BÈA\C).

3. См. пункт 2.

4. ((ù Y) ® ((ù (X ® Y)) V (ù (X & (ù Z)))))

5. (ù (Y ® Z) ® ù (Z & ù X)) & ù Y

6. A = {5, 4, -3, 1, -8}; P(x) = «çx-4ç - простое натуральное число»; T(x,y) = «x² = y³».

7. P(x) = «ç3x+10ç-3=çx+3ç».

8. 1) A = {1, 4, 5, 8, 6}, B = {4, 1, 2}, F = {(1,1), (5,4), (6,4), (8,2)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç y - неполное частное от деления x на 8}.

9. A = N (множество натуральных чисел); B = R (множество действительных чисел); "xÎA F(x) = log₃(x+2).

10. M - множество точек плоскости. На плоскости заданы две фиксированные точки О₁ и О₂. Бинарное отношение r задано по правилу: A r B Û AO₁ = 2BO₂.

Вариант 11

1. 1) A = {1, 3, 2, 5, 4, 6}, B = {4, 1, 8, 9, 6}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (4; 19), B = (-¥; 10), ય = R.

2. 1) X = BÇ(AÈB¢)¢ \A; 2) X = A\B¢ Ç(AÈC)\B.

3. См. пункт 2.

4. ((Z ® ((ù X) & Y)) & (Y V (ù (Y ® (ù Z)))))

5. (ù Y ® ù Z) & (X ® Y & ù X)

6. A = {p+2, , , 2}; P(x) = «Число x - рациональное»; T(x,y) = «».

7. P(x) = «».

8. 1) A = {8, 9, 1, 5, 6}, B = {3, 4, 6, 2, 7}, F = {(1,3), (5,4), (6,2), (9,7)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç y - результат вычитания числа x из суммы цифр числа x}.

9. A = Q (множество рациональных чисел); B = R (множество действительных чисел); "xÎA F(x) = -4+6^x-3.

10. M = N (множество натуральных чисел). Бинарное отношение r задано по правилу: a r b Û a³ кратно b².

Вариант 12

1. 1) A = {7, 4, 2, 5, 6}, B = {1, 9, 4, 7}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (-18; 91], B = (-3; +¥), ય = R.

2. 1) X = (A\B)¢ÈA¢ÇB; 2) X = B\CÈ(A\B)ÇA\B¢.

3. См. пункт 2.

4, (((ù Y) & (ù X)) ® (ù (Y V Z)))

5. ù (X ® ù Z) & ù (Y ® (X ® Z))

6. A = { , , -1, }; P(x) = «»; T(x,y) = «x+y - целое число».

7. P(x) = «ç4x-6ç£10».

8. 1) A = {9, 1, 2, 6, 8}, B = {4, 1, 2, 8, 7}, F = {(9,1), (2,8), (6,1), (8,7)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç y = x²-3x+8}.

9. A = N (множество натуральных чисел); B = R (множество действительных чисел); "xÎA F(x) = .

10. M = N (множество натуральных чисел). Бинарное отношение r задано по правилу: a r b Û каждая цифра числа a меньше некоторой цифры числа b.

Вариант 13

1. 1) A = {3, 2}, B = {1, 3, 5, 7, 4, 9, 2}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (-¥; 79), B = [-5; +¥), ય = R.

2. 1) X = (BÇA¢)È(B\A); 2) X = B\A¢Ç(A\C¢)ÇB.

3. См. пункт 2.

4. (((ù X) ® (ù Y)) & ((ù Z) V Y))

5. (X ® ù (Y ® ù Z)) ® ù (X & Y)

6. A = {3, , 6}; P(x) = «çx-5ç+çx+3ç=3»; T(x,y) = « - целое число».

7. P(x) = «».

8. 1) A = {2, 8, 1, 4, 7}, B = {1, 4, 8, 7}, F = {(1,8), (8,4), (4,1), (1,7)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç (x-1)²+y² ³ 4}.

9. A = Q (множество рациональных чисел); B = R (множество действительных чисел); "xÎA F(x) = 4-3×sin x.

10. M - множество точек плоскости. На плоскости задана фиксированная прямая a. Бинарное отношение r задано по правилу: A r B Û Отрезок AB имеет общие точки с прямой a.

Вариант 14

1. 1) A = {8, 2, 9, 5, 6}, B = {8, 9, 4, 6, 5, 1}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (-4; +¥), B = (-15; 0), ય = R.

2. 1) X = A¢È(BÇA)\B; 2) X = C\((BÇA)ÈC)¢ È(A\C).

3. См. пункт 2.

4. (X ® ((ù Y) ® (Z & (ù X))))

5. ù Z V (X ® ù (Z V Y) & (X ® Y))

6. A = {6, 4, 3}; P(x) = «x+3 кратно x»; T(x,y) = «-x+2y - корень уравнения ».

7. P(x) = «çx-8ç-4çx+3ç+39=0».

8. 1) A = {2, 1, 5, 8, 7}, B = {2, 1, 4, 5}, F = {(1,1), (8,4), (2,2), (1,5), (8,1)};

2) A = B = N (множество натуральных чисел); F = {(x,y) çесли x делится на 2, то y = 3x, иначе y = x²}.

9. A = R⁺ (множество положительных действительных чисел); B = R (множество действительных чисел); "xÎA F(x) = .

10. M = Z (множество целых чисел). Бинарное отношение r задано по правилу: a r b Û |a + b| = -b.

Вариант 15

1. 1) A = {9, 2, 7, 1, 3, 5}, B = {5, 1, 8, 7, 9}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = [-12; 29], B = (4; 70], ય = R.

2. 1) X = (BÈA)Ç(B\A¢); 2) X = ((C\B)ÈA)È(AÇB¢)¢.

3. См. пункт 2.

4. ((X & (ù Z)) ® (X «(ù Y)))

5. (ù X ® ù (Z ® ù Y)) & (X ® Y)

6. A = {0, -1, 15}; P(x) = «-3< x £ 12»; T(x,y) = «x делит y+1».

7. P(x) = «».

8. 1) A = {5, 2, 6, 7, 4}, B = {1, 8, 4, 7, 5, 9}, F = {(6,1), (5,4), (4,8), (5,5), (2,7)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç y - делитель числа x}.

9. A = B = N (множество натуральных чисел); "xÎA F(x) = x²-2x+2.

10. M - множество точек плоскости. На плоскости заданы две фиксированные точки О₁ и О₂. Бинарное отношение r задано по правилу: A r B Û AO₁ < BO₂.

Вариант 16

1. 1) A = {6, 4, 2, 5, 9, 1}, B = {9, 3, 1, 8}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (-¥; 93], B = [8; 110], ય = R.

2. 1) X = AÈ(B\AÇA)¢; 2) X = (A¢ÇB)\(A\C)ÈB¢.

3. См. пункт 2.

4. (X «((Y & (ù Z)) ® (Z V (ù Y))))

5. ((Y & ù X) ® ù Z) ® (Y ® Z)

6. A = {1, -3}; P(x) = «5x > çx+2ç»; T(x,y) = «2x+y - отрицательное нечетное число».

7. P(x) = «4çx-2ç³3».

8. 1) A = {3, 4, 1, 7}, B = {9, 1, 4, 7, 2}, F = {(1,7), (3,4), (4,7), (3,9)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç 2x-3y - четное число}.

9. A = Z (множество целых чисел); B = N (множество натуральных чисел); "xÎA F(x) = 3÷ x-5÷+2.

10. M = N (множество натуральных чисел). Бинарное отношение r задано по правилу: a r b Û первая цифра числа a меньше, либо равна некоторой цифре числа b.

Вариант 17

1. 1) A = {6, 7, 1}, B = {1, 5, 4, 7, 2}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = [-9; 33), B = (-1; +¥), ય = R.

2. 1) X = (A¢ÇB¢)È(B\A); 2) X = (C\((BÇA)¢ÇA))¢ÈC.

3. См. пункт 2.

4. ((ù ((ù X) V (ù Y))) ® (ù ((X & Z) ® (ù Y))))

5. X ® ù ((X V Z) ® ù Y)

6. A = {1, 5, 13, 15}; P(x) = «x+11 делится на 6»; T(x,y) = «x - простой делитель числа y».

7. P(x) = «».

8. 1) A = {1, 5, 3, 8}, B = {2, 4, 9, 5}, F = {(5,5), (3,2), (8,4), (1,9)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç y - остаток от деления x на 4}.

9. A = N (множество натуральных чисел); B = R (множество действительных чисел); "xÎA F(x) = 3×lg(4x+2).

10. M = N (множество натуральных чисел). Бинарное отношение r задано по правилу: a r b Û ab² кратно 12.

Вариант 18

1. 1) A = {1, 4, 5, 9, 2, 7, 8}, B = {1, 2, 4, 9}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (-12; 78), B = [-3; +¥), ય = R.

2. 1) X = BÇ(AÈB¢)\B¢; 2) X = (C¢ \B)Ç(A\B)¢ ÈC.

3. См. пункт 2.

4. (((X «(ù Y)) & Z) ® (ù X))

5. X & (Y ® Z) V Y ® ù X

6. A = {-2, -1, 0}; P(x) = «x+3 - простое число»; T(x,y) = «çxç-3y кратно 5».

7. P(x) = «-2ç3x+1ç+ç-x+4ç=1».

8. 1) A = {4, 2, 6, 1}, B = {4, 2, 9}, F = {(2,4), (4,9), (1,2), (6,4)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç y - квадрат первой цифры числа x}.

9. A = Z (множество целых чисел); B = R (множество действительных чисел); "xÎA F(x) = 7-4×3^x.

10. M - множество точек плоскости. На плоскости задана фиксированная прямая a. Бинарное отношение r задано по правилу: A r B Û прямая a проходит через внутреннюю точку отрезка AB.

 

Вариант 19

1. 1) A = {3, 5, 1, 4}, B = {7, 1, 4, 8, 6}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (32; 97], B = (-4; 70), ય = R.

2. 1) X = (A¢ÇB¢)\(A\B¢); 2) X = CÇ((A¢ÈB)ÇC)\B¢.

3. См. пункт 2.

4. (((X & Y) ® (X V Z)) ® (ù Y))

5. ((X ® Y) ® Z) ® ù Y

6. A = { , 0, }; P(x) = «»; T(x,y) = «sin x-3y = 0».

7. P(x) = «».

8. 1) A = {8, 2, 9, 7}, B = {1, 6, 2, 3, 4}, F = {(2,4), (9,1), (8,2), (7,3)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç y = 4x+8}.

9. A = R⁺ (множество положительных действительных чисел); B = R (множество действительных чисел); "xÎA F(x) = .

10. M = N (множество натуральных чисел). Бинарное отношение r задано по правилу: a r b Û a² + b² = 37.

Вариант 20

1. 1) A = {6, 7, 9, 2, 1}, B = {5, 1, 8, 2, 9}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = [-52; +¥), B = (-¥; 60), ય = R.

2. 1) X = B¢ È(A¢Ç(A\B)); 2) X = (A\C)¢ Ç(CÇB)ÈC¢.

3. См. пункт 2.

4. (((X & (ù Y)) V Z) ® (Y ® Z))

5. Y & Z «ù X V Z V ù Y

6. A = {0, 2, -3}; P(x) = «-3x+2 > x²»; T(x,y) = «Точка M(x,y) лежит во второй четверти декартовой плоскости».

7. P(x) = «3ç4-2xç<4».

8. 1) A = {8, 3, 5, 1}, B = {5, 8, 1, 2}, F = {(3,1), (8,2), (1,2), (5,1)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç y² ³ x²}.

9. A = Z (множество целых чисел); B = R (множество действительных чисел); "xÎA F(x) = -2×sin(2x).

10. M - множество точек плоскости. На плоскости заданы две фиксированные точки О₁ и О₂. Бинарное отношение r задано по правилу: A r B Û 2AO₁ = BO₂.

Вариант 21

1. 1) A = {9, 2, 7, 5}, B = {2, 6, 1, 4, 8, 5, 9}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (2; +¥), B = (-5; 10], ય = R.

2. 1) X = (B\A)Ç(B¢ \A)¢; 2) X = (C¢ \B¢)È(AÈBÇA).

3. См. пункт 2.

4. (((ù Y)® (X & (ù Z))) ® ((ù X) V Y))

5. ù (Z ® X) ® ù (Y & X)

6. A = {7, 8, -3}; P(x) = «(x+3)(x²-7) = 0»; T(x,y) = «3x кратно -4y».

7. P(x) = «».

8. 1) A = {1, 3, 6, 2}, B = {1, 9, 3, 6, 4}, F = {(1,4), (6,6), (2,3), (6,9), (3,1)};

2) A = B = N (множество натуральных чисел); F = {(x,y) çесли x Î (-¥; -5) È [0; 4), то y = 5x+1, иначе y = x+1}.

9. A = N (множество натуральных чисел); B = R (множество действительных чисел); "xÎA F(x) = .

10. M = N (множество натуральных чисел). Бинарное отношение r задано по правилу: a r b Û последние цифры чисел a и b равны.

Вариант 22

1. 1) A = {1, 3, 2, 4, 9, 6, 7}, B = {4, 7, 8, 9}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = [-28; 45], B = (-¥; 10], ય = R.

2. 1) X = A\B¢ È(AÇB); 2) X = ((CÈB)Ç(A\B)ÈC¢)¢.

3. См. пункт 2.

4. ((ù (X®(ù Z)))® ((X V Z) & (ù Y)))

5. X V (Z & ù Y) ® ù X V Z

6. A = {2, -1, 1}; P(x) = «x³-1 ³ 0»; T(x,y) = «Точка M(x,y) принадлежит прямой, проходящей через точку (4, 1) параллельно оси абсцисс».

7. P(x) = «ç3x+11ç-2çx-2ç+3 = 0».

8. 1) A = {9, 2, 4, 8}, B = {5, 3, 9}, F = {(9,9), (4,3), (8,9), (4,5), (2,5)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç y делится на x}.

9. A = B = R (множество действительных чисел); "xÎA F(x) = = 4x²+2x-5.

10. M = Z (множество целых чисел). Бинарное отношение r задано по правилу: a r b Û (a + 3)b кратно 8.

 

Вариант 23

1. 1) A = {3, 7, 8, 4, 1}, B = {4, 9, 1, 5, 3}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (-¥; 88], B = [-5; 90), ય = R.

2. 1) X = (AÈB)ÈA¢ \B¢; 2) X = (CÈ(A¢ \B))¢ Ç(AÇC).

3. См. пункт 2.

4. ((X ® (ù (Y V Z))) ® (ù X))

5. (ù X V ù Y) & ù (X ® ù Z)

6. A = {1, -4}; P(x) = «3x - корень уравнения a²-2a-3 = 0»; T(x,y) = «xy Î (-4; +¥)».

7. P(x) = «».

8. 1) A = {3, 1, 7, 4}, B = {1, 5, 6, 7, 2, 3}, F = {(1,3), (4,5), (7,7), (3,1), (1,6)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç y-4x - нечетное число}.

9. A = B = R (множество действительных чисел); "xÎA F(x) = = 3÷ 4x+1÷-6.

10. M - множество точек плоскости. На плоскости задана фиксированная прямая a. Бинарное отношение r задано по правилу: A r B Û через точки A и B можно провести прямую параллельную a.

 

Вариант 24

1. 1) A = {8, 6, 2, 5}, B = {9, 7, 4, 8, 5}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (-¥; 47), B = [-6; 90], ય = R.

2. 1) X = AÇB¢ È(A\B); 2) X = (AÈC)¢ Ç(B\AÈC¢).

3. См. пункт 2.

4. (((ù (Y ® Z)) ® (ù (Z & (ù X)))) & (ù Y))

5. ù Y ® ù (X ® Y) V ù (X & ù Z)

6. A = {4, 3, 6}; P(x) = «3x+2 - простое число»; T(x,y) = «2x² = 3y».

7. P(x) = «ç4x+1ç>4».

8. 1) A = {9, 6, 8, 1}, B = {3, 4, 1, 5}, F = {(1,4), (6,5), (6,4), (9,1), (8,1)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç x - неполное частное от деления y на 6}.

9. A = R⁺ (множество положительных действительных чисел); B = R (множество действительных чисел); "xÎA F(x) = 4-log₅ x.

10. M = N (множество натуральных чисел). Бинарное отношение r задано по правилу: a r b Û a³ = b².

 

Вариант 25

1. 1) A = {6, 2, 4, 7, 9, 1}, B = {8, 1, 4, 9, 7}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = [-13; +¥), B = (-6; +¥), ય = R.

2. 1) X = BÈ(AÇB)¢ \A¢; 2) X = ((BÈA)ÇC¢)¢ \A¢.

3. См. пункт 2.

4. (((ù Y) ® (ù Z)) & (X ® (Y & (ù X))))

5. (Z ® ù X & Y) & (Y V ù (Y ® ù Z))

6. A = { , , 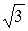}; P(x) = «Число x - иррациональное»; T(x,y) = «».

7. P(x) = «».

8. 1) A = {7, 4, 2, 3, 8, 5}, B = {4, 8, 2, 1}, F = {(4,4), (2,8), (3,1), (8,2)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç x - суммы всех цифр числа y и самого числа y}.

9. A = N (множество натуральных чисел); B = R (множество действительных чисел); "xÎA F(x) = 2^1-3x.

10. M - множество точек плоскости. На плоскости заданы две фиксированные точки О₁ и О₂. Бинарное отношение r задано по правилу: A r B Û отрезки AO₁ и BO₂ пересекаются.

Вариант 26

1. 1) A = {4, 5, 8, 1, 2, 6, 7}, B = {7, 9, 1, 5}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (-7; 14], B = (-¥; 6], ય = R.

2. 1) X = B\(AÈB¢)¢ÇA; 2) X = CÇ(A¢ ÈB)Ç(C\B)¢.

3. См. пункт 2.

4. ((ù (X ® (ù Z))) & (ù (Y ® (X ® Z))))

5. ù Y & ù X ® ù (Y V Z)

6. A = {2, , -1}; P(x) = «»; T(x,y) = «2x-y - натуральное число».

7. P(x) = «-çx-1ç+2ç3x+2ç=15».

8. 1) A = {2, 4, 7, 9, 1}, B = {9, 1, 5}, F = {(2,1), (7,9), (1,9), (9,5)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç y = 3x²+x-1}.

9. A = Z⁺ (множество положительных целых чисел); B = R (множество действительных чисел); "xÎA F(x) = .

10. M = N (множество натуральных чисел). Бинарное отношение r задано по правилу: a r b Û ab² кратно 54.

 

Вариант 27

1. 1) A = {7, 3, 2, 5}, B = {1, 8, 6, 9, 5, 3, 4}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = (-32; 79), B = (-4; 85], ય = R.

2. 1) X = ((BÈA)ÇA¢)¢ ÇB; 2) X = (C¢ ÇB)\((AÈB)¢ \C).

3. См. пункт 2.

4. ((X ® (ù (Y ® (ù Z)))) ® (ù (X & Y)))

5. (ù X ® ù Y) ® (ù Z V Y)

6. A = {4, 3, 8}; P(x) = «çx+2ç-çx-4ç=6»; T(x,y) = « - целое число».

7. P(x) = «».

8. 1) A = {4, 2, 1, 7, 3}, B = {1, 4, 5, 2, 9}, F = {(1,1), (7,4), (3,2), (2,9)};

2) A = B = N (множество натуральных чисел); F = {(x,y) ç x²+y² < 4}.

9. A = B = R (множество действительных чисел); "xÎA F(x) = = 3-sin(x+5).

10. M - множество точек плоскости. На плоскости задана фиксированная окружность a. Бинарное отношение r задано по правилу: A r B Û Отрезок AB имеет общие точки с окружностью a.

Вариант 28

1. 1) A = {5, 6, 1}, B = {8, 2, 1, 5, 4, 9, 3}, ય = {1, 2, 3, 4, 5, 6, 7, 8, 9};

2) A = [-3; 59], B = (-18; 40), ય = R.

2. 1) X = BÇ(A\B)ÇA¢; 2) X = CÇ(A¢ \B)¢ È(AÈC).

3. См. пункт 2.

4. ((ù Z) V (X ® ((ù (Z V Y)) & (X ® Y))))

5. ù X V Y ® (ù Y ® Z)

6. A = {2, 4, 3}; P(x) = «2x-5 делит x»; T(x,y) = «y-x - корень уравнения ».

7. P(x) = «5ç3-4xç£14».

8. 1) A = {5, 3, 2, 9, 4}, B = {5, 3, 2, 8, 1}, F = {(5,3), (2,8), (9,3), (4,1)};

2) A = B = N (множество натуральных чисел); F = {(x,y) çесли x - простое число, то y = 2x, иначе y = 4x}.

9. A = Q⁺ (множество положительных рациональных чисел); B = R (множество действительных чисел); "xÎA F(x) = .

10. M = Z (множество целых чисел). Бинарное отношение r задано по правилу: a r b Û a² + b² = 19.