Пусть имеется непустое множество V (V ¹ Æ) и пусть V2 - его декартов квадрат, тогда орграфом называется пара множеств G = (V, A), где A Í V2.
Элементы множества V называются вершинами, элементы множества A- дугами орграфа.
 |
Дуга (u,v) - это упорядоченная пара вершин u и v, где u - начало дуги, v - конец дуги:
Матричные способы задания орграфа.
Пусть задан орграф G = (V, A), |V| = p, |A| = q.
1. Матрица смежности (непосредственной достижимости):
A = ||aij||, i,j = 
, где
Матрица не является симметричной.
2. Матрица инцидентности:
B = ||bij||, i = , j = 
, где
Неориентированный граф, полученный из орграфа G в результате снятия ориентации дуг орграфа, называется основанием орграфа.
 |
Обратный граф
- это граф, заданный на том же множестве вершин, у которого все дуги переориентированы, т. е.: $(i,j)ÎA 
(j, i) Î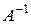 
.
Пример:
Орграф G1 называется симметричным, если для любой дуги (i,j)ÎA существует дуга (j,i)ÎA.
Турниром называется орграф, основание которого - полный граф.
Полустепень исхода вершины v орграфа G есть число дуг, исходящих из этой вершины:
deg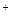 
v = 
v = |{(u, v)|, v, u Î V, (v, u) Î A}|.
Полустепень захода вершины v орграфа G есть число дуг, входящих в данную вершину.
deg 
v = 
v = |{u, v)|v, u Î V, (u, v) Î A}|.
Степенью вершины v орграфа G называется:
deg v = 
v + 
v.
Аналог леммы о рукопожатии для орграфа: сумма полустепеней исхода всех вершины орграфа G равна сумме полустепеней захода всех его вершин и равна числу дуг орграфа G:
.
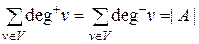МАРШРУТЫ И СВЯЗНОСТЬ
 |
Ориентированным маршрутом называется конечная чередующаяся последовательность вершин и дуг орграфа G такая, что каждая дуга исходит из предыдущей вершины маршрута и заходит в последующую:
Обозначается: M = (v0, а1, v1, а2, …, аn, vn), где ai = (vi – 1, vi), i,j =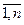 
.
Цепь - это ориентированный маршрут без повторяющихся дуг.
Путь - это цепь без повторяющихся вершин (аналог простой цепи для неорграфа).
Циклический маршрут – этозамкнутая цепь.
Контур - это замкнутый путь.
Длина маршрута - количество дуг, образующих данный маршрут, причем каждая дуга считается столько раз, сколько раз она входит в маршрут.
Если существует (u, v)-маршрут, то вершина v - достижима из вершины u, и вершина u контрдостижима для вершины v, если существует (v, u)-маршрут.
Если вершины u и v достижимы друг для друга, то они называются взаимодостижимыми.
Полумаршрутом в орграфе G называется маршрут его основания:
 |
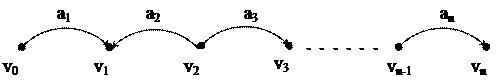аi = (vi – 1, vi), или аi = (vi, vi – 1) i,j = .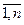
ТИПЫ СВЯЗНОСТИ ОРГРАФА
Орграф называется сильным (сильно связанным), если любые две его вершины достижимы друг для друга.
Орграф называется односторонним (односторонне связанным), если для каждой пары его вершин, по крайней мере, одна достижима из другой.
Орграф называется слабым (слабо связанным), если любые две его вершины соединены полумаршрутом.
Пример:
Орграф называется несвязным, если его основание не связно.
Замечание. Определения подграфов и порожденных подграфов для ориентированных графов аналогичны соответствующим определениям для графов неориентированных.
