Длиной маршрута ( v0,v1, …, vn) называется число ребер, содержащихся в маршруте, причем каждое ребро учитывается столько раз, сколько оно встречается в маршруте.
Пример:
Длина маршрута M=(v0,v1, …, vn) равна n.
Любому ребру приписывается единичная длина, если граф не является взвешенным.
Взвешенным (нагруженным) называется граф, у которого каждому ребру поставлено в соответствии некоторое число, называемое весом или длиной ребра.
Достаточно задать матрицу весов:
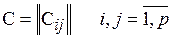 , где
, где
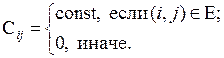
Обхватом графа Gназывается длина наименьшего простого цикла графа G, если таковой имеется; обозначается: g(G).
 |
Окружением графа Gназывается длина наибольшего простого цикла графа G, если таковой имеется; обозначается: C(G).
Пример:
Расстоянием между двумя вершинами u и vграфа G называется длина кратчайшей простой цепи, соединяющей эти вершины; обозначается: d(u,v).
Если вершины u и vграфа G не связаны, расстояние считается равным бесконечности: d(u,v)=¥.
В связном графе расстояние является метрикой, т.е. удовлетворяет следующим аксиомам.
" u,v,w ÎV:
1) d(u,v)³0 (d(u,v)=0 <=> u=v);
2) d(u,v)=d(v,u);
3) d(u,v)+d(v,w)= d(u,w).
Кратчайшая простая цепь, соединяющая вершины u и v, называется геодезической и обозначается: s(u,v).
Алгоритм нахождения кратчайших маршрутов (волновой).
Пусть задан неориентированный граф G=(V,E). Необходимо найти расстояние от одной заданной вершины до другой, или от одной заданной ко всем остальным вершинам графа G.
Идея алгоритма:
– выбирается некоторая вершина графа G и определяются все “соседи” выбранной вершины (“соседями” называются вершины, смежные с данной);
– эти вершины помечаются;
– определяются “соседи соседей” и также помечаются и т. д.
Алгоритм заканчивает работу, если:
– все вершины помечены (граф связен);
– построены все геодезические, связывающие данную вершину со всеми остальными;
– найдены расстояния от данной вершины ко всем остальным.
Если не все вершины в результате работы алгоритма помечены, это означает что граф G не связен.
Пример:
| v1 | v2 | v4 | v6 | v3 | v5 | v9 | v10 | v7 | v8 |

Эксцентриситетом, или отклоненностью, вершины v графа G называется длина максимальной геодезической, исходящей из этой вершины; обозначается: 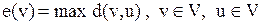 .
.
Диаметром графа G называется максимальный среди всех эксцентриситетов вершин графа; обозначается:  .
.
Периферией графа G называется множество вершин графа G, для которых эксцентриситет равен диаметру, т.е.: 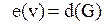 .
.
Радиусом графа G называется минимальный из эксцентриситетов вершин графа G; обозначается: r(G)=min e(u), uÎV.
Центром графа G называется множество вершин, для которых эксцентриситет равен радиусу графа. т.е.: e(v) = r(G).
Примеры:
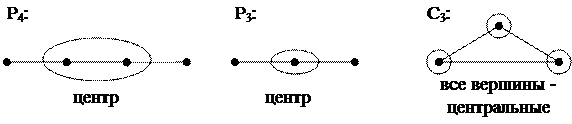
Определим матрицу расстояний:
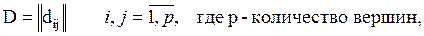
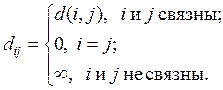
Матрица расстояний несвязного графа может состоять из нескольких матриц (для каждой компоненты) или иметь блочный вид.
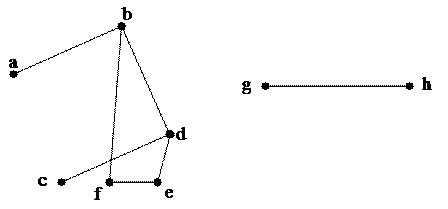 |
Пример: найти e(v) в заданном графе
Используем волновой алгоритм.
Первая компонента связности графа G:
| v | j | u | 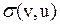
| d(u,v) |
| a | a | a | ||
| b | ab | |||
| d | abd | |||
| f | abf | |||
| c | abdc | |||
| e | abfe |
Вторая компонента связности графа G:
| v | j | u | 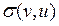
| d(u,v) |
| g | g | g | ||
| h | gh |
Построим матрицу расстояний:

d(G)=3; r(G)=2; периферия: {a,c,e,f}; центр: {b,d} - для первой компоненты связности.
d(G)=1; r(G)=1; периферия: {g,h}; центр: {g,h} - для первой компоненты связности.






