Вершинная и реберная связность

 

Вершинной связностью графа G называется наименьшее число вершин, удаление которых приводит к несвязному, или тривиальному, графу; обозначается: c(G).

c(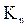)=n-1; c()=1; c()=2.

Реберной связностью графа G называется наименьшее число ребер, удаление которых приводит к несвязному графу; обозначается: .

l(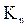)=n-1; l()=1; l()=2.

 

Для тривиального графа реберную связность полагают равной 0.

Пример:

 

Вершина v графа G называется точкой сочленения, или разделяющей вершиной, если граф G\{v} имеет больше компонент связности, чем граф G.

Ребро е графа G называется мостом, если его удаление приводит к нарушению связности графа.

Пример:

 

Связный непустой граф называется неразделимым, если в нем отсутствуют точки сочленения.

Блок – это максимальный неразделимый подграф исходного графа.

Теорема Уитни. Пусть - минимальная степень вершин графа G, тогда справедливо следующее неравенство: c(G) .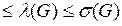

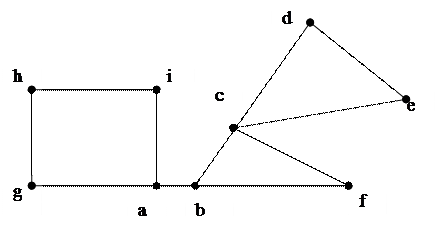Пример:

 

 

Граф не является неразделимым;

блоки графа: {c,d,e},{c,b,f},{a,g,h,i},{a,b}.

 

 

КРАТЧАЙШИЕ МАРШРУТЫ В ГРАФАХ

 

Пусть задан граф G=(V,E), ребрам которого приписаны веса (стоимости), задаваемые матрицей 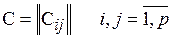. Задача состоит в нахождении кратчайшего пути от заданной начальной вершины s Î V до заданной конечной вершины t Î V при условии, что такой путь существует. Элементы матрицы весов могут быть положительными, отрицательными или нулевыми. Единственное ограничение состоит в том, чтобы граф не содержал циклов с суммарным отрицательным весом.

Задачи данного типа имеют следующие модификации:

- для заданной начальной вершины s найти кратчайшие пути от нее ко всем другим вершинам графа;

- найти кратчайшие пути между всеми парами вершин графа.

 

 

АЛГОРИТМ ДЕЙКСТРЫ

 

Постановка задачи. Имеется произвольный взвешенный (n,m)-граф (в матрице весов нет отрицательных чисел), т.е.:

Требуется найти кратчайший маршрут от вершины s ко всем остальным вершинам графа.

Алгоритм основан на приписывании вершинам временных пометок, причем пометка вершины дает верхнюю границу длины пути от s к данной вершине. Эти пометки постепенно уменьшаются с помощью итерационной процедуры, и на каждом шаге итерации одна из временных пометок становится постоянной. Последнее указывает на то, что пометка уже не является верхней границей, а дает точную длину кратчайшего пути от s к рассматриваемой вершине.

Алгоритм.

Пусть l(x_i) – пометка вершины x_i, Г(р) – множество вершин графа, смежных с вершиной р.

Шаг 1. Присвоение начальных значений.

Положить l(s)=0 и считать эту пометку постоянной. Положить l(x_i)=¥ для всех x_i ≠s и считать эти пометки временными. Положить p=s.

Шаг 2. Обновление пометок.

Для всех x_i ÎГ(р), пометки которых временные, заменить пометки в соответствии со следующим выражением:

l(x_i)=min[l(x_i),l(p)+c(p,x_i)]. (1)

Шаг 3. Превращение пометки в постоянную.

Среди всех вершин с временными пометками найти такую, для которой

l(x_i^*)=min[l(x_i)].

Шаг 4. Считать пометку вершины x_i^* постоянной; положить р= x_i^*.

Шаг 5. Если р=t, то l(p) является длиной кратчайшего пути. Останов.

Если р¹t, то перейти к шагу 2.

 

Замечание. Как только длины кратчайших путей будут найдены, сами пути можно получить при помощи рекурсивной процедуры с использованием соотношения

L(x_i’)+c(x_i’, x_i)=L(x_i);

т.к. вершина x_i’ непосредственно предшествует вершине x_i в кратчайшем пути от s к x_i, то для любой вершины x_i соответствующую вершину x_i’ можно найти как одну из оставшихся вершин.

 

Пример:

 

 

Матрица весов для графа G:

		∞		∞
	∞		∞		∞
		∞
	∞					∞	∞
		∞
				∞
				∞

 

Найти кратчайшие расстояния от 1 вершины ко всем остальным.

1) l(1) = 0;

l(2) = l(3) = … = l(7) =∞;

p = 1.

2) Г(1) = {3,5,6,7};

l(3) = min(l(3), l(1)+C(1,3)) = min(∞,0+4)=4;

l(5) = min(l(5), l(1)+C(1,5)) = 16;

l(6) = min(l(2), l(1)+C(1,2)) = 14;

l(7) = min(l(2), l(1)+C(1,2)) = 2.

3) min(4,16,14,2) = 2;

min = l(7) = 2;

p = 7.

4) Г(7) ={1,2,3,5,6};

l(2) = min(l(2), l(7)+C(2,7)) = min(∞, 2+9)=11;

l(3) = min(l(3), l(7)+C(3,7)) = 4;

l(5) = min(l(5), l(7)+C(5,7)) =16;

l(6) = min(l(6), l(7)+C(6,7)) = 14.

5) min(11,4,16,14) = 4;

min = l(3) = 4;

p = 3.

6) Г(3) = {1,4,5,6,7};

l(4) = min(l(4), l(3)+C(4,3)) = 13;

l(5) = min(l(5), l(3)+C(5,3)) = 16;

l(6) = min(l(6), l(3)+C(6,3)) = 14.

7) min(13,16, 14) = 13;

min = l(4) = 13;

p=4.

8) Г(4) = {2,3,5};

l(5) = min(l(5), l(4)+C(5,4)) = 16;

l(2) = min(l(6), l(3)+C(6,3)) = 11.

9) min(11,16) = 11;

min = l(2) =11;

p = 2.

10) Г(2) = {4,6,7};

l(6) = min(l(6), l(2)+C(2,6)) = 14.

11) min = l(6) =14;

p = 6.

12) l(5) = min(l(5), l(6)+C(5,6)) = 16;

p=5.

 

Таким образом, найдены следующие кратчайшие маршруты от вершины 1:

(1-2): (1,7,2)=11;

(1-3): (1,3)=4;

(1-4): (1,3,4)=(1,7,3,4)=(1,7,2,4)=13;

(1-5): (1,5)=16;

(1-6): (1,6)=14;

(1-7): (1,7)=2.

 

 

АЛГОРИТМ ФОРДА

 

Алгоритм Форда – обобщение алгоритма Дейкстры для случая, когда некоторые ребра имеют отрицательные веса.

На шаге 2 алгоритма пересчет l(x) с помощью соотношения (1) производится для любых вершин, а не только для непомеченных. Значения l(x) могут уменьшаться как для помеченных, так и для непомеченных вершин, т.к. существуют ребра с отрицательным весом.

Если для некоторой помеченной вершины х происходит уменьшение величины l(x), то с этой вершины пометка снимается.

Процедура заканчивается, когда все вершины помечены, и после выполнения шага 2 ни одна из величин l(x) не изменяется.

 

Алгоритм.

Пусть l^k(x_i) – пометка вершины х_i в конце (k+1)-й итерации, Г(s) – множество вершин, смежных с вершиной s.

Шаг 1. Присвоение начальных значений.

Положить S= Г(s), k=1, l¹(s)=0, l¹(x_i)=c(s, x_i) для всех x_iÎ Г(s). Положить l¹(x_i)=¥ для всех остальных x_i.

Шаг 2. Обновление пометок.

Для каждой вершины x_i Î Г(s) (x_i¹s) изменить ее пометку следующим образом:

l^k+1(x_i)=min[l^k(x_i),min{ l^k(x_i)+c(x_j, x_i)}] для x_jÎ T_i, где T_i=Г(x_i)ÇS.

Шаг 3. Проверка на окончание.

Если k£n-1 и l^k+1(x_i)= l^k(x_i) для всех x_i, то пометки равны длинам кратчайших путей. Останов.

Если k<n-1 и l^k+1(x_i)¹ l^k(x_i) для некоторой вершины x_i, то перейти к шагу 4.

Если k=n-1 и l^k+1(x_i)¹ l^k(x_i) для некоторой вершины x_i, то в графе существует цикл отрицательного веса и задача не имеет решения. Останов.

Шаг 4. Подготовка к следующей итерации.

Обновить множество следующим образом:

S={x_i | l^k+1(x_i) ¹ l^k(x_i)}.

Шаг 5. Положить k=k+1 и перейти к шагу 2.

Замечание. Алгоритм Форда не решает задачу при наличии цикла отрицательной длины. Для его обнаружения в процессе работы алгоритма просчитывается, сколько раз помечается каждая вершина: если вершина помечается ровно n раз, где n – число вершин графа, - процедура заканчивает работу: существует цикл отрицательной длины.

Пример:

 

Матрица весов для графа G:

		∞		∞
	∞		∞		∞
		∞
	∞					∞	∞
		∞
				∞
				∞

 

 

1) s=1; вершины, смежные вершине 1: S= Г(s)={3,5,6,7},

k=1; l¹(1)=0,

l¹(3)=4, l¹(5)=16, l¹(6)=14, l¹(7)=2, l¹(2)= l¹(4)=¥;

2) Г(s)={2,3,4,5,6,7} - вершины, смежные вершинам 3,5,6,7;

для 2: Т₂={7,6,4}Ç{3,5,6,7}={7,6}, где {7,6,4} - вершины, смежные вершине 2;

l²(2)=min(¥, min(2+9,14+3))=11;

для 3: Т₃={1,4,5,6,7}Ç{3,5,6,7}={5,6,7}, где {1,4,5,6,7} - вершины, смежные вершине 3;

l²(3)=min(4, min(16+12,14+10,2+2))=4;

для 4: Т₄={2,3,5}Ç{3,5,6,7}={3,5}, где {2,3,5} - вершины, смежные вершине 4;

l²(4)=13;

для 5: Т₅={1,3,4,6,7}Ç{3,5,6,7}={3,6,7}, где {1,3,4,6,7} - вершины, смежные вершине 5;

l²(5)= 16;

для 6: Т₂={1,2,3,5,7}Ç{3,5,6,7}={3,5,7}, где {1,2,3,5,7} - вершины, смежные вершине 6;

l²(6)= 14;

для 7: Т₂={1,2,3,5,6}Ç{3,5,6,7}={3,5,6}, где {1,2,3,5,6} - вершины, смежные вершине 7;

l²(7)=2;

3) переходим к шагу 4, обновляем множество S;

4) S={2,4};

5) k=2; переходим к шагу 2;

6) Г(S)={2,3,4,5,6,7} - вершины, смежные вершинам 2,4;

для 2: Т₂={7,6,4}Ç{2,4}={4};

l³(2)=min(11, 13+2))=11;

для 3: Т₃={1,4,5,6,7}Ç{2,4}={4};

l³(3)=min(4, 13+9)=4;

для 4: Т₄={2,3,5}Ç{2,4}={2};

l³(4)= min(13, 11+2)=13;

для 5: Т₅={1,3,4,6,7}Ç{2,4}={4};

l³(5)= 16;

для 6: Т₂={1,2,3,5,7}Ç{2,4}={2};

l³(6)= 14;

для 7: Т₂={1,2,3,5,6}Ç{2,4}={2}

l³(7)=2.

7) k£n-1 и l^k+1(x_i)= l^k(x_i) для всех x_i, следовательно, пометки равны длинам кратчайших путей.

 

Кратчайшие маршруты от вершины 1:

(1-2):(1,7,2)=11;

(1-3): (1,3)=4;

(1-4): (1,3,4)=(1,7,3,4)=(1,7,2,4)=13;

(1-5): (1,5)=16;

(1-6): (1,6)=14;

(1-7): (1,7)=2.

 

АЛГОРИТМ ФлойДА

Алгоритм базируется на использовании последовательности из n преобразований (итераций) начальной матрицы весов. При этом на k-той итерации матрица представляет длины кратчайших путей между каждой парой вершин с тем ограничением, что путь между x_i и x_j (для любых x_i и x_j) содержит в качестве промежуточных только вершины из множества { x₁, x₂,…, x_n}.

Все циклы в графе G имеют неотрицательный суммарный вес.

 

Алгоритм.

Шаг 1. Присвоение начальных значений.

Положить k=0.

Шаг 2.

k=k+1.

Шаг 3.

Для всех i ¹ k таких что c_ik¹¥, и для всех j ¹k таких что c_kj ¹¥ введем операцию:

c_ij=min[c_ij, (c_ik+c_kj)]. (2)

Шаг 4. Проверка на окончание.

Если c_ij <0, то в графе существует цикл отрицательного веса, содержащий вершину x_i; решения нет. Останов.

Если все c_ij ³ 0 и k=n, то получено решение и матрица дает длины всех кратчайших путей. Останов.

Если все c_ij ³ 0, но k<n, то вернуться к шагу 2.

 

Пример:

 

Пусть задан граф G следующего вида:

 

 

Матрица весов: Матрица путей:

k=0;

k=1;

		∞		∞
	∞		∞		∞
		∞
	∞					∞	∞
		∞
				∞
				∞

 

 

k=2;

		∞		∞
	∞		∞		∞
		∞
	∞
		∞

 

 

k=3;

		∞
	∞		∞		∞
		∞
		∞

 

k=4;

 

 

 

k=5;

 

 

k=6;

 

 

k=7;

 

 

Матрица q=[q_ij] – матрица, в которой элемент q_ij указывает вершину, непосредственно предшествующую вершине х_j в кратчайшем пути от х_i к х_j. Матрице q присваиваются начальные значения q_ij= х_i для всех х_i и х_j. На шаге 3 алгоритма обновление матрицы происходит следующим образом:

 

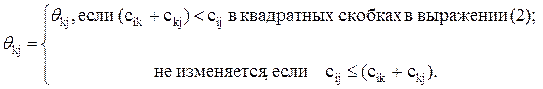
В конце алгоритма кратчайшие пути получаются непосредственно из заключительной матрицы q.

 

Таким образом, матрица всех кратчайших маршрутов:

 

 

Матрица путей:

 

		1,7,2	1,3	1,3,4	1,5	1,6	1,7
	2,7,1		2,4,3	2,4	2,4,5	2,6	2,7
	3,1	3,4,2		3,4	3,5	3,6	3,7
	4,3,1	4,2	4,3		4,5	4,2,6	4,2,7
	5,1	5,4,2	5,3	5,4		5,6	5,7
	6,1	6,2	6,3	6,2,4	6,5		6,7
	7,1	7,2	7,3	7,2,4	7,5	7,6

 

Кратчайшие маршруты от вершины 1:

 

 

(1-2): (1,7,2)=11;

 

(1-3): (1,3)=4;

 

 

(1-4): (1,3,4)=(1,7,3,4)=(1,7,2,4)=13;

(1-5): (1,5)=16;

 

(1-6): (1,6)=14;

 

(1-7): (1,7)=2.

 

Контрольные вопросы

 

1. Определение маршрута, цепи, цикла.

2. Какой граф называется связным? Что такое компонента связности?

3. Привести примеры графов, которые имеют все периферийные и все центральные вершины.

4. Что такое эксцентриситет?

5. Чем диаметр графа отличается от его радиуса (дайте их определение)?

6. Что такое число вершинной и реберной связности?

7. Дайте определения моста и точки сочленения.

8. Для произвольного графа постройте матрицу расстояний (вес любого ребра равен 1).

9. Привести пример графа, удовлетворяющего строгому неравенству теоремы Уитни.

10. Сформулируйте задачу нахождения кратчайших маршрутов в графе.

 

ДЕРЕВЬЯ И ОСТОВЫ