Пример выполнения курсового проекта

Задание. Провести проектирование, структурное, кинематическое, силовое и динамическое исследования механизмов двухцилиндрового четырехтактного двигателя (рис 1)

Рис. 1. Схема механизмов четырехтактного двигателя внутреннего сгорания

Таблица - Исходные данные для проектирования и исследования

Наименование параметров	Обозначение параметра	Величина	Обозначение единиц измерения

Угловая скорость вращения кривошипа ОА	ω₁		рад/сек
Отношение длины шатуна к длине кривошипа	λ	3,5
Максимальное индикаторное давление	p		МПа
Диаметры цилиндров	D₃=D₅	0,12	м
Массы шатунов 2 и 4	m₂=m₄	2,5	кг
Массы поршней 3 и 5	m₃=m₅		кг

Продолжение таблицы


Моменты инерции шатунов 2 и 4	I_S2=I_S4	0,011	кг м
Коэффициент неравномерности движения	δ	0,05

Угол развала осей γ=90°, центры масс шатунов S₂ и S₄ находятся из условия AS₂=AS₄=0,28l_AB. На тактах всасывания и выхлопа давление в цилиндрах можно принять равным атмосферному

СИНТЕЗ, СТРУКТУРНОЕ И КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ РЫЧАЖНОГО МЕХАНИЗМА ДВИГАТЕЛЯ

Проектирование кривошипно-ползунного механизма

Используя формулы и исходные данные определяем длины кривошипа ОА, шатуна АВ

Структурное исследование рычажного механизма

Определяем степень подвижности механизма по формуле П. Л. Чебышева.

где п = 5 — число подвижных звеньев;

р₅=7 — число кинематических пар пятого класса, 1 рода;

р₄ = 0 — число кинематических пар четвертого класса, 2 рода.

Подставим эти данные в формулу Чебышева и находим:

Определяем класс и порядок механизма. Для этого расчленим механизм на группы Ассура. Он состоит из двух групп Ассура II класса, 2-го вида, 2-го порядка (рис. 2) и меха-

Рис.2- Группы Ассура

низма I класса, состоящего из входного звена 1 и стойки 6. В целом рассматриваемый механизм II класса.

Построение схемы механизма

Масштаб схемы. Приняв на чертеже (см. лист 1 приложения) отрезок ОА = 30 мм, находим:

В принятом масштабе вычерчиваем схему механизма. Для построения 12 положений звеньев механизма разделим траекторию, описываемую точкой А кривошипа ОА, на 12 равных частей. За нулевое принимаем то положение кривошипа ОА, при котором точка В левого поршня занимает крайнее нижнее положение. Из отмеченных на окружности точек А_o_, А₁…А₁₁ раствором циркуля, равным АВ=АС= мм

намечаем на линии движения ползуна 3 точки Во, В₁, В₂…В11, а на линия движения ползуна 5 точки Со, С₁, С₂... С₁₁. Соединяем прямыми точки Ао с Во и Со, А₁ с B₁ и С₁ и т.д., получаем 12 положений звеньев механизма.

Построение планов скоростей механизма

Построение начинаем от входного звена, т. е. кривошипа ОА. Из точки р, принятой за полюс плана скоростей (лист 1 приложения), откладываем в направлении вращения кривошипа ОА вектор скорости точки А: ра=41,4 мм.

Построение плана скоростей группы Ассура II класса 2-го вида (звенья 2 и 3) производим по уравнению:

где V_А— скорость точки А кривошипа ОА. Ее величина равна

ω- угловая скорость кривошипа

V_ВА — скорость точки В звена 2 во вращательном движении относительно точки А направлена перпендикулярно оси звена АВ;

V_В — скорость точки В ползуна 3, направлена вдоль оси ОВ, параллельно направляющей.

Из точки а проводим линию, перпендикулярную оси звена АВ, а из полюса р плана скоростей—линию, параллельную оси ОВ. Точка b пересечения этих линий дает конец вектора искомой скорости V_В

Построение планов скоростей для другой группы Ассура II класса 2-го вида (звенья 4 и 5) производится согласно уравнению

где V_СА — скорость точки С звена 4 во вращательном движении относительно точки А, направлена перпендикулярно оси звена АС;

Vc—скорость точки С ползуна 5 направлена вдоль оси ОС.

Масштаб планов скоростей вычисляем по формуле

Скорости точек S₂ и S₄ определяем по правилу подобия. Так как , то и отрезки as₂ и as₄ на плане скоростей будут равны: as2=0,28ab, as4=0,28ac. Найденные точки S₂ и S₄ соединяем с полюсом р. Истинное значение скорости каждой точки находим по формулам:

, , ,

Полученные значения сводим в таблицу 1.

Таблица 1 - Значения скоростей точек кривошипно-ползунного механизма в м/с

Определяем угловые скорости шатунов АВ и АС для 12 положений и сводим полученные значения в таблице 2.

Таблица 2 - Значения угловых скоростей шатунов АВ и АС в рад/с

Направление угловой скорости звена АВ определяем следующим образом. Переносим (мысленно) вектор ab с плана скоростей в точку В шатуна ВА кривошипно-ползунного механизма и наблюдаем направление поворота звена АВ вокруг точки А. Аналогично определяется угловая скорость и другого шатуна. Так, например, в 10-м положении звено АВ вращается по часовой стрелке(знак «-»), а звено АС — против (знак «+»).

Построение планов ускорений механизма

Построение плана ускорений рассмотрим для 10-го положения механизма (лист 1, вкладка 1). Так как кривошип ОА вращается с постоянной угловой скоростью ω=138 рад/с, то точка А звена ОА будет иметь только нормальное ускорение, величина которого равна

Определяем масштаб плана ускорений.

где πа=38,1 мм — длина отрезка, изображающего на плане ускорений вектор нормального ускорения точки А кривошипа ОА.

Из произвольной точки π — полюса плана ускорений проводим вектор πа параллельно звену ОА от точки А к точке О. Построение плана ускорений группы Ассура II класса 2-го вида (звенья 2, 3) проводим согласно уравнению

где — ускорение ползуна 3, направлено вдоль оси ОВ, параллельно направляющей,

—нормальное ускорение точки В шатуна АВ при вращении его вокруг точки А, направлено вдоль оси звена АВ от точки В₁₀ к точке А₁₀.

Его масштабная величина, обозначим ее через an_ba, равна

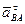— касательное ускорение точки В шатуна АВ при вращении его вокруг точки А (величина неизвестна) направлено перпендикулярно к оси звена АВ.

Из точки а вектора πа плана ускорений проводим прямую, параллельную оси звена ВА, и откладываем на ней в направлении от точки В₁₀ к точке А₁₀ отрезок an_ba=3 мм. Через конец вектора an_BA проводим прямую, перпендикулярную к оси звена ВА произвольной длины Из полюса π проводим прямую, параллельную оси ОВ. Точка b пересечении этих прямых определит концы векторов πb и . Складывая векторы n_ba и , получаем полное ускорение звена АВ, для этого соединяем точки а и b прямой. Точку s₂ на плане ускорений находим по правилу подобия, пользуясь соотношением отрезков Так как AS₂=0,28AB, то и as₂=0,28ab= 0,28*33=92 мм. Соединяем точку s₂ с полюсом π.

Аналогично проводим построение для шатуна АС и ползуна 5, пользуясь следующим векторным уравнением:

где а_c — ускорение ползуна 5, направлено вдоль оси ОС;

— нормальное ускорение точки С шатуна АС при вращении его вокруг точки А, направлено вдоль оси звена АС от точки С₁₀ к точке А₁₀.

Его масштабная величина an_СА равна

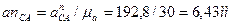
— касательное ускорение точки С шатуна СА при вращении его вокруг точки А (величина его неизвестна) направлено перпендикулярно к оси звена АС.

Из точки а вектора πа плана ускорений проводим прямую, параллельную оси звена СА, и откладываем на ней в направлении от точки С₁₀ к А₁₀ отрезок 6,5 мм. Через конец вектора a проводим прямую, перпендикулярную к оси звена АС, произвольной длины. Из полюса π проводим прямую, параллельную оси ОС Точка с пересечения этих прямых определит концы векторов и Вектор πs₄ ускорения точки S₄ шатуна АС определяем аналогично вектору πs₂.

Численные значения ускорений точек В, С, S₂, S₄, а также касательные ускорения 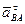и найдем по формулам:

Определяем величины угловых ускорений звеньев АВ и АС:

Определяем направление углового ускорения звена АВ. Для этого мысленно переносим вектор в точку B₁₀. Считая точку А₁₀ неподвижной, замечаем, что поворот звена АВ будет по часовой стрелке (знак «-»). Для звена АС переносим вектор в точку С₁₀. Видим, что угловое ускорение направлено также по часовой стрелке (знак «-»). Два других плана ускорений строятся аналогично