Пример расчета неразветвленной электрической цепи переменного тока.

Задача. Конденсатор емкостью С =3,4 мкФ и катушка с активным сопротивлением

R = 50 Ом и индуктивностью L = 29,8 мГн подключены последовательно к

генератору переменного тока с напряжением U = 200 В и частотой ƒ = 250 Гц.

Определить ток, активную, реактивную и полную мощности катушки, конденсатора и всей цепи при неизменном напряжении генератора и условиях: X_L > X_C (ƒ > ƒ_P), X_L< X_C (ƒ < ƒ_P), X_L = X_C (ƒ = ƒ_P).

 

Дано: R = 50 Ом L = 29,8 мГн С =3,4 мкФ U = 200 В ƒ = 250 Гц

Определить: X_L, X_C, Z, I, P, Q_L, Q_C, Q.

Решение

Электрическая схема

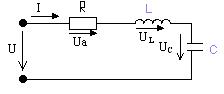
Для решения задачи определяем резонансную частоту контура: 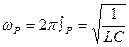, откуда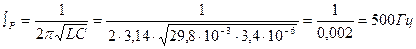

 

Расчет цепи при условии X_L > X_C; ƒ > ƒ_P, принимаем ƒ = 600 Гц

1. Определяем реактивные и полное сопротивление цепи:

X_L = 2πƒL =6,28 ∙ 600 ∙ 29,8∙10^-3 =112,3 Ом

X_с = 1/ 2πƒC = 1 / 6,28 ∙ 600 ∙ 3,4∙10^-6 = 78 Ом

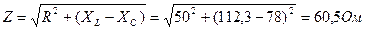
2. Определяем ток в цепи: I = U / Z = 200 / 60,5 = 3,3 A.

3. Определяем угол сдвига фаз между током и напряжением из треугольника сопротивлений:

cos φ = R / Z = 50 / 60,5 = 0,8264; sin φ = X_L − X_C / Z = 112,3 – 78 / 60,5 = 0,566

4. Определяем активную мощность:

Р = U I cos φ = 200∙3,3∙0,8264 = 545,4 Вт

5. Определяем реактивные мощности катушки и конденсатора:

Q_L = I² X_L =3,3²∙112,3 =1222,95 вар; Q_С = I² X_С =3,3² ∙ 78 =849,42 вар

6. Определяем реактивную мощность цепи:

Q = Q_L - Q_С = 1222,95 – 849,42 = 373,5 вар или Q = U I sin φ = 200∙3,3∙0,566 = 373,5 вар

7. Определяем полную мощность цепи: S = UI = 200 ∙ 3,3 = 660 BA

 

Расчет цепи при условии X_С > X_L; ƒ < ƒ_P, принимаем ƒ = 250 Гц

1. Определяем реактивные и полное сопротивление цепи:

X_L = 2πƒL =6,28 ∙ 250 ∙ 29,8∙10^-3 = 46,8 Ом

X_с = 1/ 2πƒC = 1 / 6,28 ∙ 250 ∙ 3,4∙10^-6 = 187 Ом

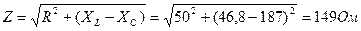
2. Определяем ток в цепи: I = U / Z = 200 / 149 = 1,34 A.

3. Определяем угол сдвига фаз между током и напряжением из треугольника сопротивлений:

cos φ = R / Z = 50 / 149 = 0,335; sin φ = X_L − X_C / Z = 46,8 – 187 / 149 = − 0,94

4. Определяем активную мощность:

Р = U I cos φ = 200∙1,34 ∙0,335 = 90 Вт

5. Определяем реактивные мощности катушки и конденсатора:

Q_L = I² X_L =1,34²∙46,8 = 84 вар; Q_С = I² X_С =1,34² ∙ 187 = 336 вар

6. Определяем реактивную мощность цепи:

Q = Q_L - Q_С = 84 – 336 = − 252 вар или Q = U I sin φ = 200∙3,3∙0,566 = 373,5 вар

7. Определяем полную мощность цепи: S = UI = 200 ∙ 1,34 = 268 BA

 

Расчет цепи при условии X_L = X_C; ƒ = ƒ_P, принимаем ƒ = 500 Гц

1. Определяем реактивные и полное сопротивление цепи:

X_L = 2πƒL =6,28 ∙ 500 ∙ 29,8∙10^-3 = 93,6 Ом

X_с = 1/ 2πƒC = 1 / 6,28 ∙ 500 ∙ 3,4∙10^-6 = 93,6 Ом

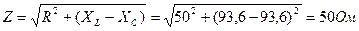, т.е. Z = R = 50 Ом

2. Определяем ток в цепи: I = U / Z = 200 / 50 = 4 A.

3. Определяем угол сдвига фаз между током и напряжением из треугольника сопротивлений:

cos φ = R / Z = 50 / 50 = 1; sin φ = X_L − X_C / Z = 93,6 – 93,6 / 50 = 0

4. Определяем активную мощность:

Р = U I cos φ = 200∙ 4 ∙ 1 = 800 Вт

5. Определяем реактивные мощности катушки и конденсатора:

Q_L = I² X_L =4²∙93,6 = 1497,6 вар; Q_С = I² X_С =4² ∙ 93,6 = 1497,6 вар

6. Определяем реактивную мощность цепи:

Q = Q_L - Q_С = 1497,6 – 1497,6 = 0 вар или Q = U I sin φ = 200∙4∙0 = 0 вар

7. Определяем полную мощность цепи: при резонансе напряжений S = P = 800 ВА

 

Задание для Задачи 4.

Вариант 1

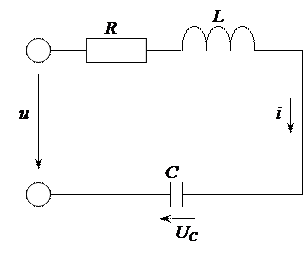
Дано: R =11 Ом; L =9,55 мГн; С =200 мкФ; f =100 Гц; U_C =15 В.

Определить: U; I; P; Q. Построить векторную диаграмму.

 

Вариант 2

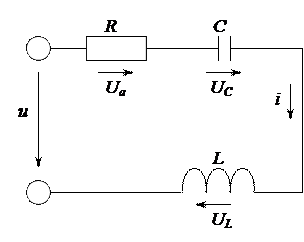
Дано: u = 141 sin 628 t; R =3 Ом; L =0,0191 Гн; С =200 мкФ.

Определить: I; U_a; U_L; U_C; P; Q; S. Построить векторную диаграмму.

 

 

Вариант 3

 

Дано: u = 564 sin ωt; R ₁=8 Ом; R ₂=8 Ом; L =0,0383 Гн; f =50 Гц.

Определить: I; S; P; Q. Построить векторную диаграмму.

 

Вариант 4

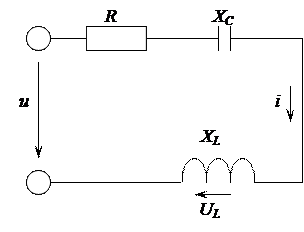
Дано: u = 169 sin 628 t; R =12 Ом; L =9,55 мГн; С =265 мкФ.

Определить: I; Z; U_L; P; Q. Построить векторную диаграмму.

 

Вариант 5

Дано: u = 294 sin 314 t; R =5 Ом; L =19,1 мГн; С =159 мкФ.

Определить: U_L; Р; Q; S. Построить векторную диаграмму.

 

 

Вариант 6

 

Дано: u = 113 sin 628 t; R =2 Ом; L =9,6 мГн; С =266 мкФ.

Определить: I; P; Q; S. Построить векторную диаграмму.

 

 

Вариант 7

 

Дано: R =3 Ом; L =19,1 мГн; С =530 мкФ; f =50 Гц; U_а =20 В.

Определить: U; P; Q; S. Построить векторную диаграмму.

 

Вариант 8

 

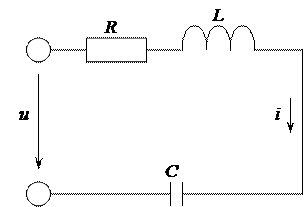
Дано: u = 564 sin 628 t; R =12 Ом; L =19,1 мГн; С =531 мкФ.

Определить: I; P; Q; S. Построить векторную диаграмму.

 

 

Вариант 9

Дано: R =15 Ом; L =6 мГн; С =400 мкФ; f =100 Гц; U_C =20 В.

Определить: U; I; P; Q. Построить векторную диаграмму.

Вариант 10

Дано: u = 180 sin 628 t; R =16 Ом; L =12 мГн; С =260 мкФ.

Определить: I; Z; U_L; P; Q. Построить векторную диаграмму.

ТЕМА: МАГНИТНЫЕ ЦЕПИ.

5. РАСЧЁТ МАГНИТНОЙ ЦЕПИ

Пример расчёта магнитной цепи.

 

 

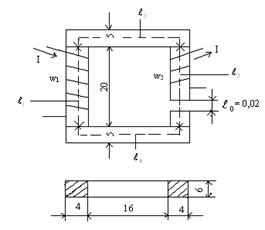
Для магнитной цепи, приведенной на рисунке, заданы линейные размеры в сантиметрах, числа витков обмоток и магнитный поток Ф= 2,4·10^─3 Вб. Оба вертикальных стержня изготовлены из

электротехнической стали 1512(Э42), горизонтальные части – ярма – из литой стали Ст -2. Обе обмотки соединены последовательно и встречно. Определить силу тока в обмотках I для создания

заданного магнитного потока, абсолютную магнитную проницаемость сердечника μ_а1 и

магнитную проницаемость μ₁, где расположена первичная обмотка W₁.

 

Дано: W₁ = 600 W₂ = 200 Ф= 2,4·10^─3 Вб., сталь 1512(Э42), сталь Ст -2.

Определить: I, μ_а1, μ₁

Решение

1. Проводим среднюю магнитную линию и по ней разбиваем цепь на однородные участки

ℓ₁, ℓ₂, ℓ₃, ℓ₄(т.е. одинакового поперечного сечения и магнитной проницаемости).

2. Определяем поперечные сечения сердечника на каждом участке цепи:

S_{1 =} S₂ = 4·6 = 24 см² =24·10^─4 м² S_{3 =} S₄ = 5·6 = 30 см² 30·10^─4 м²

3. Определяем длины каждого участка:

ℓ₁ = ℓ₂ =20 см = 0,2 м ℓ₃ = ℓ₄ = 16+ 2·2 + 2,5·2 = 25 см = 0,25 м.

4. Определяем магнитную индукцию на каждом участке:

В₁ = В₂ = В₀ = Ф/S₁ = 2,4·10^─3/24·10^─4 = 1 Тл

В₃= В₄ = Ф/S₃ = 2,4·10^─3/30·10^─4 = 0,8 Тл

5. По таблице характеристик намагничивания ферромагнитных материалов определяем

напряженность магнитного поля на ферромагнитных участках сердечника:

Н₁ = Н₂ = 185 А/м Н₃ = Н₄ = 682 А/м;

в воздушном зазоре: Н₀ =0,8·10⁶· В_{0 =} 0,8·10⁶·1 = 0,8·10⁶ А/м.

6. По закону полного тока записываем уравнение для определения тока цепи, учитывая встречное

включение обмоток:

I ω₁ ─ I ω₂ = Н₁ℓ₁ + Н₂ℓ₂ + Н₃ℓ₃ + Н₄ℓ₄ + Н₀ℓ₀ или

I(ω₁─ ω₂) = Н₁ℓ₁ + Н₂ℓ₂ + Н₃ℓ₃ + Н₄ℓ₄ + Н₀ℓ₀

400 I = (185·0,2)·2 + (682·0,25)·2 +0,8·10⁶·0,02·10^─2

I = (185·0,2)·2 + (682·0,25)·2 +0,8·10⁶·0,02·10^─2 / 400 =1,436 A

7. Определяем абсолютную магнитную проницаемость сердечника на первом участке цепи:

В₁ = μ_а1· Н₁ μ_а1 = В₁ / Н₁ = 1 / 185 = 0,0054 Гн/м

8. Определяем магнитную проницаемость первого участка магнитной цепи:

μ_а1 = μ₁·μ₀ μ₁ = μ_а1 /μ₀ = 0,0054 / 4π·10^─7 = 0,0054 / 125·10^─8 = 4300

 

Задание для Задачи 5.

Определить силу тока I в обмотках данной цепи для получения заданного магнитного потока Ф, абсолютную магнитную проницаемость μ_{а 1} и магнитную проницаемость μ ₁ участка цепи, где расположена обмотка с числом витков W ₁.

Вариант 1

 

 

Дано: W ₁ = 500; W ₂ = 300; Ф = 1,0·10^–3 Вб; материал сердечника — чугун.

Размеры цепи даны в сантиметрах. Обмотки включены согласно.

Вариант 2

Дано: W ₁ = 100; Ф = 3·10^–3 Вб;

материал сердечника — электротехническая сталь (1211). Размеры цепи даны в сантиметрах.

Вариант 3

Дано: W ₁ = 1200; W ₂ = 600; Ф =1,6·10Вб;

материал сердечника — чугун. Размеры цепи даны в сантиметрах.

Обмотки действуют согласно.

Вариант 4

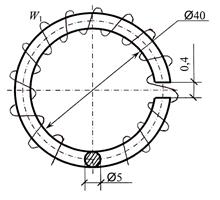Дано: W ₁ = 2000; Ф = 2,8·10^–3 Вб;

материал сердечника — литая сталь (Ст.2). Размеры цепи даны в сантиметрах.

 

Вариант 5

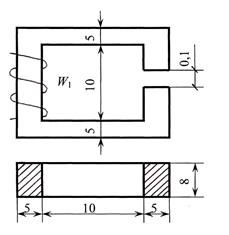Дано: W ₁ = 400; Ф = 4·10^–3 Вб;

материал сердечника — чугун. Размеры цепи даны в сантиметрах.

 

Вариант 6

Дано: W ₁ = 600; W ₂ = 200; Ф = 1,6·10^–3 Вб; материал сердечника — сталь литая (Ст.2). Размеры цепи даны в сантиметрах. Обмотки действуют встречно.

Вариант 7

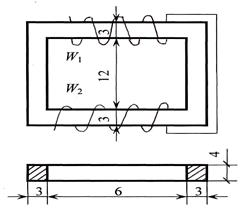Дано: W ₁ = 400; W ₂ = 600; Ф = 1,8·10^–3 Вб;

материал сердечника — электротехническая сталь (Э11) 1211. Размеры цепи даны в сантиметрах. Обмотки действуют согласно.

Вариант 8

Дано: W = 1000; Ф = 0,6·10^–3 Вб; материал сердечника — чугун. Размеры цепи даны в сантиметрах.

Вариант 9

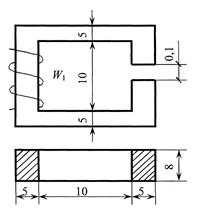Дано: W ₁ = 600; Ф = 8·10^–3 Вб;

материал сердечника — чугун. Размеры цепи даны в сантиметрах.

Вариант 10

Дано: W ₁ = 200; Ф = 6·10^–3 Вб;

материал сердечника — электротехническая сталь (1211). Размеры цепи даны в сантиметрах.

ТЕМА: Основы электроники.

ЗАДАНИЕ 6. ТЕОРЕТИЧЕСКИЙ ВОПРОС.

1. Электропроводность полупроводников. Электронно-дырочный переход. Полупроводниковые диоды.

2. Биполярный транзистор. Полевые транзисторы. Область применения.

3. Тиристоры, светодиоды, фотодиоды. Область применения.

4. Фотоэлектрические приборы. Электронные фотоэлементы с внешним и внутренним фотоэффектом.

5. Электронные выпрямители. Однополупериодный и двухполупериодный выпрямители.

6. Трёхфазный выпрямитель. Стабилизатор напряжения.

7. Электронные усилители. Обратная связь в усилителях.

8. Электронные генераторы. Мультивибратор.

9. Гибридные интегральные микросхемы. Фотолитография.

10. Толстоплёночные и тонкоплёночные микросхемы.