С поверхности металлов теплота передается конвективным путем или посредством радиации. В конечном итоге вся теплота, введенная при сварке, отдается в окружающее пространство и сварное соединение остывает.
При конвективном теплообмене теплота с поверхности уносится жидкостью или газом, которые перемещаются относительно поверхности. Движение жидкости или газа может возникать вследствие различной плотности нагретых или ненагретых зон или в результате принудительной циркуляции жидкости или газа.
Приближенно тепловой поток q2к с единицы поверхности в единицу времени при конвективном теплообмене определяется по правилу Ньютона
,
где aк ¾ коэффициент конвективной теплоотдачи; Т—температура поверхности твердого тела; Тс – температура окружающей среды.
Коэффициент aк может меняться в широких пределах в зависимости от следующих факторов:
от свойств окружающей среды (теплопроводности, плотности, вязкости) и ее движения относительно поверхности;
от физических свойств поверхности, отдающей теплоту;
от формы поверхности тела и ее положения в пространстве;
от разности температур Т-Тс.
При лучистом теплообмене удельный поток излучения определяется по закону Стефана-Больцмана
,
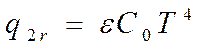где Со = 57,6 нВт/(см2×°К4);
e ¾ коэффициент черноты; для абсолютно черного тела e = 1. Для окисленных шероховатых поверхностей стали e изменяется от 0,6 до 0,95. У алюминия e изменяется от 0,05 до 0,2.
По аналогии с правилом Ньютона для конвективного теплообмена удельный тепловой поток можно связать с разностью температур Т-Тс
q2r = ar (Т-Тс),
где ar – коэффициент лучистого теплообмена.
Тогда удельный поток полной теплоотдачи можно представить как сумму удельных потоков конвективного и лучистого теплообменов:
q2 = ar (T-Tc) +ak (T-Tc) =a (T-Tc),
где a = ar + ak – коэффициент полной теплоотдачи, значительно изменяется с ростом температуры.
При температурах до 400-500 °К основная часть теплоты отдается конвективным теплообменом, при более высоких температурах – лучистым.
Чтобы рассчитать изменение температуры тела, необходимо знание граничных условий:
условия теплообмена;
начальное распределение температуры при t = 0.
Граничное условие 1-ого рода определяет закон изменения температуры точек на поверхности тела. Его частный случай – изотермическое условие, когда температура на поверхности постоянна, что на практике соответствует интенсивному охлаждению поверхности тела проточной жидкостью. В этом случае a = ¥.
Граничное условие 2-ого рода определяет значение теплового потока на границе тела. Практически важным частным случаем является адиабатическая граница, когда отсутствует теплообмен с окружающей средой, т.е. тепловой поток на границе тела равен нулю и a = 0.
Граничное условие 3-его рода определяет теплообмен с окружающей средой по правилу Ньютона
q2S =a(TS-Tc),
где q2S – удельный тепловой поток через границу поверхности S;
Фурье к границе тела по TS – температура тела на поверхности.
По закону ступает теплота 
, при этом q2S = q2.
Из граничного условия 3-его рода могут быть получены изотермическое и адиабатическое условия. Случай a = ¥ соответствует изотермическому, а a = 0 – адиабатическому условию.
