Для визначення корисності використовують поняття лотереї. Для цього експерту пропонують порівняти дві альтернативи:
1) значення показника X;
2) лотерею: отримати Xmin з імовірністю (1 – p) або Xmax з ймовірністю p– L (Xmax; p; Xmin).
Величину ймовірності (p) змінюють поступово до такої величини від 0 до1, доки, на думку експерта, значення показника X і лотерея L (Xmax; p; Xmin) стануть еквівалентними. Тобто всі можливі результати розміщують за зростанням. Корисність найгіршого результату оцінюється як 0, а найкращого – 1 (або як 100): U(Xmin) = 0; U (Xmax) = 100.
Для того щоб оцінити проміжний результат, особі пропонують взяти участь у лотереї. Значення p, за якого особа відмовиться від гарантованого результату на користь участі у лотереї, беруть для розрахунку корисності: U (Xj) = p U (Xmax) + (1 – p) U (Xmin) = 100. Тобто із множини значень відомого показника X експерт повинен розрахувати два: Xmax і Xmin – найбільш пріоритетне і найменш пріоритетне, для яких X не гірше за Xmax, а Xmin не гірше за X.
Корисність варіанту X визначається ймовірністю p – за якої експерту байдуже що обирати: X гарантовано або лотерею L (Xmax; p; Xmin), де Xmax і Xmin – вектори, найбільш і найменш пріоритетні у порівнянні з X.
Для кожної людини буде своє значення ймовірності, за якої їй байдуже, що обирати: гроші гарантовано або участь у лотереї. Ймовірність перетворюють на корисність, помножуючи на100, якщо корисність визначається за 100-бальною шкалою, або помножуючи на10, коли за10-бальною.
Нехай лотерея L приводить до виграшів(подій) X1, X2, …, Xn із відповідними ймовірностями P1, P2, …, Pn і відповідними корисностями U(X1), U(X2), …, U(Xn).
Математичне сподівання виграшу, тобто очікуваний виграш знаходять за формулою:
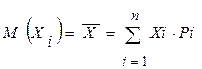
| (4.1) |
Математичне сподівання корисності, тобто очікувану корисність знаходять за формулою:
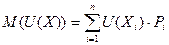
| (4.2) |
Корисність результатів збігається з математичним сподіванням корисності результатів.
Взаємозв’язок ризику із функціями корисності визначається поняттям детермінованого еквіваленту. Детермінований еквівалент лотереї – це гарантована сума Х, отримання якої еквівалентно участі у лотереї і гарантує особі таку саму корисність, як і участь у ризикованій справі, тобто
| U (Х) = M (U(X)) | (4.3) |
Особу, що приймає рішення, називають несхильною до ризику, коли для неї найбільш пріоритетною є можливість одержати гарантовано очікуваний виграш в лотереї, ніж узяти в ній участь.
Із теорії корисності можна зробити висновок, що корисність лотереї збігається з математичним сподіванням корисності її випадкових результатів. Відповідно до цього умова несхильності до ризику набуває такого вигляду:
| U (M(X)) > M(U(X)), | (4.4) |
тобто корисність сподіваного доходу більше сподіваної корисності.
Для функції корисності можна розрахувати премію за ризик в лотереї (π (Х)) як різницю між очікуваним виграшем і детермінованим еквівалентом:
| π (Х) = M(X) – Х | (4.5) |
За своїм фізичним змістом премія за ризик (надбавка за ризик) – це сума в одиницях виміру показника X, якою суб’єкт управління згоден поступитися із середнього виграшу, щоб уникнути ризику, пов’язаного з лотереєю, і отримати гарантований дохід без ризику.
Коли особа, що приймає рішення, натрапляє на лотерею, менш пріоритетну, ніж стан, в якому вона в даний момент перебуває, то постає питання, скільки б вона заплатила (в одиницях виміру критерію X) за свою неучасть у цій лотереї (уникнення її).
Страхова сума (СС) – це величина детермінованого еквівалента з протилежним знаком:
| СС(Х) = Х | (4.6) |
Умова схильності до ризику набуває такого вигляду:
| U(M(X)) < M(U(X)), | (4.7) |
тобто корисність сподіваного доходу менше сподіваної корисності. ОПР схильна до ризику. Премія за ризик у випадку схильності до ризику показує, скільки коштів інвестор може додатково отримати або втратити, ризикуючи.
Умова байдужості до ризику набуває такого вигляду:
| U(M(X)) = M(U(X)) | (4.8) |
Премія за ризик у випадку байдужості до ризику завжди дорівнює нулю.






