Знания, информация – одни из важнейших проявлений ценности, обладающие совершенно удивительным свойством тиражируемости, допускающим многократное копирование и использование одной и той же информации без каких-либо ее существенных искажений. Так, однажды созданный проект изделия может далее в массовом порядке редуцироваться в физические копии, а однажды написанное музыкальное произведение может исполняться неограниченное количество раз.
Язык, как и любая другая система, является открытым. Различные языки, взаимодействуя между собой, глубоко проникают друг в друга; они взаимосвязаны и взаимозависимы. Поэтому достаточно четкой границы между ними не существует. В силу этого любое информационное сообщение на каком-либо языке не обладает свойством тиражируемости, поскольку его содержание в процессе передачи от источника к получателю может измениться. Так, одна и та же пьеса различными режиссерами (и тем более актерами) прочитывается и представляется зрителю по-разному. Неожиданный жест или взгляд могут самым решительным образом повлиять на смысл всего действия. Недаром литературные критики очень часто ищут ответ на казалось бы странный вопрос – что хотел сказать на самом деле автор, сказав то-то. Таким образом, информационное сообщение, переданное на некотором языке, может при его приеме породить сонм ассоциативных сообщений на других языках. В силу этого в системе знаний получателя в содержательном и даже смысловом плане может возникнуть отнюдь не точная копия исходного сообщения, а нечто совсем другое. В этом смысле тиражируемость – свойство относительное, касающееся только формы самого информационного сообщения, а не его возможных интерпретаций в системах знаний получателей.
Квантованность рациональной информации означает, что ее прием, хранение, передача и восприятие осуществляются дискретными порциями (квантами). Это свойство является следствием не только квантованности процессов обмена реальных систем, но и дискретности семантического (смыслового) содержания их. Очевидно, наименьшими порциями (квантами) информации являются символы алфавита.
Измеримость информации свидетельствует о существовании ее количественных мер. Хотя данное ее качество можно рассматривать в какой-то мере как внутреннее свойство информации (каким, например, является масса тела в физике), однако количество информации в сообщении зависит и от языка представления, и от выбранного способа измерения. В настоящее время используются (правда, в разной степени) три различных подхода к определению количества рациональной информации: комбинаторный, вероятностный и алгоритмический.
В основе большинства количественных мер информации лежит принцип разнообразия, в соответствии с которым считается, что количество информации, содержащейся в сообщении о предмете X, тем больше, чем выше разница в разнообразии характеристик этого предмета до и после получения сообщения.
Обозначим общее число различных символов алфавита (букв, цифр, поз, жестов и т.п.) языка представления через m. И пусть имеется некоторое сообщение, состоящее из n символов. Тогда число возможных вариантов сообщений такой длины при условии, что появление каждого символа в сообщении есть независимое и равновероятное событие, будет равно
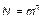. (1.4.1)
Величина N, характеризующая возможное разнообразие сообщений, может рассматриваться в качестве комбинаторной меры количества информации, которое будет содержаться в полученном сообщении.
Однако в реальных ситуациях символы алфавита могут появляться в сообщении с разной вероятностью. Кроме того, само сообщение может также содержать некоторую неопределенность относительно наличия в нем тех или иных символов (например, некоторые буквы оказались неразборчиво написанными). В этом случае для оценки количества информации, содержащейся в сообщении, целесообразно использовать вероятностную меру (меру Шеннона). При статистически независимом появлении символов алфавита в сообщении она определяется следующим образом:
; (1.4.2)
; (1.4.3)
, (1.4.4)
где 
– априорная или апостериорная энтропии сообщения; 
– априорная и апостериорная вероятности j -го значения k -го структурного элемента (характеристики) сообщения.
Единицей измерения количества информации, по Шеннону, при использовании в приведенных выше формулах логарифма по основанию два является бит. Если в указанных формулах используются натуральные логарифмы, то соответствующая единица измерения называется нит.
Комбинаторная и вероятностная меры не являются вполне независимыми. Действительно, вероятность появления конкретного символа из алфавита в сообщении в описанных ранее условиях равна
. (1.4.5)
Используя это выражение и учитывая, что только одно 
либо равно 1, либо равно 0, причем 
для каждого 
, находим, что
. (1.4.6)
Таким образом, I является однозначной функцией N. Однако вполне очевидно, что вероятностная мера количества информации является более общей.
Алгоритмическая мера информации связана с представлением о минимальной длине программы, с помощью которой осуществляется извлечение семантической информации из сообщения.
