Комплексные числа.
Корень уравнения х2+1=0 или  называется мнимой единицей и обозначается буквой i.
называется мнимой единицей и обозначается буквой i.
Таким образом, символ i удовлетворяет условию  .
.
Комплексным числом называется выражение вида a+bi, где а и b – действительные числа, а i – мнимая единица.
Число а называется действительной част ью комплексного числа, а число bi – мнимой частью.
Запись комплексного числа в виде  называется алгебраической формой записи комплексного числа.
называется алгебраической формой записи комплексного числа.
Комплексные числа  и
и 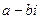 называются сопряженными.
называются сопряженными.
Действия над комплексными числами в алгебраической форме. Суммой двух комплексных чисел  и
и  называется комплексное число
называется комплексное число 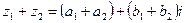
Произведением двух комплексных чисел  и
и  называется комплексное число
называется комплексное число 
Вычитание комплексных чисел вводится как операция, обратная сложению; деление комплексных чисел вводится как операция, обратная умножению.
Правила вычитания и деления комплексных чисел 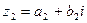 и
и  определяются формулами
определяются формулами

где 
Возведение комплексного числа в степень производится по формулам возведения двучлена в степень, но при этом надо учитывать, что:
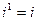 , ,
 , ,
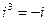 , ,
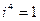 , ,
| 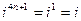 , ,
 , ,
 , ,
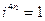
|
Например, 
Пример 1. Найти сумму и произведение комплексных чисел  и
и  .
.
Решение: Сумму находим формальным сложением двучленов  и
и  :
:
 .
.
Произведение находим формальным перемножением двучленов  и
и  с последующей заменой
с последующей заменой  на -1:
на -1:
 .
.
Пример 2. Даны комплексные числа  и
и  . Найти разность
. Найти разность  и частное
и частное  .
.
Решение: Разность находим формальным вычитанием двучленов  и
и  :
:
 .
.
Чтобы найти частное  , умножим числитель и знаменатель этой дроби на число, сопряженное знаменателю
, умножим числитель и знаменатель этой дроби на число, сопряженное знаменателю  :
:
 Пример 3. Наитии комплексное число
Пример 3. Наитии комплексное число  .
.
Решение: Выполнив в знаменателе дроби возведение в степень, получим:
 .
.
Умножив числитель и знаменатель полученной дроби на число, сопряженное знаменателю, т.е на  , получим:
, получим:

Геометрическая интерпретация комплексного числа. Комплексные числа, как и действительные, допускают простую интерпретацию, если вместо координатной прямой использовать координатную плоскость.
Комплексное число  изображается на координатной плоскости точкой М(
изображается на координатной плоскости точкой М(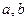 ) или вектором
) или вектором 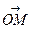 , начало которого совпадает с началом координат, а конец – с точкой М (рис.1).
, начало которого совпадает с началом координат, а конец – с точкой М (рис.1).
 Рис 1
Рис 1
|  Рис. 2
Рис. 2
|  Рис 3.
Рис 3.
|
Сама координатная плоскость называется при этом комплексной плоскостью, ось абсцисс – действительной осью, а ось ординат– мнимой осью.
Модулем комплексного числа называется абсолютная величина вектора, соответствующего этому числу. Для модуля числа  используются обозначения
используются обозначения  ,
,  или
или 
На основании теоремы Пифагора (рис. 1) получается формула:
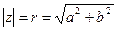 .
.
Например, комплексное число  имеет модуль, равный 10, так как:
имеет модуль, равный 10, так как:
 .
.
Аргументом комплексного числа  называется величина угла φ между положительным направлением действительной оси и вектором, соответствующим этому числу (рис. 1).
называется величина угла φ между положительным направлением действительной оси и вектором, соответствующим этому числу (рис. 1).
Для аргумента числа  используются обозначения φ, агg z или агg
используются обозначения φ, агg z или агg  .
.
Аргумент комплексного числа  в отличие от модуля определяется неоднозначно.
в отличие от модуля определяется неоднозначно.
Так, аргументами числа 5 являются следующие углы  ,
,  ,
,  , и вообще каждый из углов
, и вообще каждый из углов 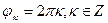 ; аргументом числа
; аргументом числа  – следующие углы:
– следующие углы: 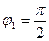 ,
,  ,
,  (рис 2) и вообще каждый из углов
(рис 2) и вообще каждый из углов  .
.
Любые два аргумента комплексного числа отличаются друг от друга на слагаемое, кратное 2  .
.
Аргумент комплексного числа  можно находить так:
можно находить так:
a) найти острый угол  ;
;
b) найти аргумент комплексного числа в зависимости от того, в какой координатной четверти лежит вектор, соответствующий этому числу: в I четверти  ; во II четверти
; во II четверти  ; в III четверти
; в III четверти  ; в IV четверти
; в IV четверти  (или
(или  ).
).
Пример 4. Найти аргумент комплексного числа 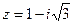 .
.
Решение. Находим угол  . Вектор, соответствующий данному комплексному числу, лежит в IV координатной четверти (рис. 3), поэтому аргументами числа являются каждый из углов
. Вектор, соответствующий данному комплексному числу, лежит в IV координатной четверти (рис. 3), поэтому аргументами числа являются каждый из углов  ,
, 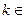 Z.
Z.
Аргументы действительных и чисто мнимых чисел надо находить непосредственно, исходя из их геометрической интерпретации, а не используя приведенное выше правило (тем более, что для чисто мнимых чисел это правило вообще нельзя применять).
Тригонометрическая форма комплексного числа. Пусть дано комплексное число  . Из
. Из  (см. рис. 1) можно выразить действительные числа
(см. рис. 1) можно выразить действительные числа  и
и 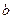 через модуль
через модуль  и аргумент
и аргумент  числа
числа  следующим образом:
следующим образом:  ,
,  . Таким образом, комплексное число можно записать в виде
. Таким образом, комплексное число можно записать в виде
 ,
,
где  – модуль комплексного числа, а
– модуль комплексного числа, а  – один из его аргументов. Представление комплексного числа
– один из его аргументов. Представление комплексного числа  в указанном виде называется тригонометрической формой записи комплексного числа.
в указанном виде называется тригонометрической формой записи комплексного числа.
Для того чтобы перейти от алгебраической формы записи комплексного числа  к тригонометрической, достаточно найти его модуль и один из аргументов. Аргумент комплексного числа
к тригонометрической, достаточно найти его модуль и один из аргументов. Аргумент комплексного числа  можно находить из системы
можно находить из системы 
Пример 5. Записать число  в тригонометрической форме.
в тригонометрической форме.
Решение. Находим модуль
 .
.
Находим угол
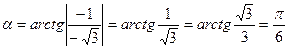 .
.
Вектор, соответствующий данному комплексному числу, лежит в III координатной четверти (рис. 4), поэтому одним из аргументов является 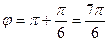 . Следовательно,
. Следовательно,
 .
.
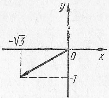 Рис 4.
Рис 4.
| Для того чтобы перейти от тригонометрической формы записи комплексного числа  к алгебраической, достаточно найти действительные числа к алгебраической, достаточно найти действительные числа  и и 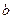 по формулам по формулам  , ,  . .
|
Пример 6. Записать число  в алгебраической форме.
в алгебраической форме.
Решение. Сначала найдем  и
и  :
: 
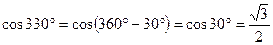 ,
,  .
.
Тогда  ,
,  . Следовательно,
. Следовательно, 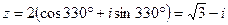 .
.
Действия над комплексными числами, заданными в тригонометрической форме. Если
 и
и  , то
, то
 ,
,
 .
.
Если  , то
, то
 ,
,
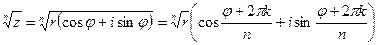 ,
,
где  – арифметический корень,
– арифметический корень,  .
.
Пример 7. Даны комплексные числа  и
и 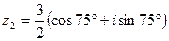 . Найти их произведение
. Найти их произведение  и частное
и частное  . Ответ записать в алгебраической форме.
. Ответ записать в алгебраической форме.
Решение. Применяя правила умножения и деления комплексных чисел, имеем

 .
.
Пример 8. Вычислить  .
.
Решение. Находим
 .
.
Пример 9. Вычислить  .
.
Решение. Запишем число  в тригонометрической форме. Находим
в тригонометрической форме. Находим
 ,
,
 ,
,
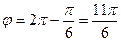 или
или  .
.
Тогда  и, значит,
и, значит,


Пример 10. Вычислить 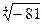 . Ответ записать в тригонометрической и алгебраической формах.
. Ответ записать в тригонометрической и алгебраической формах.
Решение. Запишем число  в тригонометрической форме:
в тригонометрической форме: 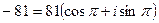 . Следовательно,
. Следовательно,

где  При
При  получим:
получим:




Показательная форма комплексного числа. Рассматривая функцию  для комплексного переменного, Эйлер установил замечательное соотношение
для комплексного переменного, Эйлер установил замечательное соотношение  которое называется формулой Эйлера.
которое называется формулой Эйлера.
Из этой формулы следует, что каждое комплексное число  можно записать в форме
можно записать в форме  которая называется показательной формой записи.
которая называется показательной формой записи.
Над комплексными числами, заданными в показательной форме, удобно производить умножение и деление, возведение в натуральную степень и извлечение корня:




Пример 11. Представить число  в алгебраической форме.
в алгебраической форме.
Решение. По условию,  откуда
откуда


Значит, 
Пример 12. Выполнить действия и записать ответ в тригонометрической и показательной формах

Решение. Сначала выполним действия:


Теперь запишем число в тригонометрической и показательной формах, для чего найдем его модуль и аргумент

Тогда 
Производная и ее приложения.
. Понятие производной является одним из фундаментальных понятий математики. Многие задачи как самой математики, так и естествознания и техники приводят к этому понятию.
Пусть функция  определена в промежутке
определена в промежутке  . Возьмем из этого промежутка фиксированное значение аргумента
. Возьмем из этого промежутка фиксированное значение аргумента 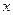 и придадим ему приращение
и придадим ему приращение  так, чтобы новое значение аргумента
так, чтобы новое значение аргумента 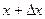 принадлежало этому промежутку. Тогда значение функции
принадлежало этому промежутку. Тогда значение функции 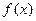 заменится новым значением
заменится новым значением  , т.е. функция получит приращение
, т.е. функция получит приращение  .
.
Предел отношения приращения функции  к вызвавшему его приращению аргумента
к вызвавшему его приращению аргумента  при стремлении
при стремлении  к нулю, т.е.
к нулю, т.е.

называется производной функции  по аргументу
по аргументу 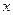 в точке
в точке 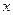 .
.
Производная обозначается одним из символов:  а ее значение при
а ее значение при 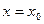 обозначается
обозначается 
Операция нахождения производной называется дифференцированием.
Если функция 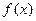 имеет производную в точке
имеет производную в точке 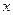 , то она называется дифференцируемой в этой точке.
, то она называется дифференцируемой в этой точке.
Если функция 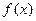 имеет производную в каждой точке промежутка
имеет производную в каждой точке промежутка  , то говорят, что эта функция дифференцируема на этом промежутке.
, то говорят, что эта функция дифференцируема на этом промежутке.
Производная сложной функции. Пусть  , где
, где  является не независимой переменной, а функцией независимой переменной
является не независимой переменной, а функцией независимой переменной  . Таким образом,
. Таким образом,  .
.
В этом случае функция  называется сложной функцией
называется сложной функцией 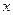 , а переменная
, а переменная  – промежуточным аргументом.
– промежуточным аргументом.
Производная сложной функции находится на основании следующей теоремы: если  и
и  – дифференцируемые функции своих аргументов, то производная сложной функции
– дифференцируемые функции своих аргументов, то производная сложной функции  существует и равна произведению производной функции
существует и равна произведению производной функции  по промежуточному аргументу
по промежуточному аргументу  на производную промежуточного аргумента
на производную промежуточного аргумента  по независимой переменной
по независимой переменной 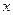 :
:  .
.
Эта теорема распространяется и на сложные функции, которые задаются с помощью цепочки, содержащей три звена и более.
Например, если 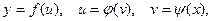 т.е.
т.е.  , то
, то 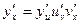 .
.
Формулы дифференцирования. Во всех приведенных ниже формулах буквами  и
и  обозначены дифференцируемые функции независимой переменной
обозначены дифференцируемые функции независимой переменной 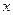 :
:  , а буквами
, а буквами  –постоянные:
–постоянные:
1. 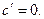 2.
2.  3.
3. 
| 4.  5.
5. 
| 6. 
|
Остальные формулы записаны как для функций независимой переменной, так и для сложных функций:
7. 
| 7а. 
|
8. 
| 8а. 
|
9. 
| 9а. 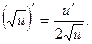
|
10. 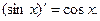
| 10а. 
|
11. 
| 11а. 
|
12. 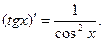
| 12а. 
|
13. 
| 13а. 
|
14. 
| 14а. 
|
15. 
| 15а. 
|
16. 
| 16а. 
|
17. 
| 17а.  где где 
|
При решении приведенных ниже примеров сделаны подробные записи. Однако следует научиться дифференцировать без промежуточных записей.






