Первое начало термодинамики

Предположим, что некоторая система за счет поглощения теплоты Q переходит из исходного состояния 1 в конечное состояние 2. В общем случае эта теплота расходуется на изменение внутренней энергии системы DU и на совершение системой работы против внешних сил W:

Q_1-2 = ΔU_1-2 +W_1-2.

Приведенное уравнение выражает закон сохранения энергии, который называется также первым законом или началом термодинамики. Согласно этому закону:

1. Энергия не может ни создаваться, ни исчезать, а только переходит из одной формы в другую. Например, внутренняя энергия, содержащаяся в веществе, может превращаться в тепловую, световую (пламя), электрическую (химический аккумулятор) и т.д. Отсюда следует, что в изолированной системе запас энергии остается постоянным.

2. Вечный двигатель первого рода невозможен, т.е. невозможно создать машину, которая бы производила механическую работу, не затрачивая на это соответствующего количества энергии.

3. Согласно этому закону внутренняя энергия не зависит лт способа проведения процесса, а определяется только начальнам и конечным состоянием системы, т.е. внутренняя энергия является функцией состояния.

ΔU = U₂-U₁

Теплота представляет собой количественную меру хаотического движения частиц данной системы или тела. Энергия более нагретого тела самопроизвольно в форме теплоты передается менее нагретому телу. При этом не происходит перенос вещества от одной системы к другой или от одного тела к другому.

Работа является количественной мерой направленного движения частиц, мерой энергии, передаваемой от одной системы к другой за счет перемещения вещества под действием тех или иных сил.

Вообще, следует отметить, что ни запасом теплоты, ни запасом работы система не обладает. Система обладает лишь запасом внутренней энергии, а теплота и работа показывают, каким способом изменяется внутренняя энергия системы. Теплота и работа зависят от пути протекания процесса, и поэтому не обладают свойствами функции состояния, как «запас теплоты» системы и «запас работы», которую может совершить система.

Единицей измерения работы, теплоты и внутренней энергии в системе СИ служит джоуль (Дж). 1 джоуль – это работа силы в 1 ньютон на расстоянии 1 м (1 Дж = 1 Н×м = 1 кг×м²/с²). В старой химической литературе широко использовалась единица количества теплоты и энергии калория (кал). 1 Калория – это такое количество теплоты, которое необходимо для нагревания 1 г воды на 1°C. 1 кал = 4,184 Дж» 4,2 Дж. Теплоты химических реакций удобнее выражать в килоджоулях или килокалориях: 1 кДж = 1000 Дж, 1 ккал = 1000 кал.

Для химических реакций под работой против внешних сил в основном подразумевается работа против внешнего давления или работа расширения газа.

Рассмотрим газ, находящийся в цилиндре с поршнем, позволяющем менять объем газа (рис 2.1). Отметим, что слово «газ» здесь совершенно условно. Это может быть жидкость, кристалл и вообще любое тело. Цилиндр контактирует с нагревателем или холодильником, который может сообщать газу тепло или отбирать его.Пусть на поршень оказывается внешнее давление (р), величина которого может быть любой.

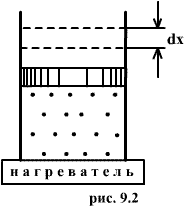
Рис. 2.1. Схема работы газа

Работа над газом выполняется внешними силами при его сжатии. Работа самого газа выполняется при его расширении. Пусть газ расширяется так, что поршень на рис. 4.1 поднимается на величину dx. Тогда газ выполнит работу

,

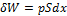где S – площадь поршня. Получим:

.

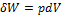Эта величина называется элементарной работой газа. Работа при расширении газа от объема V₁ до V₂ будет равна

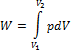
или при постоянном давлении

.

Если по одной оси отложить объем газа, по другой – его давление (плоскость p–V), то работа будет изображаться площадью под кривой p(V) (рис. 2.2).

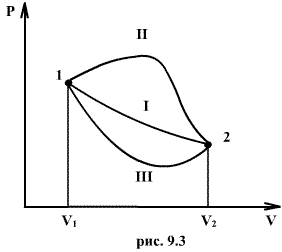
Рис. 2.2. График работы расширения газа

Процесс расширения от объемаV₁до объемаV₂может происходить различным образом: например, можно при этом изолировать газ от нагревателя или, наоборот, нагревать газ и т.д. Иначе говоря, при перемещении из точки 1 в точку 2 в газе могут происходить различные процессы, даже если зафиксировано начальное и конечное состояния. В каждом процессе работа будет иметь свое значение, так как площадь под кривой процесса будет различной (кривые I, II, и III на рис. 2.2). Таким образом, выполняемая газом работа зависит от процесса, который с ним происходит. Обычно говорят, что «работа газа есть функция процесса или функция пути».Заметим, что работа положительна, если она выполняется газом, и отрицательна, если внешние силы выполняют ее над газом.