1.Случайные события. Изучение каждого явления в порядке наблюдения или производства опыта связано с осуществлением некоторого комплекса условий (испытаний). Всякий результат или исход испытания называется событием.
Если событие при заданных условиях может произойти или не произойти, то оно называется случайным. В том случае, когда событие должно непременно произойти, его называют достоверным, а в том случае, когда оно заведомо не может произойти – невозможным.
События называют несовместными, если каждый раз возможно появление только одного из них. События называются совместными, если в данных условиях появление одного из этих событий не исключает появление другого при том же испытании.
События называются противоположными, если в условиях испытания они, являясь единственными его исходами, несовместны.
Вероятность события рассматривается как мера объективной возможности появления
случайного события.
2.Классическое определение вероятности. Вероятностью события А называется отношение числа исходов m, благоприятствующих наступлению данного события А, к числу n всех исходов (несовместных, единственно возможных и равновозможных), т.е.
(1.40)
Вероятность любого события не может быть меньше нуля и больше единицы, т.е. 
Невозможному событию соответствует вероятность Р(А) = 0, а достоверному – вероятность Р(А) = 1.
Задача. В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?
Общее число различных исходов есть n = 1000. Число исходов, благоприятствующих получению выигрыша, составляет m = 200. Согласно формуле (1.40), получим Р(А) = 200/1000 = 1/5 = 0,2. ·
Задача. Из урны, в которой находятся 5 белых и 3 черных шара, вынимают один шар. Найти вероятность того, что шар окажется черным.
Обозначим событие, состоящее в появлении черного шара, через А. Общее число случаев n = 5 + 3 = 8. Число случаев m, благоприятствующих появлению события А, равно 3. По формуле (1.40) получим Р(А) = m/n = 3/8 = 0,375. ·
Задача. Из урны, в которой находятся 12 белых и 8 черных шаров, вынимают наудачу два шара. Какова вероятность того, что оба шара окажутся черными?
Обозначим событие, состоящее в появлении двух черных шаров, через А. Общее число возможных случаев n равно числу сочетаний из 20 элементов (12 + 8) по два:
Число случаев m, благоприятствующих событию А, составляет
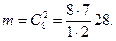
По формуле (1.40) находим вероятность появления двух черных шаров:
·
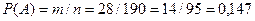Задача. В партии из 18 деталей находятся 4 бракованных. Наугад выбирают 5 деталей. Найти вероятность того, что из этих 5 деталей две окажутся бракованными.
Число всех равновозможных независимых исходов n равно числу сочетаний из 18 по 5, т.е.
Подсчитаем число исходов m, благоприятствующих событию А. Среди 5 взятых наугад деталей должно быть 3 качественных и 2 бракованных. Число способов выборки двух бракованных деталей из 4 имеющихся бракованных равно числу сочетаний из 4 по 2:
Число способов выборки трех качественных деталей из 14 имеющихся качественных равно
Любая группа качественных деталей может комбинироваться с любой группой бракованных деталей, Поэтому общее число комбинаций m составляет
Искомая вероятность события А равна отношению числа исходов m, благоприятствующих этому событию, к числу n всех равновозможных независимых исходов:
·
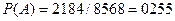