Непосредственное интегрирование основано на прямом использовании таблицы интегралов. Здесь могут представиться следующие случаи:
1) данный интеграл находится непосредственно по соответствующему табличному интегралу;
2) данный интеграл после применения свойств 3 и 4 приводится к одному или нескольким табличным интегралам;
3) данный интеграл после элементарных тождественных преобразований над подынтегральной функцией и применения свойств 3 и 4 приводится к одному или нескольким табличным интегралам.
Найти следующие интегралы:
1. 1) 
2) 
3) 
4) 
5) 
1) На основании свойства 4 постоянный множитель 5 выносим за знак интеграла и, используя формулу 1.20., получим 
·
2) Используя свойство 4 и формулу 1.21., получим 
·
Проверка: 
Получили подынтегральное выражение; следовательно, интеграл найден правильно.
3) Используя свойства 3 и 4 и формулы 1.21. и 1.20., имеем 
Постоянная интегрирования С равна алгебраической сумме трех постоянных интегрирования, так как каждый интеграл имеет свою произвольную постоянную 
4) 
·
5) 
·
2. 1) 
2) 
.
1) 
·
2) 
·
3. 1) 
2) 
3) 
1) По формуле 1.22. находим 
·
2) Так как 
, то 
·
3) Так как 
, то 
·
Знак абсолютной величины не пишем, так как при любом значении х выражение 
4. 1)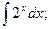 
2) 
3) 
1) По формуле 1.23. при 
получим 
·
2) Так как 
, то
·
3) Так как 
, то 
·
5. 1) 
2) 
3) 
1) так как 
то 
Следовательно,
·
2) Так как 
то
·
3) Так как 
, то 
·
6. 1) 
2) 
3) 
4) 
1) По формуле 1.27. находим 
·
2) Так как 
то 
. Следовательно,
·
3) По формуле 1.18. находим 
·
4) Так как 
, то 
·
7. 1) 
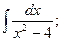2) 
1) По формуле 1.29. получаем 
·
2) По формуле 1.30. находим 
·
8. 1) 
2) 
3) 
4) 
1) По формуле 1.31. находим 
·
2) 
·
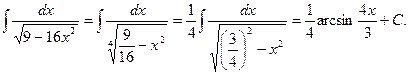3) По формуле 1.32. находим 
·
4) 
·
Определенный интеграл.
Определенный интеграл и его непосредственное вычисление.
Пусть функция 
определена на отрезке 
. Разобьем этот отрезок на n частей точками 
, выберем на каждом элементарном отрезке 
произвольную точку 
и обозначим через 
длину каждого такого отрезка. Интегральной суммой для функции на отрезке называется сумма вида
Определенным интегралом от функции , непрерывной на отрезке называется предел интегральной суммы при условии, что длина наибольшего из элементарных отрезков стремится к нулю:
Для любой функции , непрерывной на отрезке , всегда существует определенный интеграл 
. Для вычисления определенного интеграла от функции в том случае, когда можно найти соответствующий определенный интеграл 
, служит формула Ньютона – Лейбница:
т.е. определенный интеграл равен разности значений первообразной при верхнем и нижнем пределах интегрирования.
Вычислить следующие определенные интегралы:
1. 1) 
2) 
3) 
По формуле Ньютона – Лейбница получаем:
1) 
·
2) 
·
3) 
·
2. 1) 
2) 
1) 
·
2) 
·
3. 1) 
2) 
1) 
·
2) 
·
4. 1) 
2) 
1) 
·
2) 
·
