1. Число А называется пределом функции 
при 
, если для любого числа 
можно указать такое 
, что для любого 
, удовлетворяющего неравенству 
, выполняется неравенство 
. В этом случае пишут 
. Если число А1 (число А2) есть предел функции 
при х, стремящемся к 
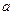так, что х принимает только значения, меньшие (большие) 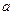, то А1 (А2) называется левым (правым) пределом функции в точке 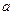. При этом соответственно пишут 
2. Функция называется бесконечно малой при , если 
.
3. Функция называется бесконечно большой при , если 
, или 
, или 
.
Отметим свойства бесконечно малых и бесконечно больших функций.
· Если функция и 
– бесконечно малые при , то их сумма 
при также является бесконечно малой.
· Если функция – бесконечно малая при , а 
– ограниченная функция, то их произведение 
есть функция бесконечно малая.
Следствие. Произведение конечного числа бесконечно малых функций есть величина бесконечно малая.
· Если при функция имеет конечный предел , а функция – бесконечно большая, то
· Если функция – бесконечно малая при , то функция 
– бесконечно большая, причем предполагается, что в окрестности точки а функция не обращается в нуль. Наоборот, если при функция – бесконечно большая, то функция 
– бесконечно малая. Между бесконечно малой функцией и функцией, имеющей конечный предел, существует следующая зависимость. Если функция имеет конечный предел при , то ее можно представить в виде суммы постоянной и бесконечно малой функции при . Наоборот, если функция может быть представлена в виде суммы постоянной и бесконечно малой функции при , то эта функция имеет конечный предел при , который равен значению постоянной.
4. Теорема 1. Если существуют пределы функций и , то существует также и предел их суммы, равный сумме пределов функций и :
Теорема 2. Если существуют пределы функций и при , то существует также и предел их произведения, равный произведению пределов функций и :
Теорема 3. Если существуют пределы функций и при и предел функции отличен от нуля, то существует также предел отношения 
, равный отношению пределов функций и :
Следствия.
1. Постоянный множитель можно вынести за знак предела: 
2. Если n – натуральное число, то 
3. Предел многочлена (целой рациональной функции)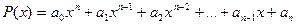 
4. Предел дробно-рациональной функции 
при равен значению этой функции при 
, если 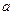принадлежит области определения функции, т.е. 
.
Вычислите пределы:
1. 1) 
; 2) 
.
1) По правилу нахождения предела многочлена находим
.·
2) Так как при 
знаменатель дроби отличен от нуля, то по правилу нахождения предела дробно-рациональной функции получим
·
2. 1) 
; 2) 
; 3) 
.
1) Здесь предел делителя равен нулю: 
. Следовательно, теорему о пределе частного применить нельзя. Так как 
, то 
при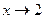 
есть величина бесконечно малая, а обратная ей величина 
– бесконечно большая. Поэтому при 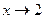произведение 
есть величина бесконечно большая, т.е. 
·
2) Здесь пределы числителя и знаменателя при 
равны нулю. Непосредственной подстановкой вместо аргумента его предельного значения вычислить предел нельзя, так как при получается отношение двух бесконечно малых величин. Разложим числитель и знаменатель на множители, чтобы сократить дробь на общий множитель стремящийся к нулю, и, следовательно, сделать возможным применение теоремы 3. Нужно иметь в виду, что здесь не производится сокращение на нуль, что недопустимо. По определению предела функции аргумент х стремится к своему предельному значению, никогда не принимая этого значения; поэтому до перехода к пределу можно произвести сокращение на множитель, стремящийся к нулю. Имеем
·
3) Пределы числителя и знаменателя при 
равны нулю: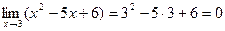 
, 
. Разложим квадратный трехчлен в числителе на линейные множители по формуле 
, где 
и 
– корни трехчлена. Разложив на множители и знаменатель, сократим дробь на 
. Используя следствие 4, получим
·
3. 1) 
; 2) 
; 3) 
.
1) При 
знаменатель 
неограниченно растет, т.е. является величиной бесконечно большой, а обратная величина 
– бесконечно малой. Произведение 
бесконечно малой на ограниченную величину (постоянная – частный случай ограниченной величины) есть величина бесконечно малая, и предел ее при равен нулю. Следовательно, 
·
2) При числитель и знаменатель – величины бесконечно большие. Поэтому при непосредственном применении теоремы 3 получаем выражение 
, которое представляет собой неопределенность. Для вычисления предела этой функции можно числитель и знаменатель разделить на х:
·
(при слагаемые 
и 
– величины бесконечно малые и, следовательно, их пределы равны нулю).
3) Разделим числитель и знаменатель на наивысшую степень аргумента в знаменателе, т.е. на 
:
При имеем
и 
Так как знаменатель есть величина ограниченная, то
·
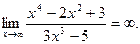