Изучение измерительных приборов 0м
1. Природа и виды погрешностей. Что называется прямыми и косвенными измерениями? Для всех видов погрешностей дать определение. Для систематических − указать два вида этих погрешностей. Для случайных − указать четыре причины возникновения этих погрешностей. С какими видами погрешностей столкнулись вы в своей лабораторной работе? (объяснить свои записи в тетради).
2. Абсолютная и относительная погрешности измерений. Закон распределения Гаусса и функция распределения Стьюдента. Среднее квадратичное отклонение s.
3. Вычисление случайных погрешностей прямых измерений (при малом и большом числе измерений). Оценка надежности результата. Дать определения следующим понятиям: доверительная вероятность Р, коэффициент надежности a, доверительный интервал.
4. Вычисление случайных погрешностей косвенных измерений. Привести пример вывода абсолютной и относительной погрешности косвенных измерений (объема детали, момента инерции диска). (Примечание: примеры выводов формул приводятся в методических указаниях к данной лабораторной работе).
5. Устройство и принцип работы штангенциркуля и микрометра, их абсолютные погрешности измерений. Продемонстрировать умение пользоваться приборами (снимать показания).
Критерии оценки:
оценка «зачтено» выставляется студенту, если студент ответил на все поставленные вопросы и подготовил по ним конспект;
оценка «не зачтено» выставляется студенту, если студент не ответил на все поставленные вопросы и (или) не подготовил по ним конспект.
Изучение законов динамики поступательного движения 41м.
1. Инерциальные и неинерциальные системы. Первый закон Ньютона.
2. Консервативные и неконсервативные силы. Второй и третий законы Ньютона.
3. Импульс силы, импульс тела (количество движения). Второй закон Ньютона в импульсной форме.
4. Замкнутые механические системы. Закон сохранения импульса.
5. Виды механической энергии. Закон сохранения энергии.
6. Упругий и неупругий удары. Умение решать задачи на законы сохранения энергии и импульса.
Пример.
Два тела массами m1 = 1 кг и m2 = 2 кг движутся по гладкой горизонтальной поверхности во взаимно перпендикулярных направлениях со скоростями v1 = 10 м/с и v2 = 15 м/с соответственно. После соударения первое тело остановилось. Какое количество теплоты выделится при ударе?
Дано: Решение
m1 = 1 кг Поверхность гладкая, значит на систему тел m1 и m2 в горизонтальном
m2 = 2 кг направлении внешние силы не действуют и можно воспользоваться за-
v1 = 10 м/с коном сохранения импульса:
v2 = 15 м/с 
, (1)
v´1 = 0 где v – скорость второго тела после удара.
_________ Введем оси x и y, как указано на рисунке и спроецируем на них данное
Q -? векторное уравнение:
OX) m1v1 = m2vx (2)
OY) m2v2 = m2vy, (3)
где vx и vy проекции неизвестной скорости 
.
Найдем их:
; 
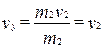(4,5)
Количество теплоты, которое выделится при ударе будет опреде-ляться как разность кинетической энергии системы тел до удара и после удара:
(6)
Ж
Ответ: при ударе выделилось 25 Дж теплоты.
Определение коэффицента трения скольжения 44м.
1. Рассказать о видах трения: трении покоя, внешнем и внутреннем трении, сухом и жидкостном трении, трении скольжения и трении качения.
2. Природа сил трения. Сущность молекулярно-механической теории трения.
3. Продемонстрировать знание законов сухого трения. Закон трения скольжения (закон Амонтона). Более точный закон трения скольжения (при скольжении по очень гладкой поверхности). Приближенный закон Кулона для вычисления силы трения качения.
4. Объяснить методику определения коэффициента трения скольжения в данной работе.
5. Решить задачу.
Пример. Определить ускорение тела, соскальзывающего с наклонной плоскости, если угол наклона плоскости a =30°, а коэффициент трения между телом и наклонной плоскостью 0,3.
Дано: Решение
a =30° Эта задача на II закон Ньютона, алгоритм решения таких задач известен:
μ = 0,3 1. Расставим силы, действующие на тело:
_______ 
- сила притяжения;
а -? 
- сила нормальной реакции опоры;
- сила трения.
2. Запишем II закон Ньютона в векторном виде:
3. Запишем это уравнение в скалярном виде, спроецировав все векторные величины на выбранные оси. Ось x направим вдоль наклонной плоскости, а ось y – перпендикулярно ей.
OX) mg sin α - Fтр = mа (1)
OY) – mg cos α + N = 0 (2)
Учтем, что Fтр = μ·N (3)
Перепишем уравнения (1) и (2) в следующем виде с учетом (3):
mg sin α − μ·N = mа
mg cos α = N
Подствавив одно уравнение в другое, получим:
mg sin α − μ·mg cos α = mа
Отсюда: α = sin α − μ cos α
α = 0,24 м/с2.
Ответ: α = 0,24 м/с2.
Определение модуля упругости методом растяжения 12м.
1. Кристаллические и аморфные тела. Их физические свойства.
2. Рассказать о видах деформации: упругой и пластической, о деформации при растяжении и сжатии твердого тела, сдвиге, изгибе, кручении.
3. Графическое изображение упругой и пластической деформации. Предел упругости, предел прочности.
4. Сила упругости. Записать закон Гука для пружины и стержня при продольном растяжении.
5. Привести формулы модуля Юнга и коэффициента Пуассона, объяснить, что характеризует данная величина.
6. Записать формулы работы и потенциальной энергии сжатой пружины.
Измерение момента инерции тел при помощи крестообразного маятника 8м.
1. Кинематика вращательного движения твердого тела: формулы по определению угловых величин − скорости, ускорения, перемещения. Связь угловых и линейных величин. Уравнения движения при равномерном, равноускоренном и равнозамедленном движении материальной точки по окружности.
2. Привести формулы по определению момента силы, момента инерции материальной точки и системы материальных точек, абсолютно твердого тела; назвать единицы измерения данных физических величин.
3. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси (вывод).
4. Уравнения моментов инерции тел правильной геометрической формы − стержня, кольца, цилиндра, шара для оси вращения, проходящей через центр масс тел. Привести пример вывода уравнения момента инерции для одного из перечисленных тел.
5. Теорема Штейнера и ее применение. Решить задачу по теме.
Пример. Найти моменты инерции маховика в виде сплошного диска массой 0,5 кг и радиусом 50 см в трех случаях: 1) когда ось вращения проходит через центр масс диска; 2) когда ось вращения параллельна той, которая бы проходила через центр масс диска, но находится на расстоянии 20 см от него; 3) когда ось вращения проходит через точку лежащую на ободе маховика.
Дано: Решение
m = 0,5 кг В первом случае момент инерции находится по известной формуле:
R = 0,5 м I = mR2/2
a2 = 0,2 м I = 0,5·(0,5)2/2 = 0,0625 кг·м2.
a3 = 0,5 м Во втором случае применим теорему Штейнера:
_______ I = Iс + ma2,
а -? где Iс − момент инерции для оси вращения, проходящей через центр масс (мы его рассчитали в задании 1),
a − расстояние от оси вращения до центра масс.
I = 0,0625 + (0,5(0,2)2) = 0,0825 кг·м2.
В третьем случае также применим теорему Штейнера, только расстояние от оси вращения до центра масс будет равно a3 = 0,5 м:
I = 0,0625 + (0,5(0,5)2) = 0,1875 кг·м2.
Ответ: I1 = 0,0625 кг·м2, I2 = 0,0825 кг·м2, I3 = 0,1875 кг·м2.
Примечание: результаты можно округлять до сотых.
