Формула Грина для плоскости

Если L - граница области D и функции непрерывны, вместе со своими частными производными 1-го порядка, в замкнутой области D, то справедлива формула Грина обход контура выбирается положительным

Пример 33. Вычислить криволинейный интеграл непосредственно и с помо­щью формулы Грина

где L - периметр треугольника с вершинами А (-1;0), В (0,2) и С (2;0).

Решение. Сделаем рисунок 39. Составим уравнение АВ:

Составим уравнение ВС:

Составим уравнение СА:

Рис. 39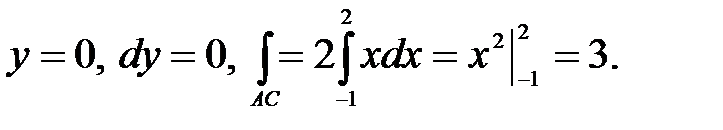

Следовательно,

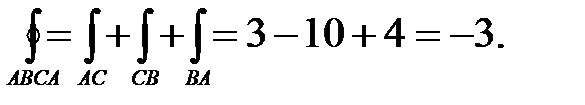
Вычислим криволинейный интеграл с помощью формулы Грина

3 3.5. Восстановление функции по ее полному дифференциалу

Если известен полный дифференциал функции двух переменных где то ее можно найти интегрируя по любой линии между произвольной фиксированной точкой и переменной точкой

(3.1)

Обычно в качестве линии интегрирования АМ берется ломаная AN₁M или AN₂M со звеньями, параллельными осям координат (рис. 40). При этом криволинейный интеграл наиболее просто выражается через обыкновенные интегралы, и формула (3.1) преобразуя к виду

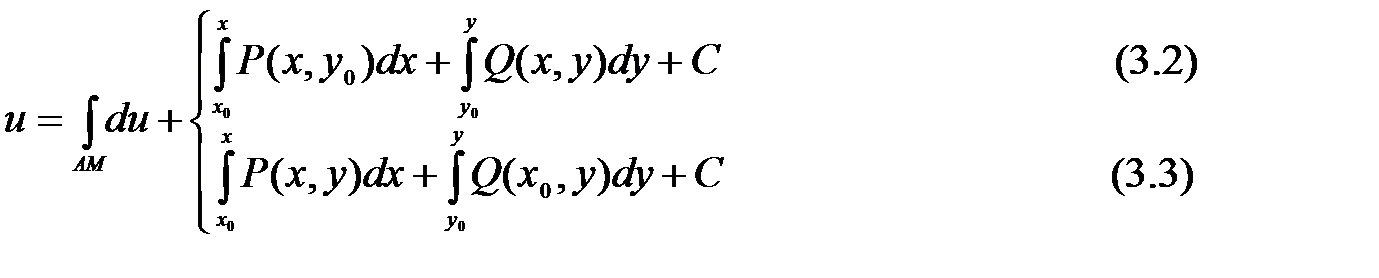
Во многих случаях можно найти функцию по ее полному дифференциалу иначе.

Поскольку полный дифференциал равен сумме частных дифференциалов то интегрируя каждый из них отдельно, найдем два выражения искомой функции :

а) считая у постоянной;

б) считая х постоянной;

где и - неизвестные функции.

Беря все известные члены из первого выражения и дописав к ним недостающие члены, зависящие только от у, из второго выражения получим функцию u.

y

Решение такой задачи легко проверить: если функция u найдена верно, то ее полный дифференциал, найденный по формуле должен быть тождествен данному полному дифференциалу

 

N2(x0,y)

M(x,y)

 

 

 

x

A(x0,y0)

N1(x,y0)

 

Рис. 40

Пример 34. Проверить, что данное выражение является полным дифференциалом функции , и найти u:

1)

2)

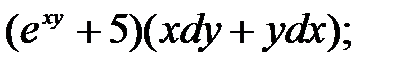
3)

Решение.

1) Обозначим коэффициенты при дифференциалах и найдем и Так как здесь и непрерывны, то заданное выражение является полным дифференциалом некоторой функции u.

Найдем эту функцию по формуле (3.2), выбрав точку А в начале координат О (0,0)

2) Преобразуем заданное дифференциальное выражение к виду и найдем :

Условие выполнено. Заданное выражение есть полный дифференциал некоторой функции

Найдем эту функцию по формуле (3.3):

где

3) В начале находим частные производные

и убеждаемся, что они тождественно равны и что заданное выражение есть полный дифференциал некоторой функции Затем найдем эту функцию вторым способом, интегрируя каждый частный дифференциал и отдельно.

а) считая у постоянной;

б) считая х постоянной.

Объединяя эти два выражения – дописав к известным членам первого выражения недостающий член, зависящий только от у, из второго выражения получим одну из первообразных функций, а прибавив к ней произвольную постоянную С, получим общее выражение первообразной функции для заданного полного дифференциала

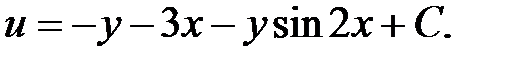
Пример 35.

Дано: dU = 2xydx + x²dy.

Найти U(x,y).

Решение.

Выбираем начальную точку М₀ - пусть М₀(1,0), а путь интегрирования М₀M - по звеньям ломаной М₀AM, тогда

 

 

Задача 1. Изменить порядок интегрирования.

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

Задача 2. Вычислить двойные интегралы:

1. а) ; .

б) ; .

2. а) ; .

б) ; .

3. а) ; .

б) ; .

4. а) ; .

б) ; .

5. а) ; .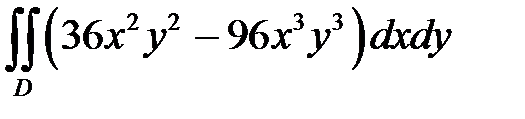

б) ; .

6. а) ; .

б) ; .

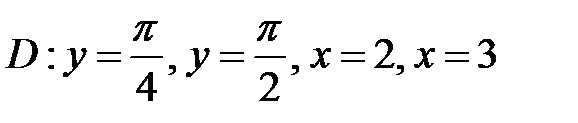7. а) ; .

б) ; .

8. а) ; .

б) ; .

9. а) ; .

б) ; .

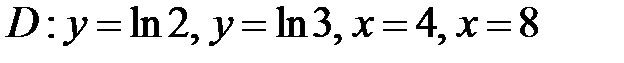10. а) ; .

б) ; .

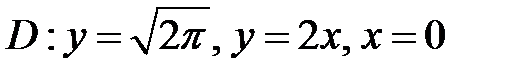11. а) ; .

б) ; .

12. а) ; .

б) ; .

13. а) ; .

б) ; .

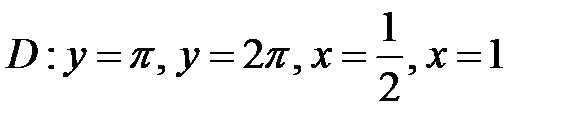14. а) ; .

б) ; .

15. а) ; .

б) ; .

16. а) ; .

б) ; .

17. а) ; .

б) ; .

18. а) ; .

б) ; .

19. а) ; .

б) ; .

20. а) ; .

б) ; .

 

Задача 3. Вычислить тройные интегралы:

1. а) ; .

б) ; .

2. а) ; .

б) ; .

3. а) ; .

б) ; .

4. а) ; .

б) ; .

5. а) ; .

б) ; .

6. а) ; .

б) ; .

7. а) ; .

б) ; .

8. а) ; .

б) ; .

9. а) ; .

б) ; .

10. а) ; .

б) ; .

11. а) ; .

б) ; .

12. а) ; .

б) ; .

13. а) ; .

б) ; .

14. а) ; .

б) ; .

15. а) ; .

б) ; .

16. а) ; .

б) ; .

17. а) ; .

б) ; .

18. а) ; .

б) ; .

19. а) ; .

б) ; .

20. а) ; .

б) ; .

Задача 4. Найти площадь фигуры, ограниченной данными линиями.

1.

2. .

3. .

4. .

5. .

6. .

7. .

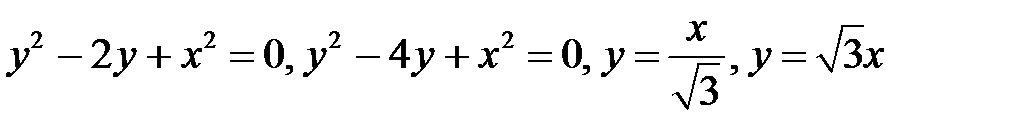8.

9.

10. .

11. .

12. .

13. .

14.

15.

16.

17.

18.

19.

20.

Задача 5. Пластинка D задана ограничивающими ее плоскостями, µ- поверхностная плотность. Найти массу пластинки.

1. .

2. .

3. .

4.

5.

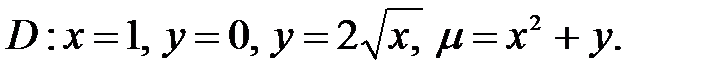
6.

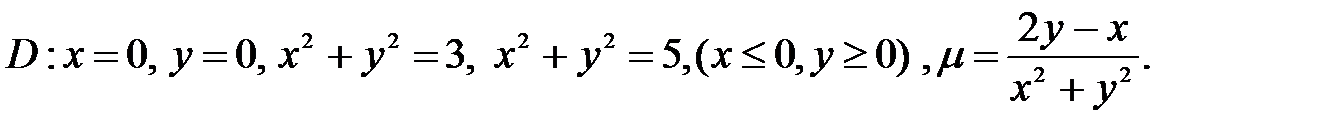
7. .

8.

9.

10.

11. .

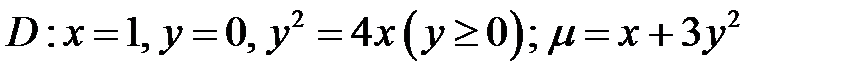12.

13.

14.

15. .

16. .

17.

18. .

19. .

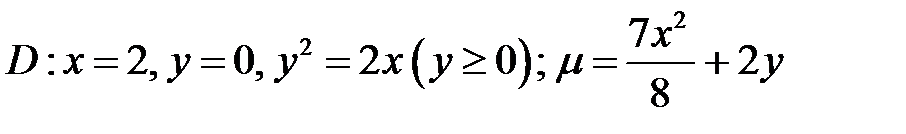20. .

Задача 6. Найти объем тела, заданного ограничивающими его поверхностями.

1. .

2. .

3. .

4.

5.

6.

7. .

8. .

9.

10.

11.

12. .

13. .

14. .

15. .

16. .

17. .

18. .

19. .

20. .

Задача 7. Тело V задано ограничивающими его поверхностями, m - плотность. Найти массу тела.

1.

2.

3.

4.

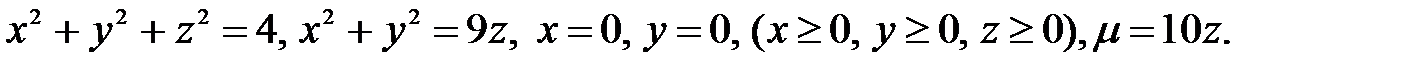
5.

6.

7.

8.

9.

10.

11. .

12. .

13.

14.

15. .

16. .

17. .

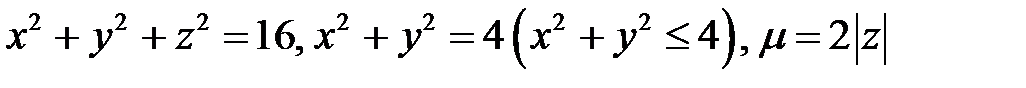18.

19.

20.

Задача 8. Вычислить интегралы

1. по дуге синусоиды от до .

2. по кривой от точки до точки .

3. 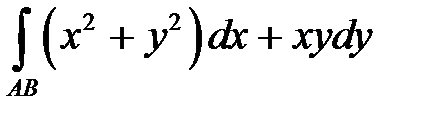по кривой от точки 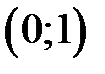до точки .

4. по параболе от точки до точки .

5. по параболе от точки до точки .

6. по кривой от точки до точки .

7. по кривой от точки до точки .

8. по кривой , , .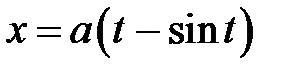

9. , где - контур треугольника с вершинами , , .

10. , где - прямая, соединяющая точки и .

11. , где - отрезок прямой от до .

12. по отрезку прямой от точки до точки .

13. по отрезку прямой от точки до точки .

14. по кривой , , .

15. , если , , .

16. , где - отрезок прямой от до .

17. , где - парабола , соединяющая точки и .

18. , где - ломаная, проходящая через точки , и .

19. , если - ломаная , где , ,

20. , если - дуга полукубической параболы от до .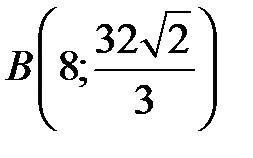

Задача 9. Проверить, что данное дифференциальное выражение есть полный дифференциал некоторой функции и затем найти u:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

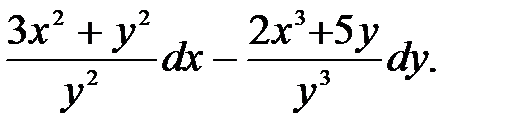
17.

18.

19.

20.