Вычисление площади посредством двойного интеграла

Площадь S плоской фигуры области D равна двойному интегралу по об­ласти D.

В прямоугольной системе координат: .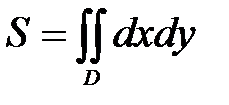

В полярных координатах: .

Пример 13. Найти площадь области, ограниченной линиями

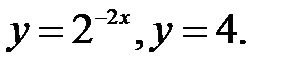
Решение. Сделаем рисунок 19, область D - это криволинейный треуголь­ник ABC. Область D будет правильная в направлении оси ОХ.

Рис. 19 Рис. 20

Пример 14. Вычислить площадь фигуры, ограниченной кривыми

Решение. Определим точки пересечения данных кривых (рис. 20). В точке пересечения ординаты равны, т.е. отсюда 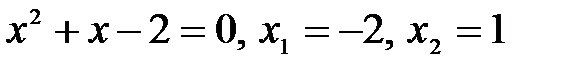. Получим две точки пересечения . Область D - правильная в направлении OУ.

Пример 15. Найти площадь области, ограниченной линиями

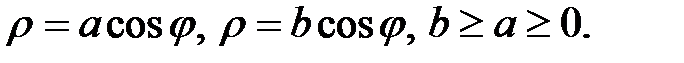
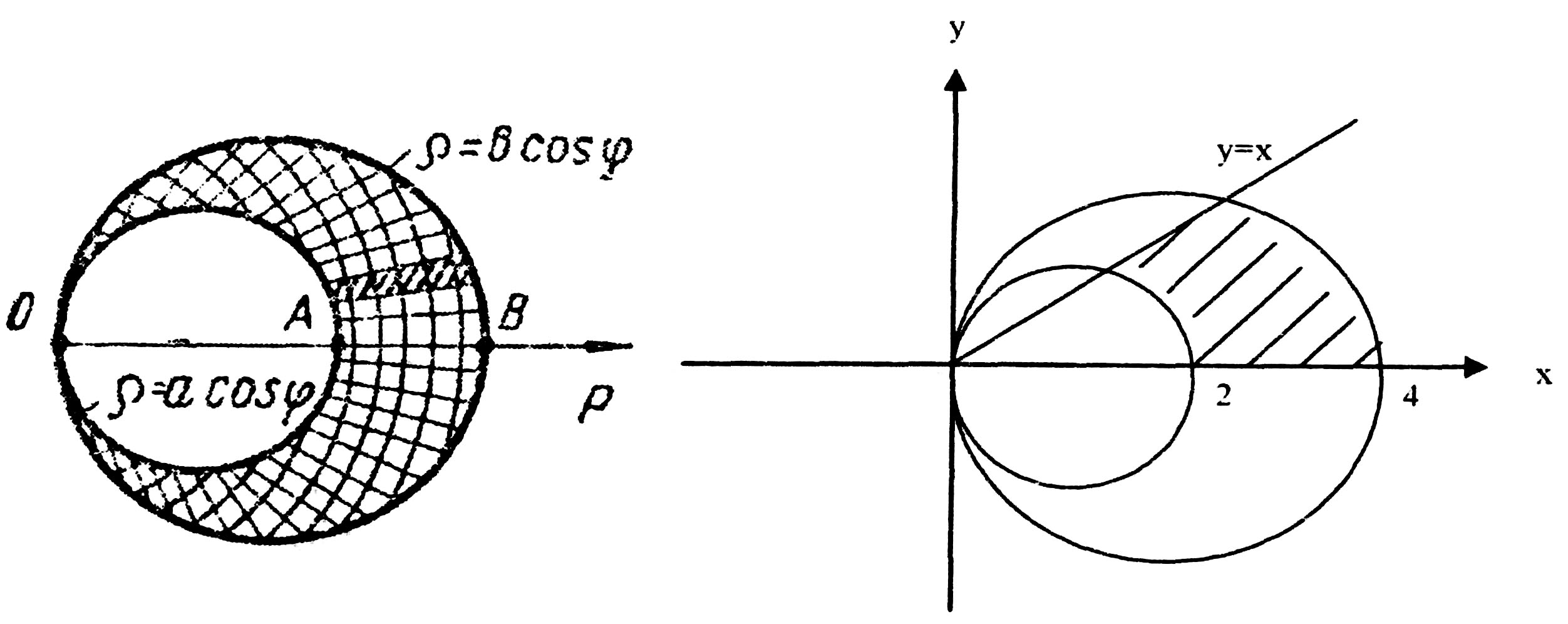
Рис. 21 Рис. 22

Решение. Построим данные окружности в полярной системе координат (рис. 21).

Пример 16. Переходя к полярным координатам, найти площадь, ограни­ченную линиями:

Решение. Уравнения окружностей приведём к каноническому виду и сделаем рис. 22,Переходя к полярной системе координат сделаем замену 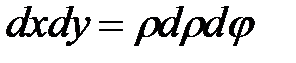. Получим т.е. отсюда следует, что от сюда следует, что

 

Вычисление объема тела посредством двойного интеграла

Объём вертикального цилиндрического тела, имеющего своим основани­ем область D на плоскости хОу и ограниченного сверху поверхностью (рис. 23),выражается двойным интегралом

Рис. 23 Рис. 24 Рис. 25

Вычисление объёмов тел более сложной формы сводится к вычислению алгебраической суммы объёмов нескольких вертикальных цилиндрических тел с образующими, параллельными оси Oz.

Пример 17. Вычислить объём тела, ограниченного поверхностями

Решение. Данное тело (рис. 24)представляет вертикальный цилиндр, ко­торый сверху ограничен частью плоскости а снизу - частью плоскости, заключённой между параболой и прямой

Пример 18. Вычислить объём тела, ограниченного поверхностями:

Решение. Гиперболический параболоид 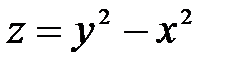пересекает плоскость хОу по двум прямым он ограничивает тело, симметричное плоско­стей xOz и yOz. Объём четвертой части тела, расположенной в первой октаве (рис. 25),равен:

 

Вычисление массы, центра тяжести и моментов инерции плоской фигуры посредством двойного интеграла

Если есть поверхностная плотность в точке 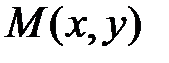плоской фигуры (материальной пластинки), занимающей область D, то её масса m, координаты центра тяжести и моменты инерции относительно осей Ох, Оу - I_x, I, и начала координат О –I₀, выражаются формулами:

1)

2) ,

где - статистически моменты пластинки относительно осей Ох, Оу.

3)

Пример 19. Найти массу кругового кольца если в каждой его точке поверхностная плотность обратно пропорциональна квадрату расстояния её до центра кольца, т.е.

Пример 19. Найти центр тяжести треугольника, ограниченного следую­щими прямыми: . Плотность р = у (рис. 26).

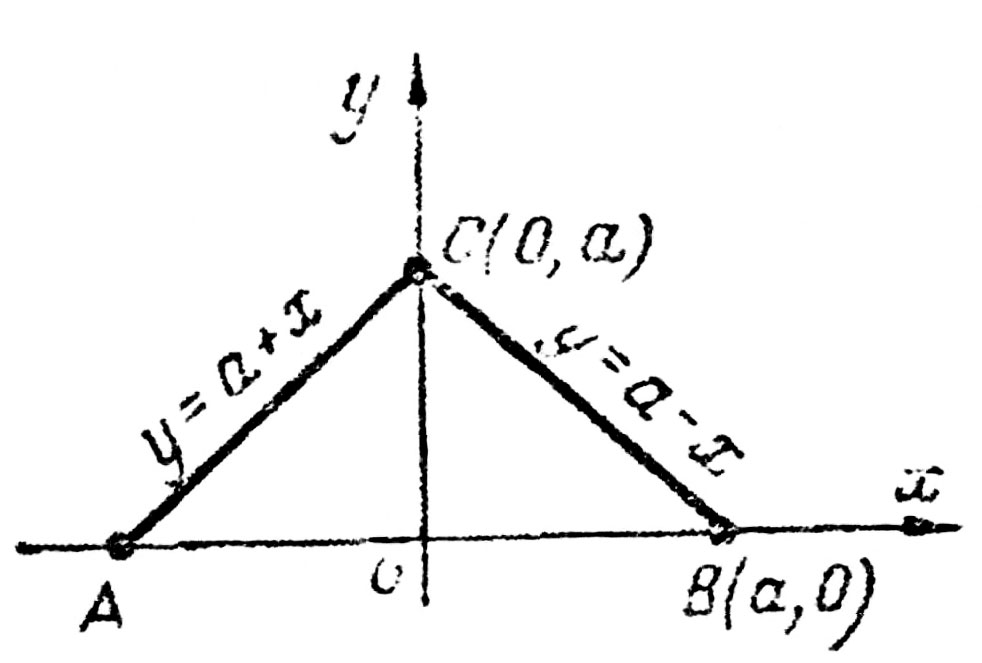
Рис. 26

Решение.

Следовательно,

Центр тяжести размещается в точке пересечения медиан:

Задача 20. Найти моменты инерции треугольника, данного в условиях предыдущей задачи.

Решение.

 

 

ТРОЙНОЙ ИНТЕГРАЛ