Надійність забезпечення необхідної точності обробки заготовок характеризується запасом точності даної операції, що визначається за формулою  ,
, 
де 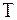 - допуск на обробку заготовок;
- допуск на обробку заготовок;  - фактичне поле розсіювання розмірів заготовок.
- фактичне поле розсіювання розмірів заготовок.
Величини поля розсіювання  при різних законах розподілу розмірів оброблюваних заготовок приводяться нижче.
при різних законах розподілу розмірів оброблюваних заготовок приводяться нижче.
Нормальний розподіл (закон Гауса).............. 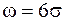 .
.
Рівнобедрений трикутник (закон Сімпсона)  .
.
Рівна ймовірність............................................  .
.
Ексцентриситет (закон Релея).........................  .
.
Обробка заготовок може бути здійснена без браку, коли запас точності  і за умови правильного налагодження верстата (поле кривої розсіювання збігається із серединою поля допуску).
і за умови правильного налагодження верстата (поле кривої розсіювання збігається із серединою поля допуску).
При  процес обробки вважається надійним. Для всіх законів розподілу розмірів умовою обробки заготовок без браку є умова
процес обробки вважається надійним. Для всіх законів розподілу розмірів умовою обробки заготовок без браку є умова  , яка показує, що поле фактичного розсіювання розмірів менше допуску на виготовлення. Для закону нормального розподілу цей вираз набуває вигляду
, яка показує, що поле фактичного розсіювання розмірів менше допуску на виготовлення. Для закону нормального розподілу цей вираз набуває вигляду  .
.
При наявності систематичної похибки  , що викликає зсув поля розсіювання розмірів, умова обробки заготовок без браку наступна:
, що викликає зсув поля розсіювання розмірів, умова обробки заготовок без браку наступна:
 . (6.1)
. (6.1)
Визначення ймовірного відсотка бракованих деталей
Тому що площа, обмежена кривою Гаусса і полем розсіювання 6s прийнята за 100% оброблених заготовок (деталей), то задача зводиться до визначення площі під кривою, займаної придатними чи бракованими обробленими заготовками (деталями).
Для зручності технологічних розрахунків рівняння кривої нормального розподілу в цьому випадку представляється не у вихідному, а в нормованому виді. Нормування розподілу полягає в переході від випадкової величини L до допоміжної величини
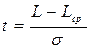
Тоді величину площі, обмежену кривою нормального розподілу і перпендикулярами, проведеними з точок L і Lср (наприклад, незаштриховані площі на рис. 6.1 праворуч і ліворуч від Lср до  , чи до
, чи до  ), можна визначити за допомогою функції Лапласа:
), можна визначити за допомогою функції Лапласа:
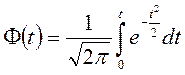 . .
| (6.2) |
На рис. 6.1 наведені різні варіанти розташування кривої розсіювання розмірів стосовно середини поля допуску. Величина Dн є похибкою налагодження верстата на заданий розмір. Незаштриховані площі під кривими є придатними обробленими заготовками (деталями), а заштриховані площі – брак. При цьому брак ліворуч від Lср (q) є поправним для отворів і непоправним для валів, а брак праворуч (q) – поправним для валів і непоправним для отворів.

Для часткового випадку (рис 6.1, а) нормований параметр розподілу: 

Для загального випадку (рис. 6.1, б) нормований параметр розподілу t може бути представлений у різних варіантах:

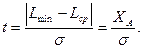
Тоді відсоток придатних заготовок (деталей) ліворуч і праворуч від Lср буде дорівнювати відповідно:
 чи чи 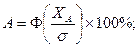
 чи чи 
| (6.3) |
Відсоток браку визначається як різниця 50% і відсотка придатних заготовок (деталей) з кожної сторони від Lср:
 чи чи 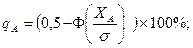
 чи чи 
| (6.4) |
У формулах 6.4: 
Розв’язок функції Лапласа залежить не від конкретних значень  і
і  , а від відношення цих параметрів.
, а від відношення цих параметрів.
Інтервал зміни параметра  від 0 до 3 практично охоплює весь діапазон можливих коливань функції Лапласа від 0 до 0,49865. По величині функції Лапласа судять про кількість придатних деталей у відсотках, наприклад,
від 0 до 3 практично охоплює весь діапазон можливих коливань функції Лапласа від 0 до 0,49865. По величині функції Лапласа судять про кількість придатних деталей у відсотках, наприклад,  відповідає 49,865% придатних деталей з 50%. У табл. додатка 1 приведені результати розрахунку функції Лапласа в інтервалі зміни аргументу
відповідає 49,865% придатних деталей з 50%. У табл. додатка 1 приведені результати розрахунку функції Лапласа в інтервалі зміни аргументу  від 0 до 5.
від 0 до 5.
Методику розрахунку кількості бракованих деталей, засновану на використанні табульованої функції Лапласа, розглянемо на конкретному прикладі.
Приклад: на токарно-револьверному верстаті, налагодженому на розмір, оброблялася партія валів  у кількості 500 штук. За результатами виміряних 75 оброблених деталей визначена емпірична величина середньоквадратичного відхилення
у кількості 500 штук. За результатами виміряних 75 оброблених деталей визначена емпірична величина середньоквадратичного відхилення  . Приймаючи, що центр групування розмірів збігається із серединою поля допуску, визначимо кількість бракованих деталей. Розрахункова схема представлена на
. Приймаючи, що центр групування розмірів збігається із серединою поля допуску, визначимо кількість бракованих деталей. Розрахункова схема представлена на
рис. 6.1, а.
Розв’язок.
1. Приймаємо, що розподіл розмірів підкоряється закону Гауса. Систематичні похибки відсутні.
2. Визначаємо розрахункове значення середнього квадратичного відхилення  за формулою
за формулою 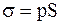 . Величина поправочного коефіцієнта
. Величина поправочного коефіцієнта  визначається з табл. 6.1.
визначається з табл. 6.1.
| Таблиця 6.1 | |||||
| nшт | DS % | p | nшт | DS % | p |
| 42,4 | 1,4 | 15,0 | 1,15 | ||
| 30,0 | 1,3 | 12,2 | 1,12 | ||
| 25,0 | 1,25 | 10,6 | 1,11 | ||
| 21,2 | 1,2 | 10,0 | 1,10 |
 .
.
3. Поле фактичного розсіювання розмірів w=6s=6×0,025=0,15 мм перевершує поле допуску  . Отже, умова роботи без браку
. Отже, умова роботи без браку  не виконується, і поява браку – неминуча.
не виконується, і поява браку – неминуча.
4. Відповідно до розрахунку
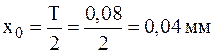 ,
,
 .
.
Отриманому аргументу відповідає функція  . Отже, кількість готових заготовок складає 44,52%. Для всієї партії від 500 штук кількість придатних деталей складе 89,04%, чи 445 штук, а число бракованих деталей буде дорівнює 55 штук, що складає 10,96% від 100%.
. Отже, кількість готових заготовок складає 44,52%. Для всієї партії від 500 штук кількість придатних деталей складе 89,04%, чи 445 штук, а число бракованих деталей буде дорівнює 55 штук, що складає 10,96% від 100%.
Приклад. На револьверному верстаті обробляється партія деталей  , яка складає 500 штук. Розрахункове значення середньоквадратичного відхилення дорівнює
, яка складає 500 штук. Розрахункове значення середньоквадратичного відхилення дорівнює 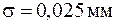 ,
, 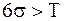 . Брак неминучий.
. Брак неминучий.
Потрібно визначити кількість придатних і бракованих деталей, якщо центр групування розмірів зміщений від середини поля допуску на величину  .
.
Розв’язок: 1. По площі  (рис. 6.1, б) визначаються значення
(рис. 6.1, б) визначаються значення  і
і  :
:
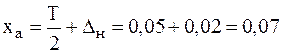 ,
,
 .
.
Визначаємо функцію Лапласа  . Кількість придатних деталей – 49,74% від 50%.
. Кількість придатних деталей – 49,74% від 50%.
2. Визначаються значення 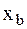 і
і  :
:
 ,
,
 .
.
 , тобто 38,49% придатних заготовок.
, тобто 38,49% придатних заготовок.
Загальна кількість придатних заготовок: 49,74+38,49 = 88,23 % чи 441 шт.
Загальна кількість бракованих деталей: 0,26 + 11,51 = 11,77 %, що складає 59 шт.






