Исследование движения материальной точки
Под действием силы тяжести в сопротивляющейся среде
В данной задаче проводится исследование движения материальной точки, находящейся под действием силы тяжести и силы сопротивления, целью которого является определение всех кинематических параметров, характеризующих это движение.
Задача относится к классу основных задач теоретической механики, и ее решение проводится на основе дифференциальных уравнений, описывающих движение материальной точки.
Решение задачи состоит из следующих операций:
1. составление дифференциальных уравнений,
2. определение начальных условий,
3. решение дифференциальных уравнений.
Составление дифференциальных уравнений.
Дифференциальные уравнения движения точки имеют вид
,
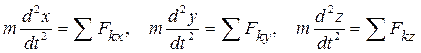где m – масса материальной точки, x, y, z – ее координаты в произвольный момент времени, Fkx, Fky, Fkz - проекции приложенных к этой точке сил на оси координат.
Поскольку правые части этих уравнений не зависят от содержания конкретной задачи, составление дифференциальных уравнений сводится к определению суммы проекций всех приложенных к точке сил на выбранные оси координат. Для того, чтобы оформить правую часть каждого дифференциального уравнения, необходимо выполнить следующие действия
1. Выбрать систему координат, начало которой следует совместить с известным по условию задачи положением точки, а оси координат направить так, чтобы координаты движущейся точки вблизи начального положения были положительными.
2. Провести анализ каждой действующей на точку силы: определить ее направление и закономерности изменения, изобразить на чертеже и определить проекции на каждую координатную ось. Сложив проекции всех сил на каждую координатную ось, получим соответствующие правые части дифференциальных уравнений.
Составим дифференциальные уравнения точки, движущейся под действием силы тяжести в сопротивляющейся среде.
Выберем неподвижную систему координат Оxyz так (рис. 1)
чтобы относительно нее было удобно определять положение движущейся точки М. Совместим начало координат с начальным положением точки, ось z направим вертикально вверх, горизонтальные оси координат Ох и Оу направим так, чтобы при небольшом отклонении точки от начального положения ее координаты х и у были положительными.
1.2. Проведем анализ действующих на точку сил. В выбранной системе координат (рис.1) изобразим материальную точку и покажем действующие на нее силу тяжести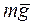 
, силу сопротивления 
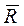и определим их проекции на выбранные оси координат.
Сила тяжести направлена вертикально вниз, поэтому ее проекции на горизонтальные оси Ох и Оу равны нулю, проекция на ось z равна 
.
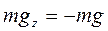Силы сопротивления появляются в том случае, когда тело движется в какой-либо среде. Так, например, на тело, движущееся в воздухе или воде, действует со стороны этих сред сила, препятствующая движению. Действующая на тело сила сопротивления всегда направлена противоположно скорости движения. Когда относительная скорость обращается в ноль, сила сопротивления исчезает. Зависимость силы сопротивления от скорости движения носит в общем случае сложный характер. Многочисленными экспериментами установлено, что при медленном движении тела в газообразной или жидкой среде силы сопротивления пропорциональны первой степени скорости.
При более высоких скоростях имеет место так называемый квадратный или гидравлический закон сопротивления.
Наконец, при очень больших скоростях движения зависимость оказывается более сложной, однако, как в предыдущих вариантах с достаточной степенью точности можно считать, что сила сопротивления зависит только от скорости и всегда направлена против скорости.
Определим проекции сил сопротивления на оси координат для первых двух случаев.
Пусть сила сопротивления прямо пропорциональна величине скорости точки. Такая сила может быть представлена в виде векторной формулы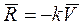 
, где k - коэффициент пропорциональности; 
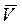- вектор скорости точки.
Проекции силы сопротивления на оси координат равны:
; 
; 
.
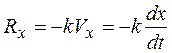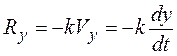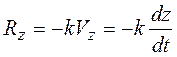Дифференциальные уравнения движения точки принимают вид
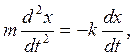
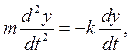
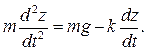
Пусть величина силы сопротивления, действующей на точку, пропорциональна квадрату скорости точки: R = kV2.. Векторы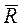 
и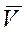 
направлены по касательной к траектории точки в противоположные стороны, единичный вектор 
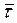- в сторону скорости движения точки.
Тогда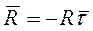 
, где R = kV2.
Значит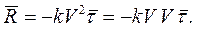 
,
Заменим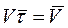 
,
Следовательно, вектор силы сопротивления равен
.
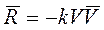Проекции этого векторного равенства на оси координат будут равны
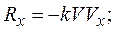
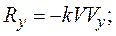
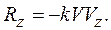
Модуль вектора скорости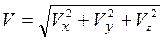 
, проекции скорости на оси координат 
.
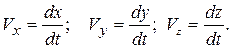Тогда, проекции силы сопротивления на оси координат будут равны
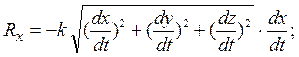
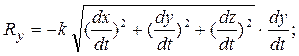
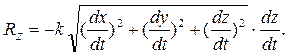
Дифференциальные уравнения в данном случае будут записаны в виде
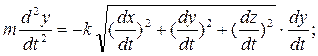
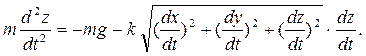
Если точка движется в вертикальной плоскости Оху, проекции силы сопротивления на оси координат будут равны
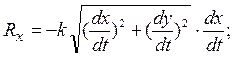
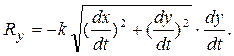
В этом случае будет два дифференциальных уравнения
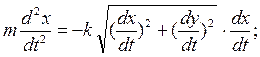
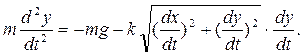
В том случае, когда начальная скорость точки направлена вертикально по оси Оу, движение точки окажется прямолинейным. Такому движению будет соответствовать одно дифференциальное уравнение
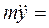
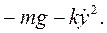
2.Определение начальных условий заключается в том, чтобыв выбранной системе координат определить координаты точки и проекции ее скорости на оси координат в начальный момент времени. Значения указанных характеристик зависят от условия задачи и выбранной системы координат. В результате необходимо записать полученные значения при t = 0: x = x0, y = y0, z = z0,
Vx=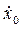 
, Vy = 
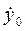, Vz = 
.
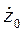Если движение точки является плоским относительно системы координат Оху, то соответствующие начальные условия должны быть записаны в виде:
t = 0: x = x0, y = y0,
Vx= 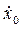, Vy = .
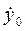3.Решение дифференциальных уравнений. В данной работе предлагается графическое решение дифференциальных уравнений, описывающих движение материальной точки на основе компьютерной программы Mathcad.
Задание Д -2.
Тело массой m движется из точки А по участку АВ = l наклонной плоскости, составляющей угол α с горизонтом, в течение τ секунд. Его начальная скорость V A, коэффициент трения скольжения тела по плоскости равен f. Силой сопротивления на данном участке пренебречь.
В точке В тело покидает плоскость со скоростью V В и падает со скоростью V С в точку С на наклонную или горизонтальную плоскость (варианты 20 – 21, 25-30) или ударяется о вертикальную плоскость(варианты 22-24), находясь в воздухе Т секунд. Положение плоскости определяется углом наклона (β или γ) или параметрами точек D и D1, через которые она проходит.
При движении в воздухе на тело действует сила сопротивления, пропорциональная скорости (варианты 1-24) или пропорциональная квадрату скорости (варианты (24-30), коэффициент пропорциональности равен k.
1. Определить все характеристики движения тела по наклонной плоскости АВ: уравнение движения, зависимость скорости и ускорения от времени, время движения по наклонной плоскости, если задана ее длина l, или ее длину, если задано время τ, значение скорости V В в точке В.
2. Принимая во внимание силу сопротивления, составить дифференциальные уравнения движения тела в воздухе, определить траекторию этого движения, построить графики зависимости скорости и ускорения от времени, определить время движения в воздухе, установить место падения тела на заданную плоскость, определив координаты точки падения, вычислить конечную скорость.
3. Определить движение тела в воздухе без учета силы сопротивления, найти траекторию, скорость и ускорение этого движения, установить место удара тела о наклонную плоскость и его скорость в этот момент.
4. Сравнить движение тела в воздухе при наличии силы сопротивления и без нее.
Варианты 1-3.
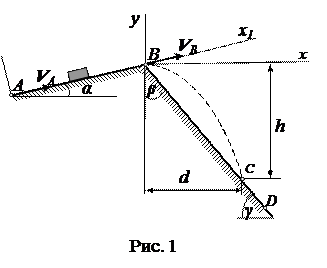Вариант 1. Дано: m = 2 кг,
α = 150; f = 0,1; VA = 25 м/c;
l = 5 м; β = 400; k =0,4.
Вариант 2. Дано: m = 0,5 кг,
α = 200; f = 0,12; VA = 20 м/c;
τ = 3 с; γ = 450; k =2.
Вариант 3. Дано: m = 3 кг,
α = 180; f = 0,1; VA = 16 м/c;
τ = 3с; xD = 60м; yD =-100м;
k =0,6.
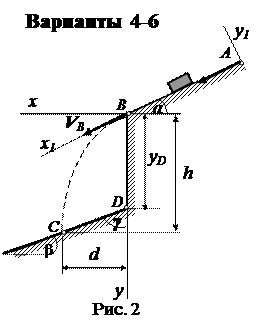
Вариант 4. Дано: m = 1,5 кг;
α=200; VA =2 м/c; f = 0,12;
τ = 5 c; γ= 750; yD=-12 м;
k =0,36.
Вариант 5. Дано: m = 2 кг;
α= 200; VA =2 м/c; f = 0,12;
τ = 3 c; β = 600; yD = - 30 м;
k =0,36;
Вариант 6. Дано: m = 1,5 кг;
α = 150; VA =5 м/c; l = 12 м;
f = 0,2; k =0,36; γ = 450;
yD =-15 м; k =0,36.
Варианты 6-9
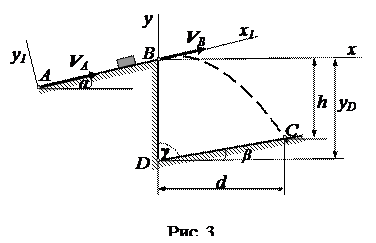Вариант 7. Дано: m = 2 кг, α = 150; VA = 20 м/c; f = 0,1; l = 5 м; k =0,4; β = 300;
yD =80 м.
Вариант 8. Дано: m = 1 кг, α = 200; f = 0,12; τ = 3 с;
VA = 28 м/c; γ = 700; k =2; yD =-74 м.
Вариант 9. Дано: m = 3 кг, α = 180;VA = 16 м/c; f = 0,1; τ = 4 с; γ =1200; yD =-20 м.
k =0,6.
Варианты 10 – 12
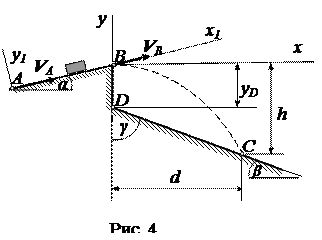Вариант 10. Дано: m = 60 кг; α = 150; VA = 18 м/c; f = 0; l = 6 м; β = 400; yD = -15 м;
k = 9.
Вариант 11. m = 60 кг;
α =120, VA = 22 м/c; f =0,2;
τ =1 с; γ =65 0; yD =- 4 м;
k = 12;
Вариант 12. Дано: m = 50 кг; α =200; VA = 20 м/c; τ = 2 с;
f = 0,2; β = 600; yD = -2,5 м; k = 12;
Варианты 13-15
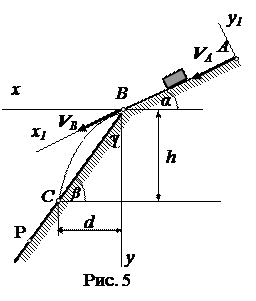Вариант 13. Дано: m = 2 кг;
α =250, VA = 4 м/c; f = 0,2;
l =10 м; β = 400; k = 0,3.
Вариант 14. Дано: m = 2 кг;
α = 180; VA = 2 м/c; f =0,2;
τ = 3 с; γ = 340; xD= 20 м;
k = 0,24.
Вариант 15. Дано: m = 2 кг;
α =150; VA = 3 м/c; τ = 2 с
f =0,18; xD =15 м; yD = 32 м;
k = 0,18.
Варианты 16-18
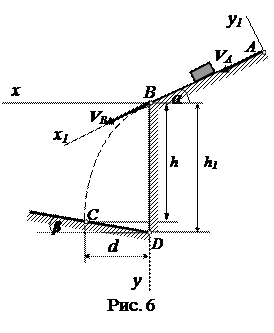Вариант 16. Дано: m = 2 кг;
α = 200; VA =2 м/c; f = 0,12;
τ = 5 c; f =0,18; β= 150;
yD=30 м; k =0,36;
Вариант 17. Дано: m = 2 кг;
α = 150; VA =3 м/c; f = 0, 2;
l = 8 м; yD = 38 м; k = 0,36;
β = 200.
Вариант 18. Дано: m = 2 кг;
α = 150; VA =3 м/c; f = 0,2;
l = 12 м; β = 400; yD =50 м;
k =0, 4.
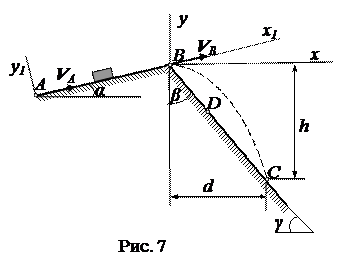Варианты 19-21 Вариант 19. Дано: m = 2 кг, α = 150; f = 0,1; VA = 25 м/c; l = 5м, м; γ = 350; k =0,4.
Вариант 20. Дано: m = 0,5 кг,
α = 200; f = 0,12; τ = 3 с;
VA = 20 м/c; k =0,2; xD = 10 м;
yD =-18 м.
Вариант 21. Дано: m = 3 кг,
α = 180; f = 0,1; VA = 16 м/c; τ = 3 с; k =0,15; γ = 400.
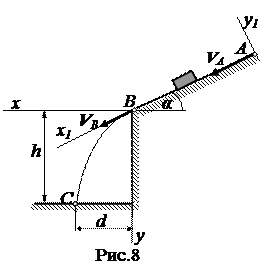Вариант 22. Дано: m = 4 кг;
α =250, VA = 12 м/c; l = 8 м;
k =0,03; h = 42 м.
Вариант 23. Дано: m = 4 кг;
α = 150; VA =3 м/c; f = 0, 2;
l = 8 м; h=38 м; k =0,36.
Вариант 24. Дано: m = 4 кг;
α = 200; VA = 3 м/c; f = 0,2;
τ = 3 c; h =40 м; k = 0, 4.
Варианты 25-27
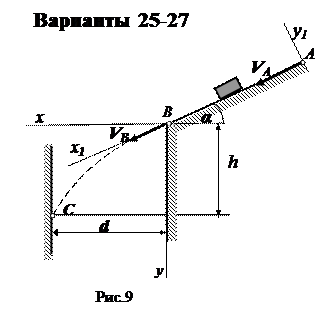Вариант 25. Дано: m =0,3 кг;
f = 0,1; α = 230; VA = 8 м/c;
τ = 5 c; d =30 м; k = 0,2.
Вариант 26. Дано: m =0,3 кг;
f = 0,12; α = 150; τ = 6 c;
VA = 10 м/c; d =24 м, k = 0,16.
Вариант 27. Дано: m =0,3 кг; f = 0,12; α = 150; VA = 12 м/c; l = 12 м; d =40 м, k = 0,18.
Варианты 28-30
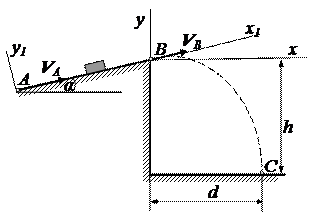Вариант 28. Дано: m = 6 кг;
α =150; f = 0,1; VA = 25 м/c;
τ= 2 сек; h = 24 м; k =0,09.
Вариант 29. Дано: m = 4 кг;
α = 200; f =0,1; VA = 25 м/c;
l =2 5 м; h = 40 м; k =0,06.
Вариант 30. Дано: m = 4 кг;
α = 200; f = 0,1; VA = 18 м/c;
l = 5 м; h = 32 м; k =0,01.
|
