Цель работы. Изучение современных методов синтеза на примере модального регулирования.
Основные теоретические положения.
Модальный регулятор является методом корневого синтеза, а именно, по желаемому расположению корней характеристического уравнения на комплексной плоскости строится модальный регулятор, который представляет собой коэффициенты отрицательной обратной связи по каждой динамической переменной.
Описание объекта представлено уравнением состояния в векторной форме:
(4.1)
Для определения возможности синтеза методом обратных связей по состоянию требуется убедиться в равенстве ранга матрицы управляемости порядку системы 
.
Матрица управляемости имеет вид
(4.2)
После этого выбирается вид желаемого характеристического полинома Dжел(p) (обычно это какая-либо стандартная форма) – в соответствии с заданными (желаемыми) показателями качества.
Матрица обратных связей для системы с одним входом имеет вид матрицы-строки, её размерность совпадает с порядком системы.
(4.3)
Для определения коэффициентов обратных связей характеристический полином системы с добавленным к ней модальным регулятором приравнивается к выбранному желаемому полиному стандартного вида.
(4.4)
Здесь: 
;
– единичная матрица.
Таким образом, получается система алгебраических уравнений, в каждом из которых коэффициент характеристического полинома системы приравнивается коэффициенту желаемого полинома при соответствующей (одинаковой) степени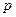 
. В результате решения уравнения (4.4), получаются численные значения коэффициентов обратных связей.
Матрицу обратных связей также можно рассчитать другим методом, используя формулу Аккермана:
(4.5)
Размерность первой матрицы-строки совпадает с порядком системы, последняя матрица определяется по формуле:
(4.6)
Здесь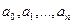 
– коэффициенты желаемого характеристического полинома.
Рис.4.1. Структурная схема системы управления с модальным регулятором.
Порядок выполнения работы.
1. Определить численные значения передаточной функции разомкнутой части исходной системы 
,
где
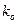= (номер варианта, умноженный на число, образованное двумя последними цифрами текущего года), плюс один;
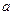= 0, если номер варианта – четный, 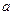= номер варианта, умноженный на 0.1, если номер варианта нечетный;
= сумма цифр номера варианта;
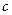= 0.5( + ).
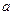2. Определить численные значения желаемых показателей качества: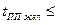 
номер варианта, умноженный на0.1;
.
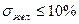3. Промоделировать переходный процесс для исходной замкнутой системы, получить основные показатели качества.
4. Построить схему переменных состояния (СПС) разомкнутого контура для нечётного варианта методом прямого программирования, для чётного – последовательного программирования.
5. Добавить единичную отрицательную обратную связь.
6. С помощью полученной СПС с добавленной обратной связью записать дифференциальные уравнения в форме Коши, получить матрицы коэффициентов A, B, C, D.
7. Убедиться в управляемости исходной САУ.
8. Получить численные значения в стандартной биноминальной форме желаемого характеристического полинома, исходя из желаемых показателей качества.
9. Рассчитать коэффициенты обратных связей по состоянию двумя способами, убедиться в совпадении результатов.
10. Промоделировать переходный процесс синтезированной САУ, получить основные показатели качества.
11. Получить численные значения в стандартной форме Баттерворта желаемого характеристического полинома, исходя из желаемых показателей качества.
12. Рассчитать коэффициенты обратных связей по состоянию двумя способами, убедиться в совпадении результатов.
13. Промоделировать переходный процесс синтезированной САУ, получить основные показатели качества.
14. Сравнить показатели качества всех рассмотренных систем в результирующей таблице, сделать вывод.
Содержание отчета.
1. На титульном листе кроме основных сведений также указывается номер варианта и номер(а) компьютера(ов), на котором(ых) проводилось моделирование.
2. Цель работы.
3. Индивидуальное задание: структурная схема, численные значения параметров.
4. Протокол выполнения работы, включая все расчеты и графики всех полученных временных характеристик, а также графики асимптотических ЛАЧХ.
