Министерство образования Российской Федерации
Пермский национальный исследовательский политехнический университет
Кафедра Микропроцессорных средств автоматизации
Теория автоматического управления
Методические указания к лабораторным работам
Пермь 2012
Составители: Андриевская Н. В., Билоус О. А.
УДК 62-5
Методические указания к лабораторным работам по курсу “Теория автоматического управления” для специальности 140211 «Электроснабжение». / Сост.: Андриевская Н. В., Билоус О. А., Пермский национальный исследовательский политехнический университет, Пермь, 2012.
Пособие представляет собой руководство к выполнению лабораторных работ по курсу “Теория автоматического управления”
Пермский национальный
исследовательский
политехнический университет
Лабораторная работа № 1.
Критерии устойчивости.
Продолжительность работы – 4 часа.
Цель работы. Изучение алгебраических критериев устойчивости Гурвица и Рауса, частотных критериев устойчивости Михайлова и Найквиста.
Краткие теоретические сведения
Исследование устойчивости систем автоматического управления является одной из важнейших задач теории автоматического управления. Известно, что устойчивость САУ может быть определена путем анализа корней характеристического уравнения системы:
(1.1)
Корни могут быть действительными, комплексными и чисто мнимыми.
Общее условие устойчивости:
Для устойчивости линейной автоматической системы управления необходимо и достаточно, чтобы действительные части всех корней характеристического уравнения системы были отрицательны.
Если хотя бы один корень имеет положительную действительную часть, то система будет неустойчивой. Используя геометрическое представление корней на комплексной плоскости (см. рис. 1.1) в виде векторов или точек, можно дать вторую формулировку общего условия устойчивости (эквивалентную основной):
Для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения находились в левой полуплоскости. Если хотя бы один корень находится в правой полуплоскости, то система будет неустойчивой.
Рис. 1.1. Расположение корней характеристического уравнения на комплексной плоскости.
Мнимая ось jb является границей устойчивости в плоскости корней. Если характеристическое уравнение имеет одну пару чисто мнимых корней (pk=+jbk, pk+1=-jbk), а все остальные корни находятся в левой полуплоскости, то в системе устанавливаются незатухающие гармонические колебания с круговой частотой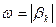 
. В этом случае говорят, что система находится на колебательной границе устойчивости.
Точка b =0 на мнимой оси соответствует так называемому нулевому корню. Если уравнение имеет один нулевой корень, то система находится на апериодической границе устойчивости. Если таких корня два, то система неустойчива.
В теории автоматического управления пользуются условиями, которые позволяют судить о расположении корней в левой полуплоскости без нахождения их значений. Эти условия называются критериями устойчивости. Критерии устойчивости бывают алгебраические и частотные.
