Критерий Михайлова так же, как критерии Гурвица и Рауса, основан на анализе характеристического уравнения системы, поэтому с его помощью можно судить об устойчивости замкнутых и разомкнутых систем.
Подставим в характеристический полином вместо переменного p чисто мнимый корень, который в дальнейшем будем обозначать jw. Тогда получим функцию комплексного переменного
(1.5)
которую можно так же, как амплитудно-фазовую характеристику, представить в виде суммы действительной и мнимой частей:
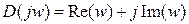(1.6)
Действительная часть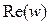 
содержит только четные степени переменного w:
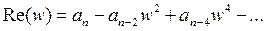(1.7)
а мнимая часть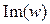 
— только нечетные:
(1.8)
Каждому фиксированному значению переменного w соответствует комплексное число, которое можно изобразить в виде вектора на комплексной плоскости. Если теперь изменять параметр w от 0 до ¥, то конец вектора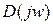 
опишет некоторую линию (рис.1.2, а), которая называется характеристической кривой или годографом Михайлова. По виду этой кривой можно судить об устойчивости системы.
Формулировка критерия Михайлова: автоматическая система управления, описываемая уравнением п-го порядка, устойчива, если при изменении w 0 до ¥ характеристический вектор системы 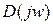повернется против часовой стрелки на угол np/2, не обращаясь при этом в нуль.
Это означает, что характеристическая кривая устойчивой системы должна при изменении w от 0 до ¥ пройти последовательно через n квадрантов. Из выражений (1.7) и (1.8) следует, что кривая 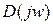всегда начинается в точке на действительной оси, удаленной от начала координат на величину an.
Рис. 1.2. Характеристические кривые.
Характеристические кривые, соответствующие устойчивым системам, имеют плавную спиралеобразную форму и уходят в бесконечность в том квадранте, номер которого равен порядку уравнения (рис.1.2, б.). Если характеристическая кривая проходит n квадрантов не последовательно или проходит меньшее число квадрантов, то система неустойчива (рис.1.2, в.). Если кривая F(jw) проходит через начало координат, то система находится на границе устойчивости. В практических расчетах удобно применять
следствие из критерия Михайлова: система устойчива, если действительная и мнимая части характеристической функции 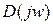обращаются в нуль поочередно, т.е. если корни уравнений 
и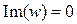 
перемежаются 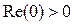и 
и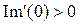 
(рис.1.2, г.).
Критерий Найквиста был сформулирован американским физиком X. Найквистом в 1932 г.
Критерий Найквиста позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой характеристике разомкнутого контура системы.
Формулировка критерия Найквиста: замкнутая автоматическая система управления устойчива, если разность между числом положительных (сверху вниз) и отрицательных (снизу вверх) переходов АФЧХ через ось абсцисс слева от точки (-1; ј 0) равна m/2, где m — число правых корней характеристического уравнения разомкнутого контура.
Если АФЧХ начинается или заканчивается на отрезке (-∞; -1), то считают, что характеристика совершает полперехода.
Для использования изложенного приема применительно к астатическим системам, которые содержат интегрирующие звенья, и амплитудно-фазовые характеристики которых начинаются в -∞, характеристику W(јω) предварительно дополняют дугой окружности бесконечно большого радиуса, длина дуги зависит от порядка астатизма. Для определения устойчивости систем с астатизмом порядка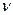 
, следует дополнить АФЧХ разомкнутой системы дугой 
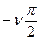окружности бесконечно большого радиуса и затем применить критерий Найквиста.
Частота, при которой амплитудная характеристика А(ω) принимает значение 1, называется частотой среза и обозначается ωср. Частоту, при которой фазовый сдвиг
φ(ω) = -π, обозначают ωπ.
Пользуясь введенными обозначениями, можно записать условие нахождения системы на границе устойчивости:
(1.9)
Частота, с которой система колеблется на границе устойчивости, называется критической и обозначается ωкр.
Порядок выполнения работы.
1. Получить индивидуальное задание – линейную непрерывную систему третьего порядка.
2. Подобрать параметры исследуемой САУ:
2.1. Получить характеристическое уравнение системы, подставить числовые значения.
2.2. Выписать условия устойчивости по критерию Гурвица, получить зависимость Ki(Tj).
2.3. Задаться значениями Ki и Tj, при которых САУ будет устойчива.
2.4. Подставить параметры для устойчивого состояния в характеристическое уравнение. Найти корни получившегося уравнения.
2.5. Собрать схему для моделирования устойчивого переходного процесса САУ (схема системы_1).
2.6. Добавить в разомкнутый контур звено запаздывания, подобрать путем моделирования величину запаздывания так, чтобы система осталась устойчивой (схема системы_2).
3. Исследовать устойчивость системы со звеном запаздывания с помощью критерия Михайлова:
3.1. Получить действительную -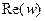 
и мнимую - 
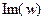составляющие характеристической функции 
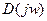для системы_2.
3.2. Построить годограф Михайлова, убедиться в устойчивости системы по виду годографа.
4. Исследовать устойчивость системы со звеном запаздывания с помощью критерия Найквиста:
4.1. Определить устойчивость разомкнутой системы_1 (третьего порядка) любым критерием (найти количество правых корней).
4.2. По виду АФЧХ разомкнутой системы_2 (со звеном запаздывания) определить устойчивость замкнутой системы_2.
5. Исследовать устойчивость системы со звеном запаздывания, используя алгебраические критерии:
5.1. Заменить в разомкнутом контуре звено запаздывания апериодическим, подобрать путем моделирования величину постоянной времени этого звена так, чтобы вид переходного процесса был приближен к результату п.2.6. (схема системы_3).
5.2. Получить характеристическое уравнение системы_3, подставив числовые значения.
5.3. Доказать устойчивость системы_3 критерием Гурвица.
5.4. Доказать устойчивость системы_3 критерием Рауса.
5.5. Доказать устойчивость системы_3 аналитически, используя критерий Михайлова (следствие).
Содержание отчета
1. На титульном листе кроме основных сведений также указывается номер варианта и номер(а) компьютера(ов), на котором(ых) проводилось моделирование.
2. Цель работы.
3. Индивидуальное задание: структурная схема, численные значения параметров.
4. Протокол выполнения работы, включая графики всех полученных характеристик и все расчеты и преобразования для схем.
