Решение типовой задачи на построение однофакторной группировки, расчёт эмпирических (табличных) показателей силы и тесноты связи. Оценка полученных результатов. Построение теоретической и эмпирической линий регрессии. Самостоятельное выполнение контрольного задания на аналитический расчет параметров регрессии и корреляционный анализ.
При решении задач на эту тему необходимо иметь четкое понятие о статистической закономерности, которая только в массе наблюдений проявляется как закон, а в каждом отдельном случае связана со случайностью. Следует учитывать особенности, отличающие статистические зависимости от функциональных, и методы их изучения.
Основной принцип анализа – это сопоставление изменения признака-фактора с вариацией групповой средней признака-результата. Если последняя не изменяется от группы к группе, то делается вывод об отсутствии связи между фактором (x) и результатом (y). Такие характеристики связи, как направление связи (прямая или обратная) и форма связи (линейная и нелинейная) выявляются на основе графического изображения множества точек на плоскости корреляции. Координаты точек: по оси x – значение фактора, по оси y – значение результата. На основании данных групповых средних фактора и результата аналитической группировки изображается эмпирическая линия регрессии.
Пример анализа парной регрессии. Имеются данные о фондоотдаче предприятия (табл. 6.1).
Таблица 6.1
| Годы | Фондоотдача | Расчетные графы | Теоретическое
значение
| |||
| Активная часть фондов (ОПФ) у.д.е. | Объём выпуска продукции (ОВП) у.д.е. | х² | ху | |||
| 2,26 | 1,12 | 5,11 | 2,53 | 1,04 | ||
| 2,06 | 1,06 | 4,24 | 2,18 | 0,99 | ||
| 1,71 | 0,92 | 2,92 | 1,57 | 0,92 | ||
| 1,67 | 0,88 | 2,79 | 1,47 | 0,91 | ||
| 1,52 | 0,74 | 2,71 | 1,28 | 0,87 | ||
| ∑ | 9,22 | 4,72 | 17,37 | 9,03 | 4,73 |
Подставим данные в систему нормальных уравнений:
4,72 = 5 а + 9,22 b
9,03 = 9,22 а + 17,37 b.
Решив систему, получим:
а = 0,54
b = 0,22
Уравнение регрессии имеет вид:
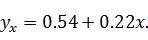
Подставив эмпирические значения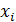 
вполученное уравнение, заполняем последний столбец.
Для расчета величины связи по данным примера составляется дополнительная таблица:
Таблица 6.2
| Годы | 
| 
| 
| 
| 
| 
|
|
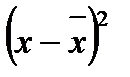
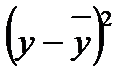
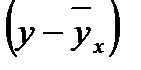
| 0,42 | 0,176 | 0,18 | 0,0324 | 0,08 | 0,0064 | 0,0756 | |
| 0,22 | 0,0484 | 0,12 | 0,0144 | 0,07 | 0,0049 | 0,0264 | |
| … | |||||||
| -0,32 | 0,1024 | -0,10 | 0,010 | -0,03 | 0,0009 | 0,0320 | |
| 0,373 | 0,0608 | 0,0131 | 0,1462 |
Учитывая, что
рассчитываются:
1) коэффициент линейной корреляции:
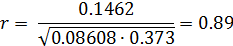
2) индекс корреляции:
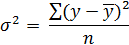
s² = 0.0608 / 5 = 0.01216
sx² = 0.0131 / 5 = 0.0026
= 0.89
3) корреляционное отношение:
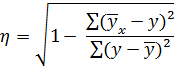
4) коэффициент детерминации:
Так как r = R = 
можно считать, что гипотеза о линейной форме связи подтверждена.
Коэффициент эластичности (Э ) для линейной парной корреляции определяется по формуле:
Для рассматриваемого примера:
Т. е. при изменении фондов на 1 ед. своего измерения, объем выпуска продукции увеличится на 0.43 ед. того же измерения.
При решении индивидуальной задачи необходимо по исходным данным построить однофакторную группировку с оптимальным числом групп, рассчитать показатели тесноты и силы связи, дать графическую иллюстрацию выявленной связи. Проанализировать полученные результаты и оформить их в краткой аналитической записке.
Практическое занятие № 7
