1. Вычислите рациональным способом
2. Найдите значение выражений:
3. Найдите область определения выражений:
4. Решите уравнение (9 · x + 37): 8 = 8 на основе зависимости между компонентами и результатом действий.
5. Представьте уравнение (x – 4,5) · (2x + 7) (4x – 1) = 0 в виде дизъюнкции и найдите его множество решений.
6. Решите неравенство 
, объясняя где и какой теоремой о равносильных неравенствах пользовались.
7. Дана теорема: «В параллелограмме противоположные углы равны». Сформулируйте для нее обратное, противоположное, обратное противоположному предложения. Являются ли они теоремами?
8. Сформулируйте утверждение «Если число натуральное, то оно целое» различными способами.
9. Сформулируйте отрицания высказываний:
а) Число 7 – дробное;
б) В любом треугольнике сумма внутренних углов равна 180°;
в) Число 35 кратно 5 и 7.
10. Составьте таблицу истинности для высказывания 
.
11. Найдите множество истинности предиката 
при условии, что 
12. На множестве X={0,1,2,3,4,5,6,7,8,9,10,11,12} даны предикаты 
Найдите множество истинности предикатов 
13. Проверьте, равносильны ли высказывания 
14. Дано множество числовых выражений A={72-5; 19+8; 48:6; 37·2}, на котором задано отношение R: "значение выражения x не больше значения выражения y". Постройте граф отношения R, укажите свойства отношения R.
15. Даны множества 
Укажите характеристическое свойство элементов множества:
16. Изобразите на координатной плоскости множество AxB, если:
17. Составьте все подмножества множества X={1,3,5,8}.
18. Даны множества: А – множество параллелограммов, В - множество ромбов, С - множество прямоугольников. Изобразите при помощи кругов Эйлера отношения между данными множествами.
19. Постройте график функции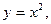 
если ее область определения X такова: а) Х=[-2; 2], б) Х={-2, -1,0,1,2}.
20. Используя соответствующие определения, покажите, что: 
21. Используя соответствующие определения, покажите, что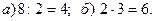 
22. Вместо звездочки поставьте такую цифру, чтобы числа 
делились на: 
23. Найдите НОД и НОК чисел, представив их в каноническом виде: а)72 и 108; б)536 и1024.
24. Решите задачу: «Зал и коридор имеют одинаковую длину. Площадь зала равна 300м2, а площадь коридора -120м2. Чему равна ширина коридора, если ширина зала равна 10м, а зал и коридор имеют форму прямоугольника».
25. Вычислить: а) 253т 92кг: 23 – 9т 345кг; б) 4мин 7с · 15 +1мин 15с · 8.
26. Известно, что 
истинное неравенство. Поставьте вместо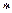 
знак > или < так, чтобы получилось истинное неравенство:
27. Сравнить числа: а) 210123 и 211003; б) 2103 и 3445.
28. Известно, что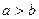 
истинное неравенство. Поставьте вместо 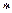знак > или < так, чтобы получилось истинное неравенство:
В О П Р О С Ы
для государственной аттестации по методике
Преподавания математики
1. Методика обучения алгоритмам умножения и деления на двузначное и трехзначное число.
2. Методика изучения основных приемов сложения и вычитания в пределах 10. Переместительное свойство сложения.
3. Характеристика основных этапов работы над задачей. Памятка.
4. Методика обучения решению простых задач, раскрывающих связь между компонентами и результатами действий умножения и деления.
5. Методика изучения понятия «Длина».
6. Цели, задачи, краткая характеристика изучения умножения и деления многозначных чисел.
7. Методические особенности изучения сложения и вычитания многозначных чисел.
8. Методика обучения решению задач, раскрывающих связь между компонентами и результатами действий сложения и вычитания.
9. Умножение и деление многозначных чисел, оканчивающихся нулями. Методика изучения свойств умножения и деления.
10. Методика сложения и вычитания однозначных чисел с переходом в разряд десятков.
11. Обучение младших школьников устным и письменным приемам умножения и деления на однозначное число в концентре «Многозначные числа».
12. Методика обучения решению задач на пропорциональное деление.
13. Изучения деления с остатком. Алгоритм деления двузначного числа на однозначное.
14. Знакомство с составной задачей. Методика обучения решению составных задач в 1 классе.
15. Методика обучения решению простых задач, раскрывающихся конкретный смысл действий умножения и деления.
16. Изучение простых задач, раскрывающих понятие кратного отношения.
17. Методика изучения задач на нахождение четвертого пропорционального.
18. Цель, задачи, характеристика приемов сложения и вычитания в пределах от 21 до 100. Работа с памятками.
19. Особенности изучения нумерации чисел в концентрах «Тысяча» и «Многозначные числа». Понятие класса.
20. Методика изучения до табличного умножения и деления. Терминология и обозначения. Знакомство с переместительным свойством умножения.
21. Методика обучения решению задач на нахождение неизвестного по двум разностям.
22. Методика изучения табличного умножения и деления. Получение каждой таблицы и обобщенная таблица умножения.
23. Изучение нумерации чисел в пределах 10. Роль наглядности при знакомстве с числами от 1 до 10.
24. Цели, задачи, характеристика содержания изучения геометрического материала.
25. Методика изучения понятия «площади».
26. Методика изучения долей и дробей в начальной школе.
27. Методика изучения «массы».
28. Изучение нумерации чисел в пределах 100. Работа с абаком.
