Когда моделируем тенденцию, то период должен быть однородным, кризисных точек не д.б., иначе временной ряд необходимо разбивать на несколько периодов и для каждого строить отдельно. Для выравнивания не стоит использовать степенную функцию (даже параболу), лучше линейную.
Метод аналитического сглаживания для выявления тенденции в рядах динамики применим только для качественно однородных периодов. Если ряд содержит структурные изменения, то выявлять тенденцию следует по подпериодам: до t* и после t*.
Для оценки возможности построения тренда по данным всего ряда без разбиения на подпериоды используется тест Чоу. Выдвигается гипотеза о том, что вектор оценок параметров (т.е. оценки всех параметров) тренда по первому подпериоду равен вектору по второму подпериоду, также о равенстве остаточных дисперсий отклонений от линий трендов по этим подпериодам: Н0: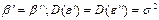 
.
Тест Чоу: 
, где р – число параметров без свободного члена, 
- остаточная сумма квадратов при построении тренда по всей совокупности, 
, 
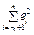- остаточные суммы квадратов для первого и второго подпериодов.
Выбор формы тренда можно осуществить с помощью теста на различие в остаточных дисперсиях: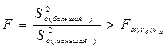 
.
Критическое значение находят при выбранном уровне значимости (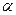
) и числе степеней свободы для большей (
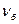) и меньшей (
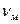) из двух дисперсий.
В случае выполнения неравенства делается заключение о том, что различия в дисперсиях существенны и функция, которой соответствует меньшая дисперсия, действительно лучше аппроксимирует исходные значения, и именно она выбирается для описания тенденции. Иначе, предпочтение отдается более простой функции.
Средняя ошибка прогноза линейного тренда рассчитывается по формуле: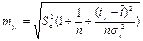 
.
Изучение взаимосвязи экономических переменных по данным временных рядов осложнено тем, что в этих рядах может быть тенденция. Чтобы выявить причинно-следственную зависимость между переменными, необходимо устранить ложную корреляцию между ними, вызванную наличием тенденции (т.к. формирование 
будет обуславливаться связями между переменными).
Существует несколько способов исключения тенденции в рядах динамики:
1.Добавление фактора времени в модель (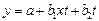
)
2.Д/каждого из временных рядов строят тренды, находят отклонения от трендов.
3.Находят первые разности и изучают зависимость ∆y=f(∆x)
Однако при моделировании временных рядов встречаются ситуации, когда имеется цикличность или сезонна компонента. Избавиться от цикличности можно выделив цикл.
