Нелинейные модели (функции спроса и предложения, степенная зависимость и т.д.) могут быть нелинейными по параметрам(парабола, можно легко привести к линейной) и по переменным.
Производственной функцией называется экономико-математическая модель, с помощью которой можно охарактеризовать зависимость результатов производственной деятельности предприятия, отрасли или национальной экономики в целом от повлиявших на эти результаты факторов.
Основными разновидностями однофакторных производственных функций являются:
1) линейная однофакторная производственная функция вида: y= 
,
2) параболическая однофакторная производственная функция вида: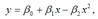 
;при условиях β0 ›0, β1 ›0, β2 ›0. Данная функция характеризуется тем, что при росте затрат ресурса х, объём произведённой продукции у вначале возрастает до некоторой максимальной величины, а затем снижается до нуля;
3) степенная однофакторная производственная функция вида: 
; при условиях β0 ›0, β1 ›0. Данная функция характеризуется тем, что с ростом затрат ресурса х, объём производства у возрастает без ограничений;
4) показательная однофакторная производственная функция вида: 
; при условиях 0‹ β1 ‹0. Данная функция характеризуется тем, что с ростом затрат ресурса х объём произведённой продукции у также растёт, стремясь при этом к значению параметра β0.
5) гиперболическая однофакторная производственная функция вида: 
Данная функция практически не применяется при изучении зависимости объёма производства от затрат какого-либо ресурса, потому что нет необходимости в изучении ресурсов, увеличение которых приводит к уменьшению объёма производства.
Двухфакторные производственные функции (с двумя факторными переменными) характеризуют зависимость объёма производства от каких-либо двух факторов, чаще от факторов объёма основного капитала и трудовых ресурсов. Чаще всего используются такие двухфакторные производственные функции как функции Кобба-Дугласа и Солоу. Функция Кобба-Дугласа 
, где у- объем производства, К-затраты капитала,L-затраты труда.
Производственная функция Кобба-Д. используются, чтобы определить, как заменить живой труд на овеществленный.
Для наглядного изображения двухфакторных производственных функций строят графики, которые называются изоквантами.
39.Системы эконометрических уравнений: виды, оценка параметров, области применения на практике.
Для описания реальных экономических систем, где статистические показатели находятся во взаимодействии и взаимосвязи, возникают сложности со спецификацией модели, поскольку многие факторные и результативные признаки взаимодействуют друг с другом. Из-за этого возникает проблема мультиколлинеарности факторов в уравнениях множественной регрессии. Одна и та же переменная может рассматриваться как факторная, независимая, а с другой – как результативная, случайная величина. Случайные переменные называют эндогенными, т.е. внутренними (y). Признаки заданные, известные, неслучайные - это экзогенные, или внешние для данной системы(x). Один и тот же признак может быть эндогенным в одной задаче и экзогенным – в другой.
В зависимости от характера взаимосвязей между эндогенными и экзогенными переменными выделяют: системы рекурсивных (рекуррентных) и совместных, одновременных, взаимосвязанных уравнений. Отличие между ними заключается в том, что в системе совместных уравнений одни и те же признаки одновременно могут выступать и в роли зависимых и в роли независимых переменных. Т.е. зависимые переменные входят в одних уравнениях в левую часть, в других – в правую часть системы:
В эконометрике такая система уравнений называется также структурной формой модели.
Структурная форма модели содержит при эндогенных переменных коэффициенты 
, экзогенных переменных –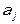 
, которые называются структурными коэффициентами модели. Все переменные в модели выражены в отклонениях от среднего уровня. В общем виде модель системы рекурсивных уравнений будет иметь вид:
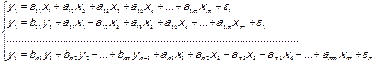
В системе рекурсивных уравнений хоты бы одна эндогенная переменная должна определятся только лишь набором независимых переменных. Если все эндогенные переменные расположены в левой части, а экзогенные – в левой, то такая система называется системой независимых уравнений. Для решения систем независимых и рекурсивных уравнений используется метод наименьших квадратов (МНК).
Косвенный МНК ( позволяет получать состоятельные и несмещенные оценки параметров структурной формы системы одновременных уравнений). Препятствие к применению МНК, которое заключается в коррелированности эндогенных переменных со случайными членами легко преодолеть, если:
1.привести систему к виду, чтобы в правой части оставались только экзогенные переменные. Такая форма называется приведенной;
2.затем применить МНК к каждому ур-ю в приведенной форме и получить оценки ее параметров;
3. перейти от приведенной формы к структурной, проведя процедуру обратного преобразования параметров.
Эта методика получила название косвенного МНК.
