Рассмотрим применение метода аналитического выравнивания по прямой для выражения основной тенденции на примере.
Уравнение прямой при аналитическом выравнивании ряда динамики имеет следующий вид:
где 
- выровненный (средний) уровень динамического ряда;
a 0, a 1 - параметры искомой прямой;
t - условное обозначение времени.
Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров a 0 и a 1:
где у - исходный уровень ряда динамики;
n - число членов ряда.
Система уравнений упрощается, если значения t подобрать так, чтобы их сумма равнялась нулю, т. е. начало времени перенести в середину рассматриваемого периода.
Если 
то
Исследование динамики социально-экономических явлений и установление основной тенденции развития дают основание для прогнозирования (экстраполяции) - определения будущих размеров уровня экономического явления.
Используют следующие методы экстраполяции:
■ средний абсолютный прирост;
■ средний темп роста;
■ экстраполяцию на основе выравнивания по какой-либо аналитической формуле.
Таблица
Исходные и расчетные данные определения параметров уравнения прямой
Расчет необходимых значений дан в таблице примера. По итоговым данным определяем параметры уравнения:
Уравнение прямой будет иметь вид:
Подставляя в уравнение принятые обозначения t, вычислим выровненные уровни ряда динамики (см. значения 
в таблице).
На основе данных таблицы рассчитаем показатели колеблемости динамических рядов, которые характеризуются средним квадратическим отклонением и коэффициентом вариации.
Среднее квадратическое отклонение можно измерить по формуле:
Используя данные нашего примера, рассчитаем показатель колеблемости урожайности зерновых культур за анализируемый период:
Коэффициент вариации исчисляется по формуле:
В нашем примере:
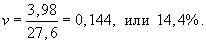
Расчет индекса сезонности
Покажем расчет индекса сезонности на примере.
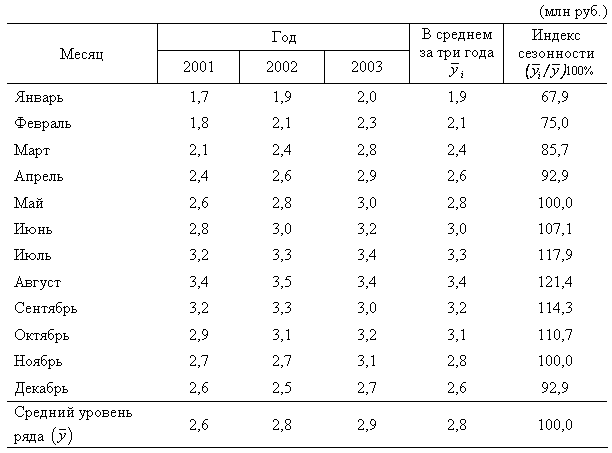
Таблица
Данные по строительной фирме об объеме выполненных работ по месяцам 2001–2003 гг. по сметной стоимости.
Для получения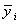 
проведем осреднение уровней одноименных периодов по формуле простой средней арифметической:
январь — 
февраль — 
…
декабрь — 
Осредненные значения уровней ряда 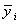для каждого месяца годового цикла представлены в таблице данного примера.
Далее по исчисленным месячным средним уровням 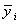определяем общий средний уровень 
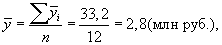
где n — число месяцев.
Значение общего среднего уровня можно вычислить также по итоговым данным за отдельные годы:
где n — число лет;
— сумма среднегодовых уровней ряда динамики.
В завершение определим индексы сезонности по месяцам года по формуле:
январь — 
февраль — 
Рассчитанные индексы сезонности представлены в таблице примера.
Следовательно, минимальный объем выполненных работ строительная фирма имела в январе, а максимальный — в августе.
Для ряда внутригодовой динамики, в которой основная тенденция роста незначительна, изучение сезонности основано на методе постоянной средней, являющейся средней из всех рассматриваемых уровней. Самый простой способ заключается в следующем: для каждого года рассчитывается средний уровень, а затем с ним сопоставляется (в процентах) уровень каждого месяца.
Однако помесячные данные одного года из-за элемента случайности могут быть ненадежными для выявления закономерности колебаний. Поэтому на практике используются помесячные данные за ряд лет (обычно не менее трех лет). Тогда для каждого месяца рассчитывается средняя величина уровня за три года, затем определяются среднемесячный уровень для всего ряда и отношение средних для каждого месяца к общему среднемесячному уровню ряда (в процентах).
Таблица1
Данные о реализации овощной продукции на городском рынке
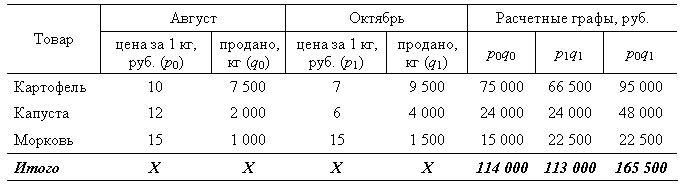
1) Цены разных товаров, реализуемых в розничной торговле, складывать неправомерно, однако с эк. точки зрения допустимо суммировать их товарооборот. Если сравнивать товарооборот в текущем периоде с его величиной в базисном периоде, то получим сводный индекс товарооборота:
Рассчитаем индекс товарооборота для примера 2.1:
| 0,9912 или 99,12% |
Мы получим, что товарооборот в целом по рассматриваемой товарной группе в текущем периоде по сравнению с базисным уменьшился на 0,88% (100-99,12).
2) На величину данного индекса оказывает влияние как изменение цен на товары, так и изменение объемов их реализации. Для того чтобы оценить изменение только цен (индексируемой величины), необходимо количество проданных товаров (веса индекса) зафиксировать на каком-либо постоянном уровне. При исследовании динамики таких качественных показателей, как цена, себестоимость, производительность труда, количественный показатель обычно фиксируют на уровне текущего уровня. Т.о. получают сводный индекс цен:
Числитель данного индекса содержит фактический товарооборот текущего периода. Знаменатель же представляет собой условную величину, показывающую, каким был бы товарооборот в текущем периоде при условии сохранения цен на базисном уровне. Поэтому соотношение этих двух категорий и отражает изменение цен. Изменение же количества реализованной продукции не влияет на величину индекса.
Вычислим сводный индекс цен для примера 1:
| 0,6828 или 68,28 % |
Следовательно, по данной товарной группе цены в октябре по сравнению с августом снизились на 31,72% (68,28-100=-31,72)
Числитель и знаменатель сводного индекса цен можно интерпретировать с точки зрения потребителей. Числитель представляет собой сумму денег, фактически уплаченных покупателями за приобретенные в текущем периоде товары. Знаменатель же показывает, какую сумму покупатели заплатили бы за те же товары, если бы цены не изменились.
Разность числителя и знаменателя будет отражать:
величину экономии (если знак «-») или
перерасхода (если знак «+») покупателей от изменения цен:
3) Третьим индексом в данной индексной системе является сводный индекс физического объема реализации. Он характеризует изменение количества проданных товаров не в денежных, а в физических единицах измерения:
Весами в данном индексе выступают цены, которые фиксируются на базисном уровне.
Индекс физического объема реализации в примере 1 составит:
| 1,4518 или 145,18% |
Физический объем реализации в октябре по сравнению с августом увеличился в 1,45 раза, или на 51 500 руб. (165 500 - 114 000).
Между рассчитанными индексами существует следующая взаимосвязь: Ip × Iq = Ipq.
Используя взаимосвязь индексов, проверим правильность вычислений:
Ipq = Ip × Iq = 0,6828 × 1,4518 = 0,9912, или 99,12%.
Следовательно, снижение товарооборота (на 0,88%) обусловлено: 1) ростом объема проданной продукции (на 45,18%) и 2) снижением цен (на 31,72%), что в абсолютном выражении составило -1000 руб. (-52 500 + 51 500).
Мы рассмотрели применение агрегатных индексов в анализе товарооборота цен и физического объема реализации. При анализе результатов производственной деятельности промышленного предприятия приведенные сводные индексы соответственно называются: - индексом стоимости продукции, -индексом оптовых цен и - индексом физического объема продукции.
Таблица
Данные о реализации овощной продукции предприятия розничной торговли округа
В примере 1 известен розничный товарооборот базисного периода, но отсутствуют данные о товарообороте текущего периода; кроме того, известно изменение физического объема реализации в текущем периоде по сравнению с базисным. В таком случае среднеарифметический индекс физического объема реализации овощной продукции можно рассчитать по следующей формуле:
Так как iqq 0 = q 1, формула этого индекса преобразуется в формулу:
Индивидуальные индексы физического объема для примера 1 равны:
iq морковь- 0,935;
iq Свекла - 0,920;
iq Лук - 1,015.
Физический объем реализации данных товаров в среднем снизился на 3,6%.
