Практическое занятие по теме
«ПОКАЗАТЕЛИ ВАРИАЦИИ»
Пример. Произведем вычисление всех показателей вариации по данным таблицы 1.
Таблица 1
Распределение кип шерсти при отгрузке
| Масса одной кипы (х), кг | Количество отгруженных кип (f), шт |
| ИТОГО |
1. Размах вариации (R) - это разность между наибольшим (х max) и наименьшим (х min) значениями вариантов: R = х max - х min = 110 – 86 = 24 кг.
Для расчета остальных показателей построим расчетную таблицу 2.
Таблица 2
Данные для расчета показателей вариации
| Масса одной кипы (х), кг | Кол.-во отгруженных кип (f), шт | хf, кг | Х- 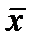 а а
| Х- 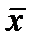 аf аf
| (х- 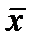 аf)*f аf)*f
| (Х- 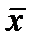 а)2 а)2
| (Х- 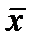 аf)2 аf)2
| (Х- 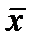 аf)2*f аf)2*f
|
| -10 | - 10,3 | 106,09 | 1060,9 | |||||
| -6 | -6,3 | 39,69 | 793,8 | |||||
| -2 | -2,3 | 5,29 | 52,9 | |||||
| -0,3 | 0,09 | 2,7 | ||||||
| +4 | +3,7 | 55,5 | 13,69 | 205,35 | ||||
| +14 | +13,7 | 205,5 | 187,69 | 2815,35 | ||||
| ИТОГО | |36| | |36,6| | - |
2. Среднее линейное отклонение определяется как средняя арифметическая отклонений индивидуальных значений от средней без учета знака этих отклонений, но сначала найдем средние (простую и взвешенную):
А) средняя арифметическая простая
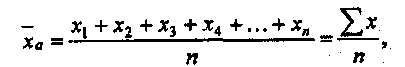
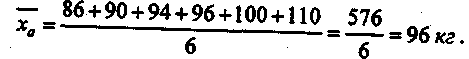
Б) средняя арифметическая взвешенное

А) Среднее линейное отклонение простое  = 36 / 6 = + 6 кг
= 36 / 6 = + 6 кг
Если данные наблюдения представлены в виде дискретного ряда распределения с частотами, среднее линейное отклонение исчисляется по формуле средней арифметической взвешенной:
Б) Среднее линейное отклонение взвешенно  = 522 / 100 = + 5,22 кг
= 522 / 100 = + 5,22 кг
3. Дисперсия ¾ это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. Дисперсия обычно называется средним квадратом отклонений и обозначается s2. В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной:
А) дисперсия простая–
 = 352 / 6 = + 58,67 кг
= 352 / 6 = + 58,67 кг
Б) дисперсия взвешенная
 = 4931 / 100 = + 49,31 кг
= 4931 / 100 = + 49,31 кг
4. Среднее квадратическое отклонение ¾ это обобщающая характеристика абсолютных размеров вариации признака в совокупности. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т. д.). Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и обозначается s:
А) среднее квадратическое отклонение невзвешенное;
 = + 7,66 кг
= + 7,66 кг
Б) среднее квадратическое отклонение взвешенное
 = + 7,02кг.
= + 7,02кг.
Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает всю представляемую совокупность.
Показатели относительного рассеивания
Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Показатель меры относительного рассеивания рассчитывается как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.
5.1. Коэффициент осцилляции (К о) отражает относительную колеблемость крайних значений признака вокруг средней:

А) простое - Ко = 24 / 96 * 100% = 25%
Б) взвешенное – Ко = 24 / 96,3 * 100% = 24,92 %
5.2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины:

А) К = 6 / 96 * 100% = 6,25%
Б) К = 5,22 / 96,3 * 100% = 5,42%
5.3. Коэффициент вариации (V). Поскольку среднеквадратическое отклонение дает обобщающую характеристику колеблемости всех вариантов совокупности, коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин. Исходят из того, что если V больше 40%, то это говорит о большой колеблемости признака в изучаемой совокупности
 .
.
А) V = 7,66 / 96 * 100% = 7,98 %
Б) V= 7,02 / 96,3 * 100% = 7,29%
.






