а). По уравнению движения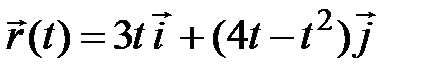 
определите траекторию движения (годограф), вектор скорости, вектор ускорения, тангенциальную и нормальную составляющие вектора ускорения для моментов 
и 
.
б) По уравнению движения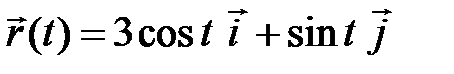 
определите траекторию движения (годограф), вектор скорости, вектор ускорения, тангенциальную и нормальную составляющие вектора ускорения для моментов и .
в). Найдите кривизну в вершинах эллипса 
в вершинах эллипса.
15.Полярная система координат:
а) Постройте кривые в полярной системе координат:
, 
, 
, 
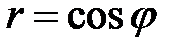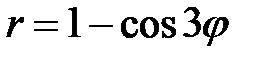б) Найти площадь фигуры, ограниченной какой-либо кривой, указанной в предыдущем задании
в) Найдите длину дуги кривой 
Контрольные вопросы
1. Линейные операции над векторами
2. Векторный базис в пространстве n-измерений. Условия существования базиса.
3. Прямоугольный декартов базис. Координаты вектора в этом базисе. Модуль вектора.
4. Направляющие косинусы. Единичный вектор (орт).
5. Скалярное произведение векторов. Определение. Свойства. Вычисление.
6. Векторное произведение векторов. Определение. Свойства. Вычисление.
7. Смешанное произведение векторов. Определение. Свойства. Вычисление.
8. Уравнения прямой на плоскости: с направляющим вектором, через две точки, в «отрезках на осях», с угловым коэффициентом. Общее уравнение прямой.
9. Канонические уравнения и характеристики кривых второго порядка
10. Эксцентриситет эллипса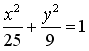 
равен…
11. Если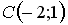 
- центр окружности, которая проходит через точку 
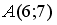, то уравнение этой окружности имеет вид …
Самостоятельная работа
РГР № 9 (0,278 ЗЕ)
Поверхности второго порядка, плоскости и прямые в пространстве
Срок выполнения 13-17 недели
Содержание работы
1. Задачи по линейным объектам в пространстве (плоскости, прямые)
2. Выписать канонические уравнения основных поверхностей второго порядка и схематично их построить
3. По приведенным уравнениям поверхностей описать их свойства и схематично построить поверхности
Литература [1,7,17]
1. Векторы 
образуют ортонормированный базис. Найти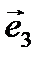 
, если известны 
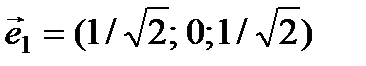и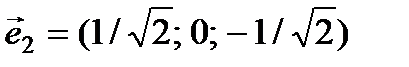 
.
2. В точке 
приложена равнодействующая сил 
. Найдите вектор момента равнодействующей этих сил относительно точки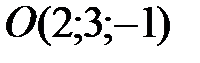 
. Ответ: 
3. При каких значениях параметра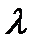 
векторы 
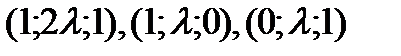компланарны?
4. Координаты вершин тетраэдра 
, 
, 
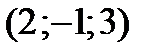
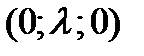, а его объем равен 5. Найти значение неизвестной координаты.
5. Найдите угол между прямыми:
6. Найдите угол между прямой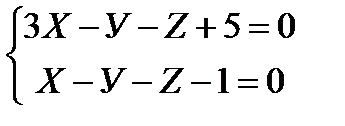 
и
плоскостью 4Х–8У+Z–3=0;
7. Найдите точку пересечения прямой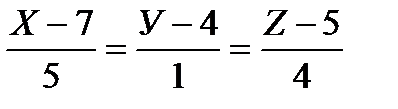 
и
плоскости 3Х–У+2Z–5=0
8. Запишите уравнение плоскости, проходящей через точку М (3; 4; 1) перпендикулярно прямой Х=5–t; У=4t; Z= -2+t;
9. Покажите, что прямые 
и Х=7+3t; У=2+2t; Z=1–2t
лежат в одной плоскости и найдите её уравнение
10. Напишите уравнение плоскости, проходящей через прямые и найдите
расстояние между ними:
; 
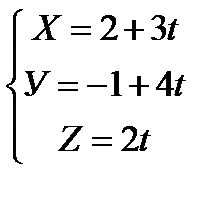11.Постройте поверхности методом сечений и назовите их
(Х–2)2+(У–2)2+(Z+5)2=16;
Х2+У2+Z2–4Х–2У+2Z–19=0;
Х2+У2+Z2+20У=0;
;
;
Х2+У2–Z2= –1;
Х=Z2+У2;
Х2–У2=Z2;
Z=2+Х2+У2;
Х2–У2+Z2+4=0;
Х2+У2–Z2=4;
Х2+У2=4Х;
Z=4–У2;
Х2–У2=Z;
Z=ХУ;
12) 
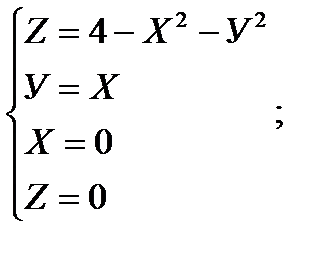13) 
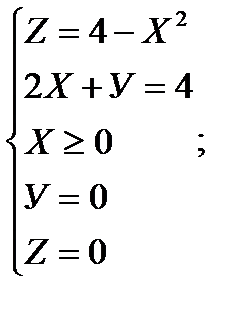14) 
Контрольные вопросы
1. Дайте вывод общего уравнения плоскости в пространстве. Дайте определение вектора нормали
2. Нормальное уравнение плоскости. Расстояние от точки до плоскости. Найдите расстояние от начала координат до плоскости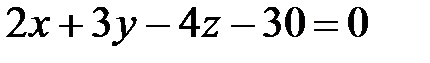 
3. Найдите точку пересечения плоскости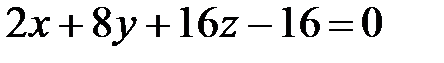 
с осью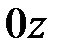 
4. Дайте вывод уравнения прямой: канонические, параметрические, через две точки
5. Общее уравнение прямой линии в пространстве. Переход от общего уравнения прямой к каноническому.
6. Условие параллельности плоскостей. Условие параллельности прямых.
7. Условие перпендикулярности плоскостей, условие перпендикулярности прямых.
8. Условие пересечения прямых в пространстве
9. Какая кривая является сечением поверхности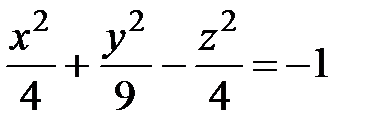 
плоскостью а) 
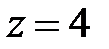, б)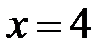 
?
10. Прямая 
пересекает плоскость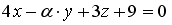 
только в том случае, когда 
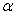не равно …
Самостоятельная работа
РГР № 10 (0,278 ЗЕ)
Локальные экстремумы функций
нескольких переменных
Срок выполнения 16-17 недели
Содержание работы
1. Запись дифференциалов первого и второго порядков для функции двух и трех переменных
2. Задачи на локальный экстремум
3. Задачи на условный экстремум
4. Наибольшее и наименьшее значения функции в замкнутой ограниченной области
Литература [1,2,17]
Элементы теории
Вычисление частных производных производится по тем же правилам, что и вычисление функций одной переменной, считая все переменные постоянными, кроме той, по которой ведется дифференцирование.
Первым дифференциалом 
называют линейную относительно приращений 
часть полного приращения функции, которая для функции двух переменных имеет вид:
,
а для функции трех переменных:
.
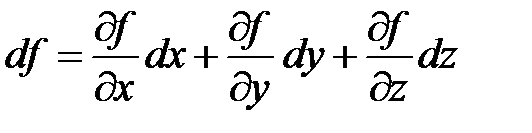Производная по направлению задает скорость изменения функции в заданной точке по заданному направлению 
:
.
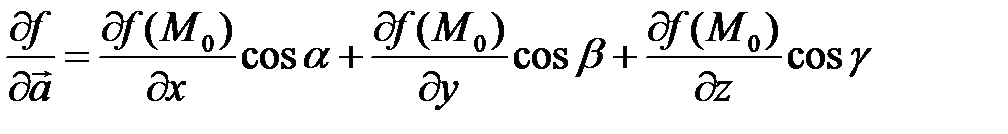Градиентом дифференцируемой функции называют вектор, координатами которого являются частные производные в заданной точке:
.
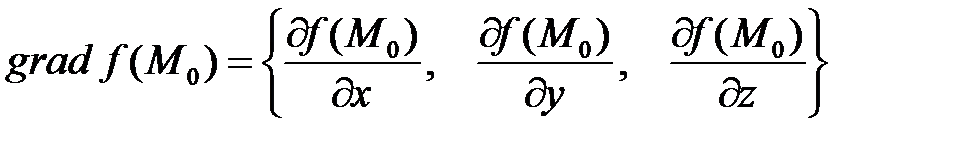Производная по направлению является проекцией вектора градиента на это направление:
.
Анализ последнего выражения показывает, что градиент является направлением, скорость изменения функции вдоль которого максимальна.
Касательная плоскость содержит касательные ко всем кривым, проходящим через данную точку поверхности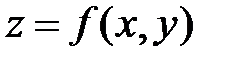 
:
.
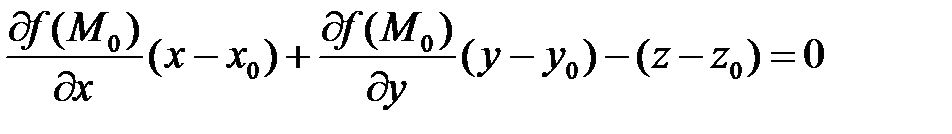Производную сложной функции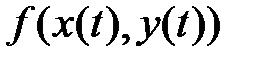 
находим по правилу
,
а производные сложной функции 
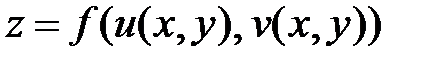согласно правилу:
.
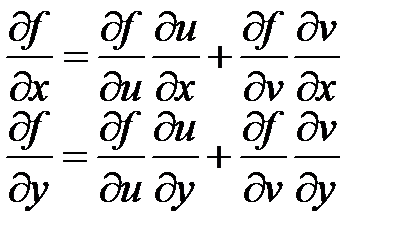Производную функции, заданной неявно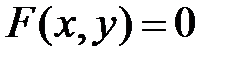 
, находят согласно правилу:
.
Для функции 
определены производные второго порядка:
, 
, 
, 
.
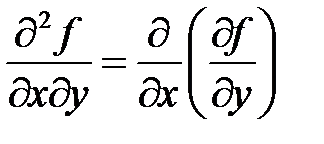Для функции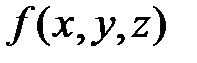 
, кроме указанных выше производных, определены следующие производные второго порядка:
, 
, 
, 
, 
.
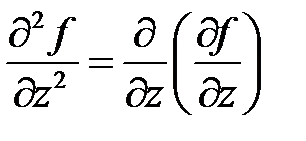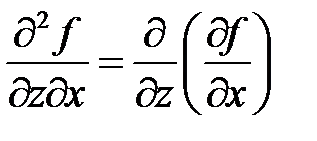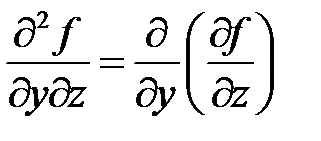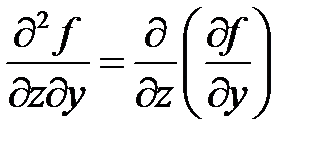Заметим, что в точках непрерывности смешанные частные производные равны.
Дифференциалы второго порядка определяются согласно соотношениям:
,
.
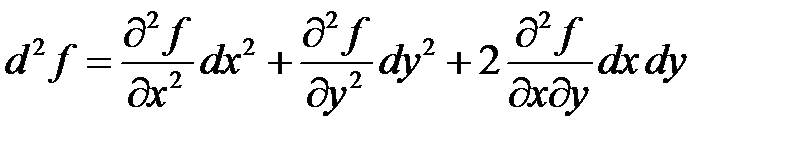Формула Тейлора в окрестности точки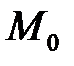 
с точностью до бесконечно малых второго порядка имеет вид:
Точкой локального экстремума называют точку непрерывности функции 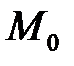, в окрестности которой приращение функции сохраняет знак: 
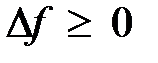- точка локального минимума, 
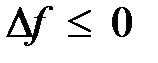- точка локального максимума. Необходимые условия существования экстремума записываются следующим образом:
,
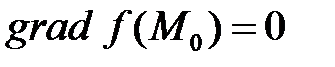что равносильно системе уравнений для нахождения критических точек функции:
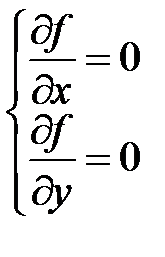или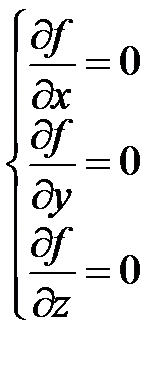 
.
Достаточные условия существования экстремума определяются знаком приращения функции, который в свою очередь определяется знаком второго дифференциала:
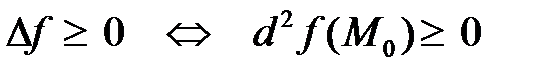, то точка 
является точкой локального минимума,
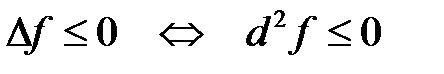, то точка является точкой локального максимума.
По своей структуре второй дифференциал является является квадратичной формой относительно дифференциалов 
и ему ставится в соответствие матрица:
.
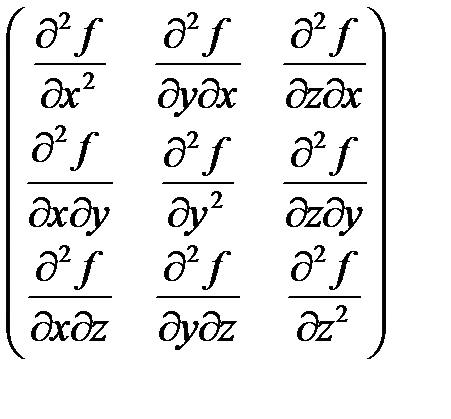Согласно критерию Сильвестра квадратичная форма является положительно определенной, если положительны все главные диагональные миноры этой матрицы:
, 
, 
.
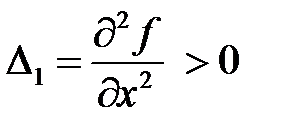(условия существования локального минимума), и является отрицательно определенной при условии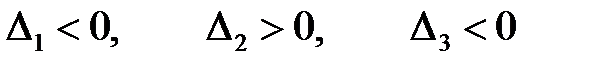 
(условия существования локального максимума).
Для нахождения точек условного экстремума исследуют на обычный экстремум функцию Лагранжа
.
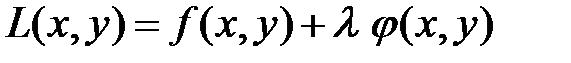Здесь 
- условие связи, а 
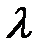- множитель Лагранжа. При этом достаточные условия существования экстремума выражаются через знак второго дифференциала 
(условие минимума),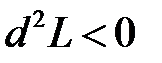 
- условие максимума. Знак второго дифференциала можно анализировать непосредственно при наличии условий связи.
Задачи
1. Запишите производные второго порядка для указанной функции, в указанной точке.
Запишите второй дифференциал.
Запишите матрицу, соответствующую d2f.
Запишите разложение по формуле Тейлора в указанной точке:
а)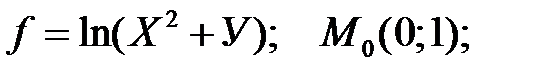 
б)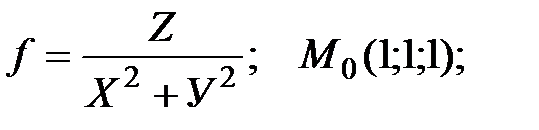 
2. Исследуйте функцию на локальный экстремум:
а) 
| б)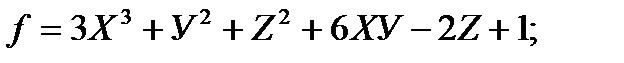 
|
в)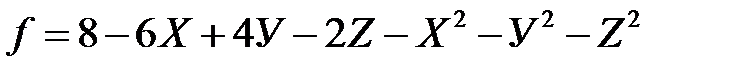 
|
3. На эллипсоиде Х2+2У2+4Z2=8 найти точку, наиболее удалённую от М0(0;0;3).
