Министерство образования и науки Российской федерации
Государственное бюджетное образовательное учреждение
высшего профессионального образования
«Кузбасский государственный технический университет» им. Т.Ф. Горбачева
Г.А. Казунина, Г.А. Липина
Методические указания к выполнению самостоятельной работы
по курсу математики (1 семестр) для студентов направления подготовки 140400.62 «Электроэнергетика и электротехника»
Рекомендовано в качестве учебного пособия
учебно-методической комиссией направления
140400.62 «Электроэнергетика и электротехника»
Кемерово 2012
Рецензенты:
Жирнова Т.С. – доцент кафедры математики
Завьялов В.М. – председатель УМК направления подготовки 140400.62
«Электроэнергетика и электротехника»
Казунина Галина Алексеевна, Липина Галина Александровна. Методические указания к выполнению самостоятельной работы по курсу математики (1семестр) для студентов направления подготовки 140400.62 «Электроэнергетика и электротехника»: учеб.пособие [Электронный ресурс]: для организации самостоятельной работы студентов - бакалавров направления подготовки 140400.62 «Электроэнергетика и электротехника»/ Г.А. Казунина, Г.А. Липина - Электрон.дан.- Кемерово: КузГТУ, 2012.- 1электрон.опт.диск(CD-ROM); 12 см.- Систем. требования: любой компьютер, поддерживающий Microsoft Windows –97 и выше, мышь.- Загл. с экрана.
Приводится содержание самостоятельной работы студентов по темам курса математики, которые согласно рабочей программе изучаются в 1 семестре. Для лучшего усвоения материала изложение сопровождается контрольными вопросами. Пособие предназначено для организации самостоятельной работы студентов
ÓГУ КузГТУ
ÓКазунина Г.А.
Липина Г.А.
РГР № 1 (0,138 ЗЕ)
Пределы: а) Раскрытие неопределенностей
Б) Непрерывность. Точки разрыва
Срок выполнения 1-2 недели семестра
Содержание работы
1. Раскрытие неопределенности 
2. Порядок малости бесконечно малых. Эквивалентные бесконечно малые.
3. Раскрытие неопределенности 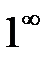
4. Определение характера точек разрыва функции
5. Контрольные вопросы
Литература [1,2,8,14,17]
1. Раскрыть неопределенности
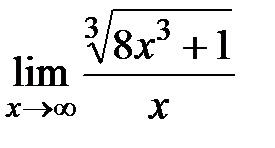 ,
, 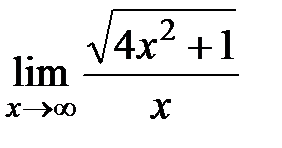 ,
, 
 ,
,  ,
, 
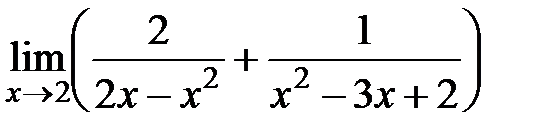 ,
,  .
.
2. Раскрыть неопределенности, используя эквивалентные бесконечно малые функции
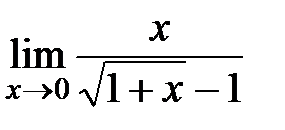 ,
,  ,
,  ,
,
 ,
, 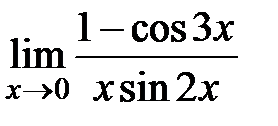
3. Раскрыть неопределенности
 ,
,  ,
,  ,
, 
 ,
,  ,
, 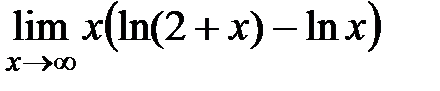
4. По формулам функций схематически построить их графики. В точках разрыва вычислить односторонние пределы и указать характер точек разрыва:




 ,
,  ,
,  .
.
Контрольные вопросы
1. Свойства функций: четность, периодичность, монотонность, нули функции.
2. Свойства и графики основных элементарных функций: степенная, показательная, логарифмическая, тригонометрические функции, обратные тригонометрические функции, гиперболические функции, обратные гиперболические функции
3. Дайте определение обратной функции. Для указанных функций найти выражение для обратной функции. Построить в одних координатных осях графики прямой и обратной функций:  ,
,  ,
,  ,
,  ,
,  ,
, 
4. Установите соответствие между периодической функцией и значением ее периода 1.  2. 2.  3. 3. 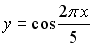
| |||||||||||||||
ВАРИАНТЫ ОТВЕТОВ:
|
5. Первый замечательный предел
6. Второй замечательный предел
Приведите примеры основных элементарных функций, которые являются четными
8. Приведите примеры основных элементарных функций, которые являются нечетными
9. Приведите примеры основных элементарных функций, которые являются бесконечно малыми в окрестности нуля.
10. Приведите примеры основных элементарных функций, которые являются ограниченными на бесконечности
11. Приведите примеры основных элементарных функций, которые являются бесконечно большими в окрестности нуля
12. Опишите основные свойства функции по формуле:  ,
,  ,
,
 ,
,  ,
, 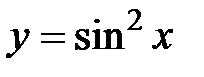 ,
, 
13. Что такое неопределенности? Перечислите основные неопределенности.
14. Какие способы раскрытия неопределенности  при условии
при условии  Вы знаете? Приведите примеры.
Вы знаете? Приведите примеры.
15. Приведите пример раскрытия неопределенности  при условии
при условии 
16. Дайте определение функции, непрерывной в точке
17. Дайте определение точки разрыва первого рода. Приведите примеры
18. Приведите примеры точки устранимого разрыва
19. Дайте определение точки разрыва второго рода. Приведите примеры.
20. Установите соответствие между пределом и его значением 1. 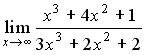 2. 2. 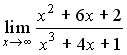 3. 3. 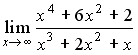 4. 4. 
| |||||||||||||||
ВАРИАНТЫ ОТВЕТОВ:
|
РГР № 2 (0,138 ЗЕ)
Техника дифференцирования
Срок выполнения 1-2 недели семестра
Содержание работы
1. Таблица производных. Производные арифметических операций
2. Производная сложной функции
3. Производная функции, заданной неявно
4. Производная функции, заданной параметрически
5. Дифференциал. Применение к приближенным вычислениям
6. Геометрический смысл производной. Уравнение касательной
7. Механический смысл производной
8. Контрольные вопросы
Литература [1,2,8,17]
1. Вычислить производные, используя линейность операции дифференцирования и правила дифференцирования произведения и частного:


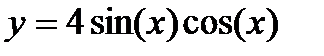









2. Вычислить производные, используя правило дифференцирования сложной функции (выписывать цепочку промежуточных переменных):

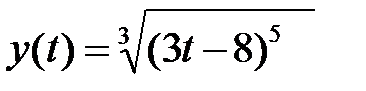




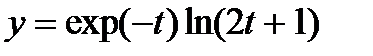
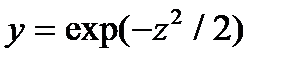


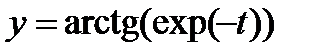


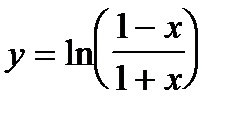



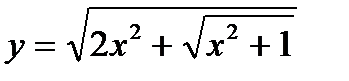


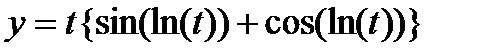
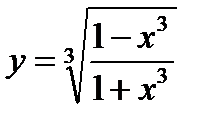



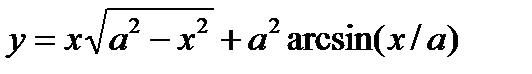
3. Найти производную функции, заданной неявно:
 а)
а)  ; б)
; б) 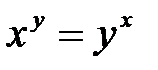
4. Найти производную функции, заданной параметрически:
а) 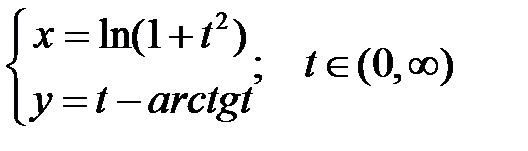 ; б)
; б) 
5. Применение дифференциала для приближенных вычислений
а) Найдите приближенное выражение для приращения объема 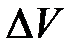 при изменении давления на
при изменении давления на  при условии постоянства температуры
при условии постоянства температуры  , если
, если  связаны законом
связаны законом 
б) Вычислить приближенно значение функции при помощи дифференциала 
6. Геометрический смысл производной
а) Под каким углом график функции 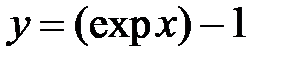 пересекает ось абсцисс?
пересекает ось абсцисс?
б) В каких точках и под каким углом пересекаются графики функций
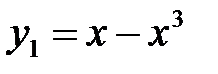 и
и 
в) Напишите уравнение касательной к кривой в указанной точке

6. Физический смысл производной:
а) Точка движется по параболе 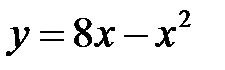 так, что ее абсцисса изменяется по закону
так, что ее абсцисса изменяется по закону 
 (
( -измеряется в метрах, а
-измеряется в метрах, а  - в секундах). Какова скорость изменения ординаты через 9 сек после начала движения?
- в секундах). Какова скорость изменения ординаты через 9 сек после начала движения?
б) В какой момент  надо устранить действие сил, чтобы
надо устранить действие сил, чтобы
точка,участвующая в гармоническом колебании 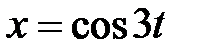 , продолжала двигаться равномерно со скоростью
, продолжала двигаться равномерно со скоростью 
Контрольные вопросы
1. Дайте определение дифференцируемой функции и производной в точке
2. В чем состоит геометрический смысл производной?
3. В чем состоит физический смысл производной?
4. Как связаны производные прямой и обратной функции?
5. Сформулируйте правило дифференцирования сложной функции
6. На рисунке изображен график функции  , заданной на интервале
, заданной на интервале  .
.
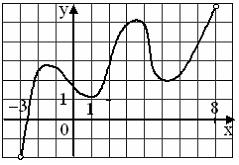
Тогда число интервалов, на которых касательная к графику функции  имеет положительный угловой коэффициент, равно …
имеет положительный угловой коэффициент, равно …
7.
РГР № 3 (0,417 ЗЕ)