Гипотеза – утверждение
Опред: Стат. гипотеза – утверждение о значении пар-ра θ.
Стат. гипотеза м.б. записана в виде 
Опред: стат. гипотеза простая, если 
- одноточечное.
В прот. случае стат. гип. – сложная
Задача: Выдвигается основная гип. 
и альтернативная (несколько)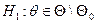 
По результатам наблюдений надо выбрать Н0 или Н1
Правило выбора – критерий.
Опред: Критерий 
Значение 
вероятность отвергнуть осн. гипотезу по результатам наблюдений 
Согласно критерию область 
разбивается на 3 части:
Доверит. 
| Обл. сомнений 
| Критическая область 
|
Опред: Критерий j - нерандомизированный, если j(Х)={0,1}(или Рθ(j(Х) Î (0,1))=0 "θ)
В противном случае 
j - рандомизированный.
4. Выборочный метод. Эмпирическая функция распределения. Теорема Гливенко – Кантелли (план док-ва). Преобразование Смирнова. Теорема Колмогорова. Оценивание теоретической функции распределения эмпирической. Гистограмма и полигон частот.
Пусть (Х1 … Хn) выборка из распределения Рθ . Истинное значение Рθ - теоретическое распределение.
Эмпирическая функция распределения – функция следующего вида:
Fn(x) = 1/n* 
, где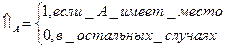 
Т.е. ее значение в точке х равно отношению числа наблюдений меньше х к общему числу наблюдений.
Теорема (Гливенко – Кантелли)
Пусть(Х1 … Хn) выборка из распределения с ф.р. F,тогда sup|Fn(x)-F(x)| почти наверное->0
План док-ва:
доказывается сходимость на ограниченном интервале (т.к. F неубывает и ограничена). Показывается, что изменение между двумя соседними точками мало. Доказывается, что сходимость на концах следует из: 
-> sup|Fn(x)-F(x)|->0
Преобразование Смирнова
Пусть Х случайная величина с ф.р. F (непрерывна),тогда F(x)=Y-новая с.в. имеющая равномерное распределение U(0,1), т.е.:
Если F строго возрастает, то 
: 
Теорема Колмогорова
Пусть (Х1 … Хn) выборка из распределения F(непрер.),тогда 
, где К – распр-е Колмогорова, т.е.:
, где 
С ростом n, эмпирическая ф.р. приближается к теоретической. У э.ф.р. имеется 
-окрестность, по т. Гливенко – Кантелли вероятность того, что истинная ф.р. лежит в этой эмпирической -окрестности ->1 при 
.
По т. Колмогорова, вероятность того, что истинная ф.р. лежит в 
- окрестности эмпирической стремится к пределу K(), где К(х) – ф.р. Колмогорова.
Пусть 
>0 – маленькое число, F – истинная ф.р., тогда если F0=F, где F0 предполагаемая ф.р., то с вероятностью 
, т.е.
- доверительный интервал для теоретической ф.р.
Гистограмма и полигон частот:
Один из способов наглядного представления статистических данных – Гистограмма частот. Область значений с.в. разбивается на равные интервалы, подсчитывается число значений с.в. попавших в интервал и на каждом интервале строится прямоугольник, с основанием на этот интервал и высотой V/(nh), где V – число выборочных точек попавших в этот интервал, n – объем выборки, h – длина интервала. Площадь каждого такого прямоугольника по т Бернулли будет сходится при n-> 
к вероятности попадания с.в. в интервал.
Для оценки гладких плотностей используют методику, основанную на полигоне частот – ломаной кривой, строящейся следующим образом: если построена гистограмма частот, то ординаты ее средних точек на каждом из интервалов последовательно соединяются отрезками прямых. Гистограмма и полигон – статистические аналоги теоретической плотности.
