Основные понятия математической статистики. Статистический эксперимент. Способы накопления статистической информации. Понятие выборки.
Математическая статистика занимается составлением выводов об имеющихся данных (о модели эксперимента).
Базовое вероятностное пространство (Ω,₣,Ρ)
Частный случай – распределение случайного вектора:
Ω=Х=Rn; ₣=Дn – борелевская σ-алгебра; Ρ – распределение вероятностей
Получили более мелкое пространство, которое удобно использовать при работе с моделями математической статистики (Х, Дn,Ρ).
Статистический эксперимент – тройка объектов (Х, Дn, Ρ), где Ρ ={Рθ,θєΘ} - семейство вероятностей.
Стандартные предположения о семействе Ρ:
(1) Рθ =Рθ1 * Рθ2 …*Рθn, т.е. результат наблюдений (Х1 … Хn) є Rn – независимые случайные величины при V θєΘ
(2) Рθ1=Рθ2=…=Рθn, т.е. результат наблюдений (Х1 … Хn) є Rn – независимые одинаково распределенные случайные величины (НОРСВ).
Если (1) и (2) выполнены, то (Х1 … Хn) – выборка – набор независимых одинаково распределенных наблюдений.
В задачу математической статистики входит только анализ данных и их интерпретация.
Выбор модели определяется характером полученных данных и не входит в задачу математической статистики. Семейство вероятностей Ρ определяется целью статистических исследований (априорной информацией), поэтому Ρ может быть параметризованно по-разному.
Пусть имеется совокупность результатов эксперимента (генеральная совокупность), тогда выборка – набор элементов однородной генеральной совокупности.
Задача математической статистики – сделать выводы о характере распределения генеральной совокупности по выборке. Роль генеральной совокупности в нашей модели играет теоретическое распределение.
Рθ - теоретическое значение распределения, соответствует распределению генеральной совокупности.
Типы задач математической статистики:
Точное оценивание – по результатам наблюдений выбрать значение Рθє Ρ, которое оптимальным образом согласуется с данными.
Интервальное оценивание - по результатам наблюдений выбрать область
Θ0 (Х1 … Хn) С Θ т.ч. при V θєΘ Рθ(Θ0 (Х1 … Хn) э θ)≥1-α, где α - определенное маленькое число. Т.е. выбор такого множества, которое накрывает теоретическое значение параметра с вероятностью не меньше (1-α).
Проверка статистических гипотез – по результатам наблюдений выбрать из
Н1… Нn наиболее подходящую, где Нi – взаимоисключающие гипотезы (предположения о значении параметров Нi: θєΘi; Θi∩Θi=0; UΘi=Θ).
Примеры параметрических семейств распределений.
1) Распределение Бернулли: Bi(1, p)- биномиальное распределение с параметрами 1 и p.
Дискретное распределение, сконцентрированное в точках {0;1}; P(X1=1)=p. Параметр θ=p  [0;1]
[0;1]
2)Биномиальное распределение
Дискретное распределение, сконцентрированное в точках {0,1…}
P(X1=k)=Cmk pk (1-p)m-k, k=0,1…m
Параметр θ=(m,p). m  N, p
N, p  [0,1]
[0,1]
3)Семейство распределений Пуассона Pas(λ).
Дискр. распр., неотрицательное, сконцентрированное в точках {0,1…}
P(X=k)= λk\(k!)*exp(-λ), k=0,1… θ = λ
4)Геометрическое распр Geom(p)
Дискретное, значения N 
P(X1=k)=p (1-p)k, k=0,1,… θ =p
5)Нормальное, абсолютно непрерывное распределение N(a, σ2).
p θ (x)= 
Параметр 
6) Показательное Exp(α)
Абсолютно непрерывное

Параметр θ = α>0
7)распределение Лапласа L(a,b)
Абсолютно непрерывное
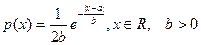
8)Гамма Г(α,p)
Абсолютно непрерывное







