1. Решение задач на множества, простые и сложные проценты.
2. Вычисление числа перестановок, сочетаний, размещений (комбинаторика).
3. Решение задач на вероятность наступления зависимых и независимых, совместных и несовместных событий с применением основных теорем теории вероятностей.
4. Вычисление статистических характеристик и построение гистограммы на примере данных по срокам лишения свободы осужденных.
5. Выбор и построение наиболее информативных графиков для представления результатов статистической обработки данных учетов правовых органов.
Примеры тестовых заданий для самоконтроля
Задание № 1. Заданы множества A={1,2,3} и B={1,2,3,4,5}, тогда для них верным утверждением будет…
Варианты ответов
а) «Множество А есть подмножество множества В»
б) «Множество А включает в себя множество В»
в) «Множества А и В равны»
Задание № 2. Отношение задано неравенством: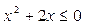 
, тогда данному отношению принадлежит следующий интервал…
Варианты ответов
а) (0;2) б) (-2;0) в) (1;3) г) (-1;1)
 |
Задание № 3. Пусть А и В - множества, изображенные на рисунке:
Тогда объединением этих множеств является …
Варианты ответов
а) А\В б) 0 в) А г) В
Задание № 4. В слове «Word» меняют местами буквы. Тогда количество всех возможных различных «слов» равно …
Варианты ответов
а) 20 б)16 в) 8 г) 24
Задание № 5. Количество различных двухзначных чисел, которые можно составить из четырех цифр: 1, 2, 3, 4 (все цифры в числе разные), равно …
Варианты ответов
а) 6 б) 4 в) 24 г) 12
Задание № 6. Количество различных способов выбора (порядок не имеет значения) 2 томов из 12 – томного собрания сочинения Л.Н. Толстого равно ….
Варианты ответов
а) 24 б) 132 в) 2 г) 66
Задание № 7. На факультете учатся студенты, получающие стипендию и студенты, не получающие стипендию. Пусть А – множество всех студентов факультета, В – множество всех студентов факультета, получающих стипендию. Тогда пересечением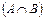 
этих множеств будет …
Варианты ответов
а) множество студентов факультета, получающих стипендию
б) множество студентов факультета, не получающих стипендию
в) пустое множество
г) множество всех студентов факультета
Задание № 8. Игральный кубик бросают один раз. Тогда вероятность того, что на верхней грани выпадет число очков больше, чем три, равна…
Варианты ответов
а) 1/3 б) 1 в) 1/2 г) 0
Задание № 9. Для посева берут семена из двух пакетов. Вероятности прорастания семян в первом и втором пакетах соответственно равны 0.9 и 0.7. Взяли по одному семени из каждого пакета, тогда вероятность того, что оба они прорастут равна …
Варианты ответов
а) 0.8 б) 0.63 в) 0.9 г) 1.6
Задание № 10. Вероятность наступления некоторого события не может быть равна…
Варианты ответов
а) 1 б) 2 в) 0 г) 1/2
Задание № 11. Дискретная случайная величина Х имеет закон распределения вероятности:
| Х | ||
| Р | 0.4 | 0.6 |
Тогда математическое ожидание 
этой случайной величины равно…
Варианты ответов
а) 1 б) 2.2 в) 5 г) 2.8
Задание № 12. В урне находится 6 шаров: 3 белых и 3 черных. Событие А – вынули белый шар, событие В – вынули черный шар. Опыт состоит в выборе только одного шара. Тогда для этих событий неверным будет утверждение:
Варианты ответов
а) Вероятность события В равна ½
б) События А и В равновероятны
в) События А и В несовместны
г) Событие А невозможно
Задание № 13. По статистическому распределению выборки
установить ее объем
| |||
|
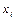
Варианты ответов
а) 11 б) 30 в) 25 г) 13
Задание № 14. Средняя выборочная вариационного ряда 1, 2, 3, 3, 4, 5 равна…
Варианты ответов
а) 3 б) 6 в) 2.5 г) 3.6
Задание № 15. Для дискретной случайной величины Х задан закон распределения вероятности:
| Х | ||
| Р | 0.4 |
Тогда значение пустой клетки равно…
Варианты ответов
а) 0.1 б) 0.16 в) 0.6 г) 0.8
Задание № 16. В результате 10 опытов получена следующая выборка:
2, 2, 2, 3, 4, 4, 6, 6, 6, 6
тогда для нее законом распределения будет…
Варианты ответов
а)
|
| ||||
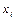
| 0.3 | 0.1 | 0.2 | 0.4 |
б)
|
| ||||
|
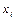
| 0.6 | 0.2 | 0.4 | 0.6 |
в)
| ||||
|
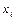
| 0.3 | 0.1 | 0.2 | 0.3 |
г)
|
| ||||
|
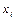
| 0.3 | 0.1 | 0.2 | 0.4 |
Задание № 17. Значение 5! равно…
Варианты ответов
а) 5 б) 25 в) 120 г) 125
Задание № 18. Двое играют в шахматы. Событие А означает, что выиграл первый игрок, событие В – что выиграл второй игрок. Событие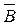 
означает
Варианты ответов
а) Первый игрок выиграл или сыграл вничью
б) Второй игрок выиграл или сыграл вничью
в) Партия закончилась в ничью
г) Возможен любой исход партии
Задание № 19. Закон распределения случайной величины Х имеет вид:
| ||||
| 0.3 | 0.1 | 0.2 | 0.4 |
Математическое ожидание её равно …
Варианты ответов
а) 0.11 б) 1.1 в) 1.5 г) 6
Задание № 20. Закон распределения случайной величины Х имеет вид:
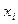
| -1 | |||
|
| 0.4 | 0.3 | 0.1 |
В свободной клетке стоит число …
Варианты ответов
а) 0.2 б) 0.1 в) 0.5 г) -0.2
Задание № 21. Задана выборка 0, 1, 2, 2, 0, 1, 1, -1, 0. Ее вариационный ряд имеет вид…
Варианты ответов
а)
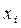
| -1 | |||
|
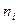
б) 2, 2, 1, 1, 1, 0, 0, 0, -1
в) -1, 0, 0, 0, 1, 1, 1, 2, 2
г)
| -1 | |||
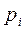
| 0.3 | 0.2 | 0.1 | 0.4 |
Задание № 22. Число сочетаний С32 равно …
Варианты ответов
а) 6 б) 5 в) 3 г) 1
Задание № 23. Даны два множества А=(-1;1] и B=[0;2]. Их пересечение не содержит число...
Варианты ответов
а) 0 б) 1 в) 2 г) 0.5
Задание №24. В результате 10 опытов получена выборка 1,0,1,2,2,1,0,0,2,3. Выборочное среднее равно …
Варианты ответов
а) 1.2 б) 12 в) 3 г) 2
Задание № 25. В забеге участвуют 3 спортсмена. Вероятность ими выполнить норму равна 
, 
и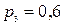 
соответственно. Вероятность того, что все они выполнят норму, равна…
Варианты ответов
а) 1.8 б) 0.192 в) 1.92 г) 19.2
Задание № 26. Цифры 1, 5, 7, 9 написаны на четырех карточках. Сколько различных четырехзначных числа можно составить из этих карточек?
Варианты ответов
а) 24 б) 10 в) 14 г) 18
Задание № 27. Дисперсия случайной величины не может быть равна…
Варианты ответов
а) -2 б) 1 в) 0 г) 365
Задание № 28. Выигрыш по билету беспроигрышной лотереи есть событие…
Варианты ответов
а) Невозможное б) Достоверное
в) Противоположное г) Нереальное
Задание № 29. На экзамен пришло 30 студентов. 20 из них сдало экзамен. Частота наступления события «экзамен сдан» равна…
Варианты ответов
а) 2/3 б) 3/2 в) 1 г) 1.5
Задание № 30. Выбирают наугад число от 1 до 100. Вероятность того, что это не окажется число 10, равна…
Варианты ответов
а) 1/100 б) 1/10 в) 10 г) 0.99
Задание № 31. Заданы два множества А ={1;3} и B={3;7}. Объединением А и В является….
Варианты ответов
а) {1,3,3,7} б) {3} в) {1,3,7} г) {1,7}
Задание № 32. Для множества {1,2,3} сочетаниями по два элемента являются…
Варианты ответов
а) {1,2}, {1,3}, {2,3}, {2,1}, {3,1}, {3,2}
б) {1,2}, {1,3}, {2,3}
в) {1,2}, {1,3}, {2,3}, {2,1}, {3,1}, {3,2}, {1,1}, {2,2}, {3,3}
г) {1,2}, {1,3}, {2,3}, {1,1}, {2,2}, {3,3}
Задание № 33. Научно-обоснованный перечень признаков (или вопросов), подлежащих регистрации в процессе наблюдения называется:
a) опросным листом,
b) журналом регистрации,
c) программой наблюдений,
d) статистическим формуляром.
Задание № 34. Упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку называется:
a) анализом,
b) рядом распределения,
c) наблюдением,
d) формуляром.
Задание № 35. Обработка и подсчет первичных данных, непосредственно собранных в процессе статистического наблюдения называется:
a) группировкой,
b) вторичной сводкой,
c) централизованной сводкой,
d) первичной сводкой.
Задание № 36. Отрасль статистической науки, изучающая количественную сторону массовых правовых и других юридически значимых явлений и процессов называется …? статистикой:
a) социальной,
b) судебной,
c) моральной,
d) административной.
Задание № 37. Наглядное изображение статистических величин при помощи геометрических линий и фигур называется:
a) статистический график,
b) статистический чертеж,
c) статистическая схема,
d) статистическая таблица.
Задание № 38. Отдельные значения признаков в вариационном ряду называются:
a) дискреты,
b) варианты,
c) отсчеты,
d) частоты.
Задание № 39. Численности отдельных вариантов, показывающие как часто встречаются те или иные варианты в ряду распределения называются:
a) отсчеты,
b) варианты,
c) дискреты,
d) частоты.
Задание № 40. Выражение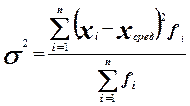 
используется для вычисления:
a) вариации количественного признака,
b) дисперсии качественного признака,
c) вариации качественного признака,
d) дисперсии количественного признака.
ЛИТЕРАТУРА
Основная литература
1. Информатика и математика для юристов: учебник для студентов вузов, обучающихся по юридическим специальностям / Под ред. С.. Казанцева, Н.М. Дубининой. – М.: Юнити-Дана, 2009. – 560 с.*
2. Крахин А.В. Математика для юристов: Учебное пособие. – М.: Флинта, 2005. – 200 с. *
3. Попов, А.М., Сотников В.Н., Е.И. Нагаева. Информатика и математика для юристов: учебник для студентов вузов, обучающихся по специальности «Юриспруденция» / А.М. Попов и [и др]; под ред. проф. А.М. Попова.– М.: Юнити-Дана, 2009. – 391 с. *
4. Правовая статистика: учебник / Под ред. проф. С.Я. Казанцева, проф. С.Я. Лебедева. – М.: Юнити-Дана, 2008. – 255 с.*
Дополнительная литература
1. Богатов Д. Ф., Богатов Ф. Г. Конспект лекций и практикум по математике для юристов: Учебное пособие для юристов / Д. Ф. Богатов, Ф. Г. Богатов. – М: Приор-издат, 2003. – 448 с.*
2. Богатов Д. Ф., Богатов Ф. Г. Математика для юристов в вопросах и ответах: Учебное пособие для образовательных учреждений юридического профиля / Д. Ф. Богатов, Ф. Г. Богатов. – М: Приор-издат, 2001. – 272 с.
3. Воронов М. В., Мещерякова Г. П. Математика для студентов гуманитарных факультетов / М. В. Воронов, Г. П. Мещерякова. – Ростов н/Д: «Феникс», 2002. – 384 с.*
4. Информатика и математика: учебно-методические материалы для студентов заочной формы обучения. – М: Российская академия правосудия, 2002. – 40 с.*
5. Квачко, В. Ю., В. Т. Королев, Родионов В. В. Математика для юристов: Курс лекций / В. Ю. Квачко, В. Т. Королев, В. В. Родионов. – М.: Российская академия правосудия, 2004. – 179 с.*
Интернет-ресурсы
1. Материал из Википедии — свободной энциклопедии [Электронный ресурс]. – Режим доступа: http://ru.wikipedia.org/wiki/, свободный.
2. Математика для юристов: обучающий видеокурс [Электронный ресурс], 2009. – Режим доступа: http://www.TeachVideo.ru, свободный.*
Вопросы для подготовки к зачету
1. Предмет математики. Математический язык: особенность, становление, развитие. Греческий алфавит.
2. Основные понятия теории множеств. Основные операции над множествами. Аксиомы алгебры множеств.
3. Элементы математической логики. Операции над высказываниями. Основные логические операции.
4. Элементы комбинаторики. Комбинаторные задачи и методы их решения.
5. Перестановки, размещения, сочетания.
6. Натуральные, целые и рациональные числа. Десятичные дроби и вещественные числа. Округление дробей. Стандартная форма записи чисел. Проценты.
7. Позиционные системы счисления. Правила перевода чисел из одной системы исчисления в другую.
8. Понятие функции. Свойства функций. Сложная функция.
9. Способы задания функции.
10. Элементы теории вероятностей. Классическое определение вероятности. Свойства вероятности.
11. Случайные события: совместные, несовместные; зависимые, независимые; противоположные. Операции над случайными событиями.
12. Теоремы сложения и умножения вероятностей. Формула полной вероятности.
13. Понятие случайной величины. Дискретные и непрерывные случайные величины. Законы распределения вероятностей дискретной случайной величины.
14. Числовые характеристики дискретных случайных величин.
15. Функции распределения вероятностей случайных величин.
16. Числовые характеристики непрерывных случайных величин. Математическое ожидание. Дисперсия.
17. Нормальный закон распределения вероятностей.
18. Предмет и методы статистики. Статистическое наблюдение. Сводка и группировка.
19. Средние величины. Свойства средних величин. Структурные средние. Способы определение их для дискретного и интервального рядов. Графический способ.
20. Определение медианы для дискретного и интервального ряда распределения. Определение моды для дискретного и интервального ряда распределения.
21. Показатели вариации ряда наблюдений: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации. Способы расчёта дисперсии. Анализ причин вариации признака.
22. Ряды вариационного дискретного, вариационного интервального, атрибутивного ряда распределения. Примеры интервала группировки, частоты, частости.
23. Статистическое изучение взаимосвязи признаков. Корреляционный и регрессионный анализ.
24. Методы статистики, используемые в криминологических прогнозах.
25. Методы статистики, используемые в изучении факторов распространения преступности.
Приложение. Вариант контрольного задания
1. Для заданных множеств А и В найти АUВ, А∩В, А\В, если А={3, 5, 7}, В={-3, 3, 5,7}, универсальное множество Ω= {-4, -3, 3, 5, 7, 8, 10, 12}.
2. Для заданных множеств А и В найти АUВ, А∩В, А\В, В\А если А={-1, 5}, В={-∞, 1}, универсальное множество Ω= (-∞, +∞).
3. Найти проценты от заданных чисел
a. 2% от 30, 40% от 20, 3% от 70, 14% от 60.
4. Найти число, если
a. 30% его равны 6, 10% его равны 50,
b. 25% его равны 20, 0,3% его равны 0,63.
5. Найти, сколько процентов составляет
a. 9,6 от 48; 3,2 от 1,6; 20 от 40; 128 от 320.
6. На 7 сотрудников выделены 5 путевок. Все путевки различны. Сколькими способами можно их распределить?
7. Сколькими способами можно составить дозор из 3 солдат и 1 офицера, если имеется 80 солдат и 3 офицера?
8. Порядок выступления 8 участников соревнования по стрельбе определяется жребием. Сколько различных исходов жеребьевки при этом возможно?
9. В учебную группу выделили 9 книг, из которых 6 справочников. Найти вероятность того, что среди 5 взятых наугад книг ровно 3 справочника?
10. Среди 100 фотографий есть 1 фотография известного юриста. Взяли наугад 10 фотографий. Какова вероятность того, что среди них есть фотография известного юриста?
11. На баллистическую экспертизу в одной коробке поступили 7 гильз от автомата Калашникова отечественного производства, 5 гильз такого же автомата, но китайского производства и 3 гильзы от автомата польского производства.. Найти вероятность того, что первая наугад вынутая гильза окажется от автомата отечественного производства (событие А1), вторая гильза – китайского производства (событие А2) и третья гильза – польского производства.
12. В районном суде оформлением передачи дел в архив занимаются 2 сотрудника. Первый из них на 1 дело затрачивает 1 час, а второй – 1,5 часа. Каковы средние затраты времени на 1 дело, если общая продолжительность рабочего времени равна?
13. В следственном отделе районного УВД находятся дела о хищении имущества, характеризующиеся следующими данными:
| Число обвиняемых | Число дел |
Определить среднее число обвиняемых на одно уголовное дело, медиану и моду.
14. Изобразите данные таблицы графически несколькими способами.
| Структура уличных преступлений | |
| Вид преступления | Число преступлений |
| Хулиганство | |
| Распространение наркотиков | |
| Убийство, умышленное причинение тяжкого вреда здоровью | |
| Кража | |
| Грабеж, разбой | |
| Прочее |
УЧЕБНОЕ ИЗДАНИЕ
