1. Числовой ряд исследовать на абсолютную и условную сходимость. Для функционального ряда найти область сходимости и исследовать на границе области.
а) 
| б) 
| в)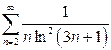  
| |
г) 
| д) 
| ||
а) 
| б) 
| в) 
| |
г) 
| д) 
| ||
а)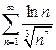 
| б)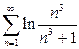 
| в) 
| |
г) 
| д) 
| ||
а) 
| б) 
| в) 
| |
г) 
| д) 
| ||
а) 
| б) 
| в) 
| |
г) 
| д) 
| ||
а) 
| б) 
| в)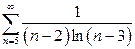 
| |
г) 
| д) 
| ||
а) 
| б)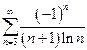 
| в) 
| |
г) 
| д) 
| ||
а) 
| б) 
| в) 
| |
г) 
| д)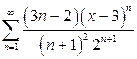 
| ||
а) 
| б) 
| в) 
| |
г) 
| д) 
| ||
а) 
| б) 
| в) 
| |
г) 
| д) 
| ||
а)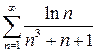 
| б) 
| в) 
| |
г) 
| д)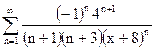 
| ||
а) 
| б)
| в) 
| |
г) 
| д) 
| ||
| а)
| б)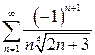 
| в) 
| |
г)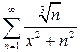 
| д)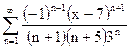 
| ||
а) 
| б) 
| в) 
| |
г) 
| д) 
| ||
а) 
| б) 
| в) 
| |
г) 
| д) 
| ||
а) 
| б) 
| в) 
| |
г) 
| д) 
| ||
а)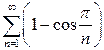 
| б) 
| в)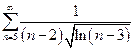 
| |
г) 
| д) 
| ||
а)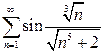 
| б) 
| в) 
| |
г) 
| д) 
| ||
а) 
| б) 
| в)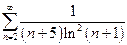 
| |
г) 
| д) 
| ||
а) 
| б) 
| в) 
| |
г) 
| д) 
| ||
а) 
| б) 
| в) 
| |
г) 
| д)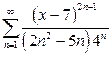 
| ||
а)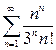 
| б) 
| в) 
| |
г) 
| д) 
| ||
а) 
| б) 
| в) 
| |
г) 
| д) 
| ||
а) 
| б) 
| в) 
| |
г) 
| д)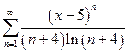 
|
2. Найти сумму ряда.
а) 
| б) 
| |
в) 
| г) 
| |
а) 
| б) 
| |
в) 
| г)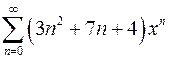 
| |
а) 
| б) 
| |
в) 
| г) 
| |
а)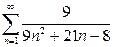 
| б) 
| |
в) 
| г) 
| |
а) 
| б) 
| |
в) 
| г) 
| |
а) 
| б) 
| |
в) 
| г) 
| |
а) 
| б) 
| |
в) 
| г) 
| |
а) 
| б) 
| |
в) 
| г) 
| |
а)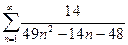 
| б) 
| |
в) 
| г)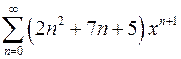 
| |
а) 
| б)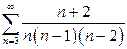 
| |
в) 
| г) 
| |
а) 
| б) 
| |
в)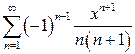 
| г) 
| |
а)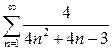 
| б)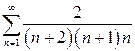 
| |
в) 
| г) 
| |
а) 
| б) 
| |
в) 
| г) 
| |
а) 
| б) 
| |
в) 
| г)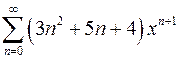 
| |
а)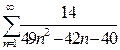 
| б) 
| |
в)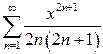 
| г) 
| |
а) 
| б)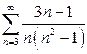 
| |
в) 
| г)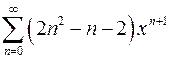 
| |
а) 
| б) 
| |
в) 
| г) 
| |
а) 
| б) 
| |
в) 
| г) 
| |
а) 
| б) 
| |
в) 
| г) 
| |
а) 
| б) 
| |
в) 
| г) 
| |
а) 
| б) 
| |
в) 
| г) 
| |
а)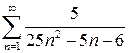 
| б) 
| |
в) 
| г) 
| |
а) 
| б) 
| |
в) 
| г) 
| |
а) 
| б) 
| |
в) 
| г) 
|
3. Найти три первых, отличных от нуля члена разложения в степенной ряд решения 
дифференциального уравнения 
удовлетворяющего начальному условию 
1)  ;
| 
| 2)  ;
| 
|
3)  ;
|
| 4)  ;
|
|
5)  ;
| 
| 6)  ;
|
|
7)  ;
|
| 8)  ;
| 
|
9)  ;
|
| 10)  ;
|
|
11)  ;
| 
| 12)  ;
|
|
13)  ;
| 
| 14)  ;
|
|
15)  ;
|
| 16) ;
| 
|
17)  ;
|
| 18)  ;
|
|
19)  ;
| 
| 20)  ;
|
|
21)  ;
|
| 22)  ;
|
|
23)  ;
|
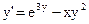| 24)  ;
|
|
Разложить в ряд Фурье функцию на указанном интервале.
1)  ;
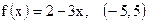| 2) 
|
3)  ; 
|
4) 
|
5)  ;
| 6)  ; 
|
7)  ;
| 8)  ;
|
9)  ;
| 10)  ;
|
11)  ;
| 12)  ;
|
13)  ;
| 14)  ;
|
15)  ; 
| 16)  ;
|
17)  ;
| 18)  ;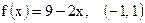
|
19)  ;
| 20)  ;
|
21)  ;
| 22)  ;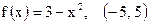
|
23)  ;
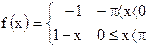| 24) 
|
5. Методом Фурье решить уравнение колебаний конечной струны длины 1 
с граничными условиями 
и начальными условиями 
1) 
| ; 
| ; 
|
2) 
| ; 
| ; 
|
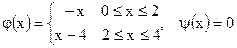
3) 
| ;
| ; 
|
4) 
| ; 
| ; 
|
5) 
| ;
| ; 
|
6) 
| ; 
| ; 
|
| 7)
| ; 
| ; 
|
8) 
|
; 
|
; 
|
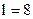
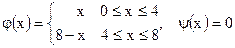
9) 
| ; 
| ; 
|
10) 
| ;
| ;
|
11) 
| ;
| ; 
|
12) 
| ;
| ; 
|
Методом Фурье решить уравнение теплопроводности стержня длины l (найти распределение тепла в любой момент времени t вдоль стержня, имеющего теплопроницаемую боковую поверхность) с граничными условиями.
| 13)
| ;
| ; 
|
14) 
| ;
| ; 
|
| 15)
| ;
| ; 
|
| 16)
| ; 
| ; 
|
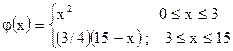
17) 
| ; 
| ; 
|
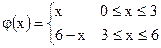
| 18)
| ;
| ; 
|
| 19)
| ; 
| ; 
|
| 20)
| ;
| ; 
|
| 21)
| ; 
| ; 
|
22) 
| ; 
| ; 
|
23) 
| ;
| ; 
|
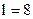
24) 
| ;
| ; 
|
Раздел 8
КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ
Вопросы для самопроверки
1. Задачи, приводящие к криволинейным интегралам. Определение криволинейных интегралов первого и второго рода, их основные свойства и вычисление. Геометрические и механические приложения. Связь между криволинейными интегралами первого и второго рода. Формула Грина.
2. Площадь поверхности. Определение поверхностных интегралов. Их свойства и вычисление.
3. Скалярное поле. Поверхности и линии уровня скалярного поля. Производная по направлению. Градиент скалярного поля, его координатное и инвариантное определения.
4. Векторное поле. Векторные линии и их дифференциальные уравнения.
5. Односторонние и двусторонние поверхности. Поток векторного поля через поверхность. Физический смысл потока в поле скоростей жидкости. Вычисление потока. Теорема Остроградского.
6. Дивергенция векторного поля, ее инвариантное определение и физический смысл. Вычисление дивергенции. Соленоидальные (трубчатые) поля.
7. Линейный интеграл в векторном поле. Работа силового поля. Циркуляция векторного поля. Теорема Стокса. Ротор поля, его координатное и инвариантное определения. Физический смысл ротора в поле скоростей. Условия независимости линейного интеграла от формы пути интегрирования.
8. Потенциальное поле. Условие потенциальности поля. Вычисление линейного интеграла в потенциальном поле.
9. Оператор Гамильтона. Операции второго порядка в векторном анализе. Оператор Лапласа, его выражение в цилиндрических и сферических координатах.
В 
гл. XV §1-2 вводятся понятия криволинейного интеграла первого (по длине дуги) (КИ1) и второго (в координатной форме) (КИ2) рассмотрены их свойства и приложения. Вычисление криволинейных интегралов сводится в общем случае к вычислению определенного интеграла (задача 1,2), доказана формула Грина (§3), Связывающая вычисление КИ2 по замкнутой плоской кривой L с вычислением двойного интеграла по области 
, ограниченной этой кривой
.
Масса дуги материальной кривой при заданной линейной плотности 
вычисляется с помощью КИ1
.
При вычислении циркуляции векторного поля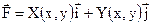 
вдоль плоского контура 
(задача 3) следует применить формулу Грина.
В §5, 6 гл.XV вводятся понятия поверхностных интегралов первого (ПИ1) и второго (ПИ2) рода, доказываются их свойства и приложения. В §7 доказана формула Остроградского-Гаусса, связывающая вычисления ПИ2 от векторного поля
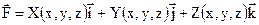
по замкнутой поверхности 
с вычислением тройного интеграла по области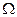 
, ограниченной поверхностью
, где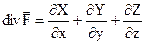 
.
При вычислении ПИ2 по замкнутой поверхности (задача 4), как правило применяют формулу Остроградского.
При решении задачи №5 необходимо вспомнить ( гл. IX §6), что нормаль к поверхности, заданной уравнением 
определяется вектором
.
Производная от функции 
по направлению вектора 
вычисляется ( гл. VIII §14) по формуле
.
Положительным считается направление нормали к поверхности, составляющее острый угол с осью OZ.
Указание. При выполнении контрольной работы №8 приходится вычислять неопределенные (определенные) интегралы вида:
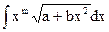, при 
- нечетном удобно сделать замену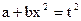 
; при 
- четном либо используют тригонометрическую подстановку, либо интегрируют по частям.
Можно найти аналогичный интеграл (для конкретных значений m, a, b) в книге: Двайт «Таблица интегралов и другие математические формулы».
