Раздел 5
I. Обыкновенные дифференциальные уравнения (ДУ)
I-го порядка.
1.1. Задачи, приводящие к дифференциальным уравнениям. Определения.
Литература: 
, гл. XIII, §1-2, упр. 1,2,4.
1.2. Уравнения с разделяющимися переменными.
Литература: , гл. XIII, §4, упр. 9, 20-26, 35-37.
1.3. Однородные ДУ 1-го порядка и приводящиеся к ним.
Литература: , гл. XIII, §5, упр. 40-47, 55, 56, §6, упр. 48-50.
1.4. Линейные ДУ 1-го порядка и уравнение Бернулли.
Литература: , гл. XIII, §7, упр. 58-63, §8, упр. 66-69.
1.5. Уравнения в полных дифференциалах.
Литература: , гл. XIII, §9, 10, упр. 72-76, 80.
1.6. Огибающая семейства кривых. Особые решения ДУ 1-го порядка.
Литература: , гл. XIII, §11, 12.
Вопросы для самопроверки.
1. Дайте определения:
а) дифференциального уравнения 1-го порядка;
б) общего решения ДУ 1-го порядка;
в) общего интеграла ДУ 1-го порядка;
г) частного решения (интеграла) ДУ 1-го порядка.
2. Сформулируйте задачу Коши для ДУ 1-го порядка и укажите ее геометрический смысл.
3. Дайте определения:
а) интегральной кривой ДУ 1-го порядка;
б) семейства интегральных кривых ДУ, дайте геометрическое толкование ДУ 1-го порядка.
4. Сформулируйте теорему о существовании и единственности решения ДУ 1-го порядка. Что называется особым решением ДУ 1-го порядка?
5. Дайте определения ДУ:
а) с разделенными переменными;
б) с разделяющимися переменными.
Изложите метод нахождения общего решения ДУ с разделяющимися переменными. Найдите общее решение уравнения:
.
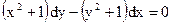6. Дайте определение однородного ДУ 1-го порядка. С помощью какой замены переменной однородное ДУ приводится к уравнению с разделяющимися переменными? Являются ли однородными уравнения:
а)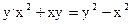 
; б)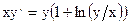 
?
С помощью какой подстановки уравнение вида 
при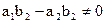 
приводится к однородному?
7. Дайте определение линейного ДУ 1-го порядка: а) однородного; б) неоднородного. Изложите: а) метод Бернулли решения ЛНДУ 1-го порядка; б) метод вариации произвольной постоянной (метод Лагранжа). Является ли уравнение 
линейным относительно функции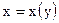 
?
8. Дайте определение уравнения Бернулли. Покажите, что с помощью подстановки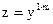 
(где z – новая функция) уравнение Бернулли преобразуется к линейному. Какие методы решения уравнения Бернулли вы знаете?
II. Дифференциальные уравнения высших порядков.
2.1. Общие понятия.
Литература: , гл. XIII, §16, упр. 117.
2.2. Уравнения, допускающие понижение порядка.
Литература: , гл. XIII, §17, упр. 118, 119, §18, упр. 120-124.
2.3. Линейные ДУ 2-го порядка.
Литература: , гл. XIII, §20,21, упр. 129-132, 140-146, §23-25, упр. 149-158, 164-167.
Вопросы для самопроверки.
1. Дайте определения: а) ДУ 2-го порядка; б) его общего и частного решений. Сформулируйте задачу Коши для ДУ 2-го порядка, укажите его геометрический смысл.
2. Изложите методы решений ДУ вида:
а) 
б) 
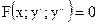в) 
3. Дайте определение: а) линейного ДУ n-го порядка (однородного и неоднородного (ЛОДУ и ЛНДУ)); б) линейно зависимых и линейно независимых функций; в) определителя Вронского; г) фундаментальной системы решений.
Сформулируйте условия линейной независимости решений ЛОДУ. Исследуйте на линейную независимость следующие системы функций: 1) х; lnx; 2) 
; 
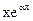; 3) х; х2.
Сформулируйте необходимое условие линейной зависимости системы функций.
4. Сформулируйте терему о структуре общего решения: а) ЛОДУ; б) ЛНДУ.
Докажите, что сумма частных решений уравнений 
и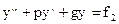 
является решением уравнения 
.
5. Изложите метод Лагранжа вариации произвольных постоянных.
6. Выведите формулу для общего решения линейного однородного ДУ 2 порядка с постоянными коэффициентами в случае действительных различных корней характеристического уравнения.
7. Изложите правило нахождения частного решения линейного ДУ 2 порядка с постоянными коэффициентами и правой частью вида: а)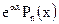 
, где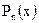 
- многочлен степени 
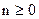; б) 
.
III. Системы обыкновенных дифференциальных уравнений.
Литература: 
гл. ХIII §29 упр. 180, §30 упр. 185, 186, 188, гл.ХХI §17 упр. 14.
Вопросы для самопроверки.
1. Дайте определение: а) нормальной системы ДУ 1 порядка; б) однородной системы в нормальной форме. Сформулируйте задачу Коши для этой системы.
2. Изложите метод исключения решения нормальной системы ДУ 1 порядка.
3. Изложите метод нахождения общего решения нормальной системы 2-х линейных однородных ДУ с постоянными коэффициентами в случае простых корней характеристического уравнения.
4. Запишите в матричной форме нормальную систему и решение нормальной системы 2-х линейных однородных ДУ с постоянными коэффициентами.
Контрольная работа
